こんにちは!しゅんです!
今回は指数分布について解説していきます!
指数分布は確率・統計で登場する数学用語です。この記事では指数分布について図を使って分かりやすく解説していきます。
またこの記事ではpythonを使って指数分布を扱っていこうと思います。
それでは解説していきましょう!
統計検定2級に関する他の記事はこちらから見れます!
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
指数分布ってなに?
ざっくり説明すると指数分布は、ランダムな現象が発生するまでにかかる時間の分布です。例えば地震の発生間隔や製品の寿命などを考えるときに指数分布が使えます。
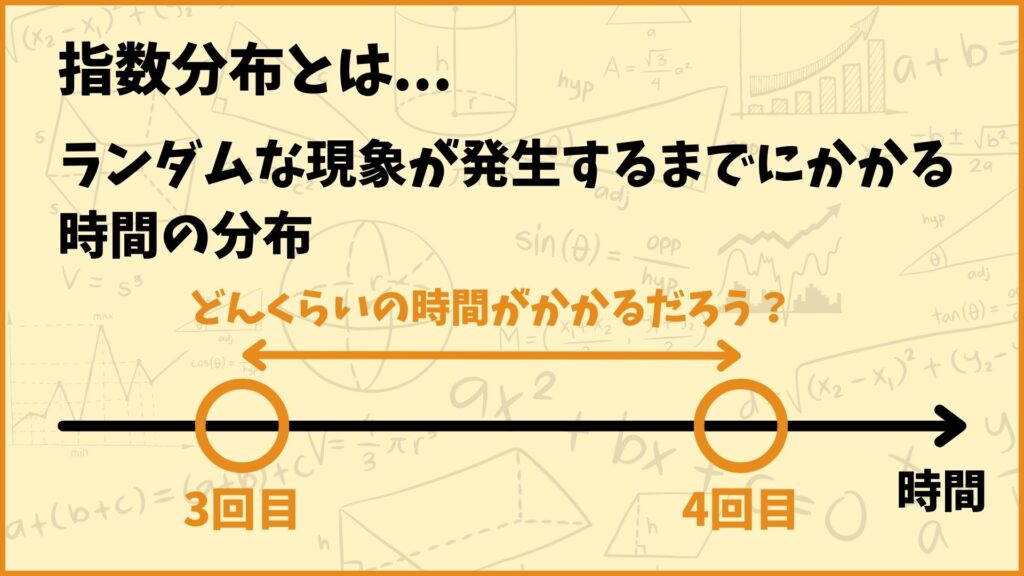
例えば不良品が生産される時間間隔について考えてみたいと思います。とある製品が平均2000時間で故障すると仮定します。例えばこの製品が1500時間以下で故障する確率はいくつになるでしょうか?
結論製品が1500時間以下で故障する確率は約53%になります。なぜこのように計算できるかというと、指数分布の確率密度関数は以下の式で表されるからです。
発生間隔を\(\theta\)とすると
\(f(t) = \frac{1}{\theta} e^{-\frac{t}{\theta}}\)
と表せる。
指数分布は連続型確率分布なので確率密度関数で表しています。
連続型確率分布と確率密度関数はこちらの記事で詳しく解説しています!
この式にさきほどの数値を代入してみます。\(\theta = 2000\)としてこの関数を0から1500まで積分することで確率を求めることができます。
\(\;\; \int_0^{1500} f(t) \, dt\)
=\(\int_0^{1500} \frac{1}{2000} e^{-\frac{t}{2000}} \, dt\)
=\([-e^{-\frac{t}{2000}}]_0^{1500}\)
=\(1 – e^{-\frac{1500}{2000}}\)
=\(0.5276…\)
指数分布とポアソン分布は仲間
指数分布はランダムな現象が発生するまでにかかる時間の分布ですが、これってポアソン分布に似てますよね。
ポアソン分布はこちらの記事で詳しく解説しています!
簡単に説明するとポアソン分布とは一定期間にランダムな現象がどれくらい発生するかという回数が従う分布です。どちらもランダムに発生する現象について考えていますね。
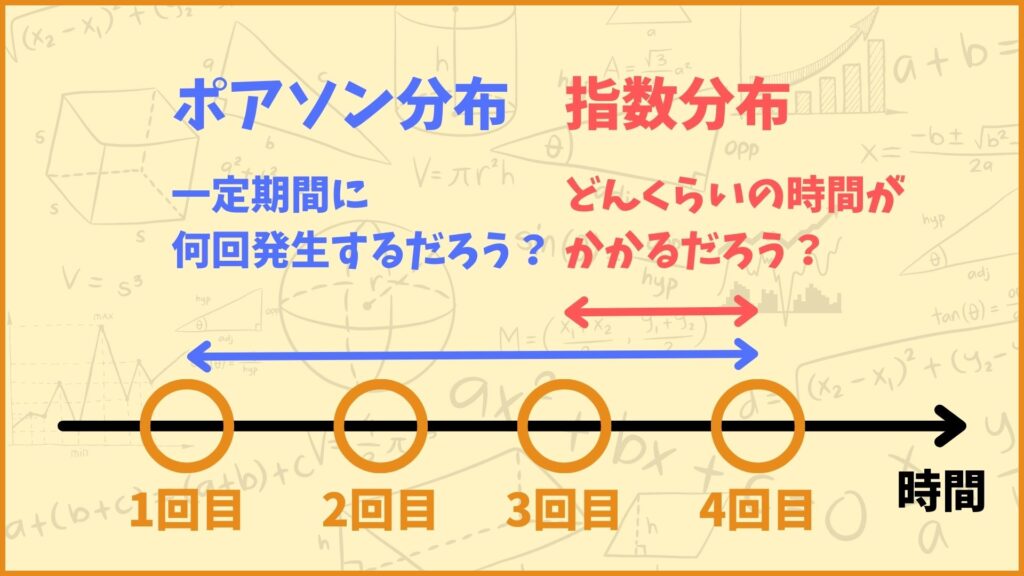
つまり回数に着目したものがポアソン分布で、時間に着目したものが指数分布というわけです。ポアソン分布のパラメータは\(\lambda\)で指数分布のパラメータは\(\theta\)ですが、これらの間には以下のような関係が成り立ちます。
\(\theta=\frac{1}{\lambda}\)
例えば1時間に4回発生する現象の発生間隔は\(\frac{1}{4}\)時間、つまり15分に1回のペースで発生しますねってことです。
\(\lambda\)を使って指数分布の確率密度関数を表すと以下の式になります。
発生回数を\(\lambda\)とすると
\(f(t) = \lambda e^{-\lambda t}\)
と表せる。
ということでここからは\(\lambda\)を使って説明したいと思います。
指数分布の期待値と分散
指数分布の期待値と分散は下のようになります。
期待値 : \(\mu = \frac{1}{\lambda}\)
分散 : \(\sigma^2 = \frac{1}{\lambda^2}\)
期待値はその確率分布が取る値の平均を表します。例えば1時間を基準にして\(\lambda=5\)のとき、発生間隔は平均\(\frac{1}{5}\)時間、つまり12分になるということを表しています。分散はその確率分布が取る値にどれだけばらつきがあるかを表します。
指数分布をpythonで扱う
最後にpythonを使って指数分布を扱いたいと思います。プログラミングの知識が必要なので、分からなければプログラムの所は飛ばして結果だけ確認してみてください。
事前準備
pythonで確率・統計を扱うときはscipyというライブラリをよく使います。その中でも今回は指数分布を扱いたいのでexponをインポートします。exponは指数分布(exponential distribution)のことです。また数値計算でよく使うnumpy、グラフ作成でよく使うmatplotlibというライブラリもインポートしておきます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import expon
import scipy.stats as stats指数分布の確率を計算する
ということでまずは\(\lambda=\frac{1}{2000}\)として指数分布の確率を計算します。例えば確率変数\(X\)が0から1500の間にある確率を求めてみましょう。指数分布は連続型確率関数なので確率を面積で求めます。
# パラメータ λ を計算
lambda_param = 2000
# 累積分布関数(CDF)を計算
probability = expon.cdf(1500, scale=lambda_param)
print("1500以下になる確率:", probability)
これは、平均2000時間に1回発生する現象が1500時間以下で発生する確率を計算しています。 \(\theta=2000\)なので\(\lambda=\frac{1}{2000}\)となります。累積分布関数は数字を指定すると0から指定した数字までの面積を計算します。
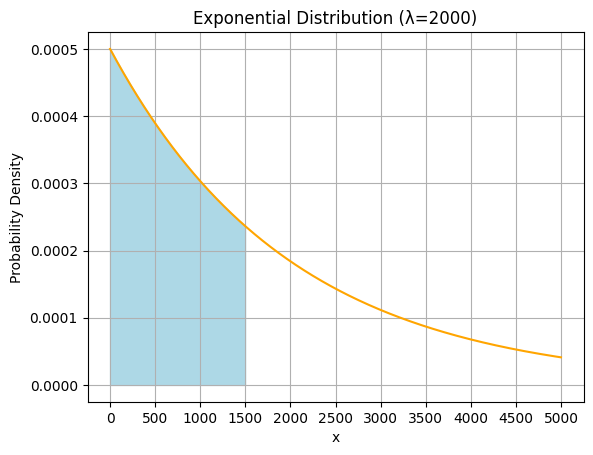
上図のオレンジ線が指数分布の確率密度関数で、青い部分が0から1500の間になる確率です。上のプログラムはこの青い範囲の面積を求めているというわけです。
指数分布の確率密度関数をグラフ化する
指数分布の確率密度関数をグラフ化してみましょう。\(\lambda=\frac{1}{2000}\)としてグラフを描いてみます。
lambda_val = 1/2000 # ラムダの値を設定
x = np.linspace(0, 5000, 1000) # 0から1500までの範囲を1000点で区切る
exponential_dist = expon(scale=1/lambda_val) # 指数分布を表現するオブジェクトを作成
pdf = exponential_dist.pdf(x) # 確率密度関数(PDF)を計算
plt.plot(x, pdf, color="orange") # PDFをプロット
plt.xlabel("x")
plt.ylabel("Probability Density")
plt.title("Exponential Distribution (λ=2000)")
plt.xticks(np.arange(0,5001,500))
plt.grid(True)
plt.show()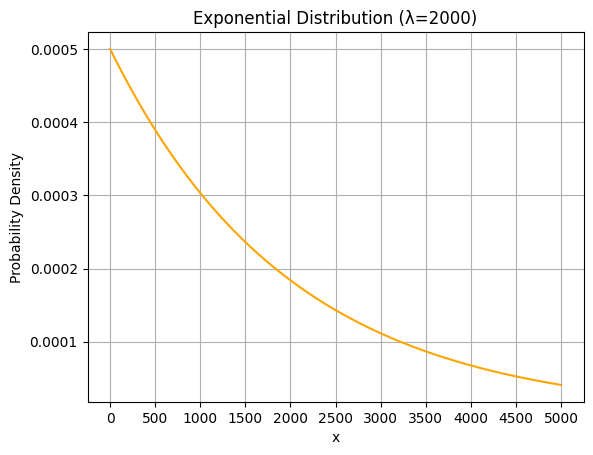
指数分布の累積分布関数をグラフ化する
指数分布の累積分布関数をグラフ化してみましょう。\(\lambda=\frac{1}{2000}\)としてグラフを描いてみます。
lambda_val = 1/2000 # ラムダの値を設定
x = np.linspace(0, 5000, 1000) # 0から1500までの範囲を1000点で区切る
exponential_dist = expon(scale=1/lambda_val) # 指数分布を表現するオブジェクトを作成
cdf = exponential_dist.cdf(x) # 確率密度関数(PDF)を計算
plt.plot(x, cdf, color="orange") # CDFをプロット
plt.xlabel("x")
plt.ylabel("Probability Density")
plt.title("Exponential Distribution (λ=2000)")
plt.xticks(np.arange(0,5001,500))
plt.yticks(np.arange(0,1.1,0.1))
plt.grid(True)
plt.show()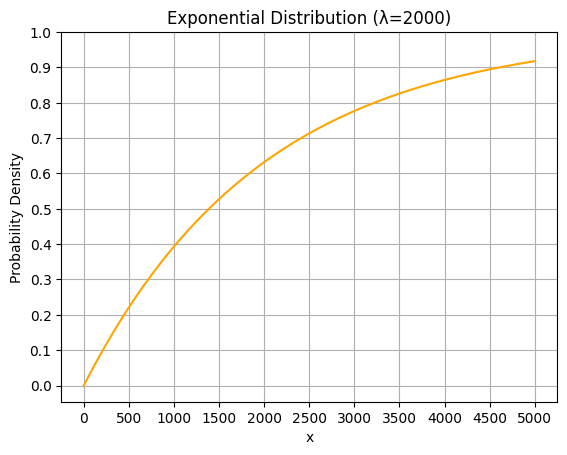
おわりに
いかがでしたか。
今回の記事では指数分布について解説していきました。
今後もこのような経営工学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。