こんにちは!しゅんです!
割当問題を簡単に説明すると、例えば10人の従業員を10個の仕事に割り当てるときにどのように割り当てたら効率的になるかを考える問題です。
今回の記事では割当問題の中でも
「1日でやる仕事数に上限がある場合の割当問題」
をpythonで解いてみたいと思います。それではやっていきましょう!
「従業員に余りが出る場合の割当問題」
「従業員が複数の仕事を担当できる場合の割当問題」
「時間帯によって異なる仕事を行う場合の割当問題」
「1日でやる仕事数に上限がある場合の割当問題」
「最も負担がかかる従業員の負担を最小にする割当問題」
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
今回解く問題
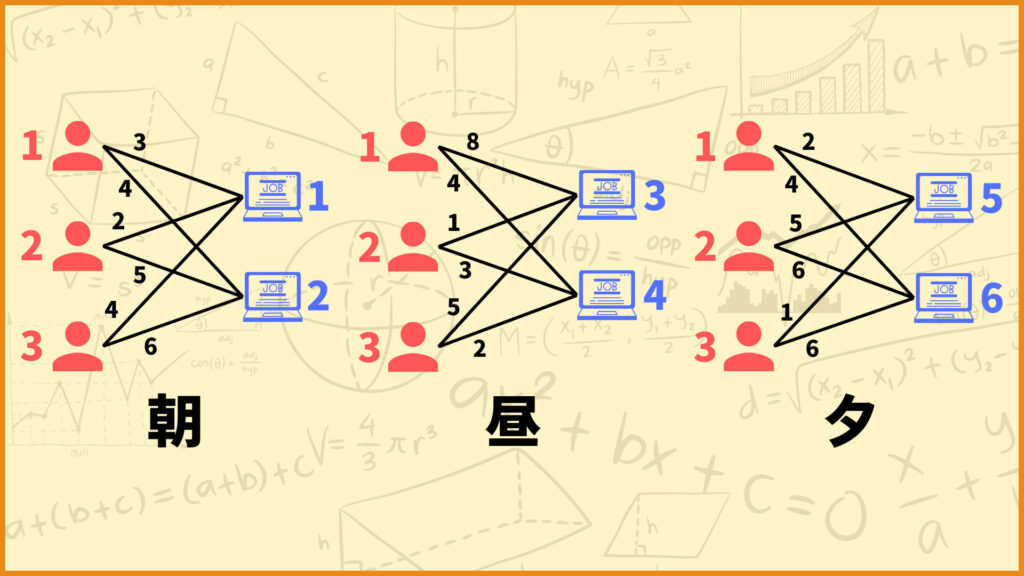
今回は3人の従業員に6個の仕事を割り当てることを考えます。6個の仕事は朝、昼、夕の3つの時間帯で分けられていて、朝に仕事1,2、昼に仕事3,4、夕に仕事5,6を行います。
各時間帯において各従業員は最大1つの仕事が割り当てられ、各仕事は必ず1人の従業員に割り当てられます。各辺には重みがあります。ごちゃごちゃするので図では省略しています。
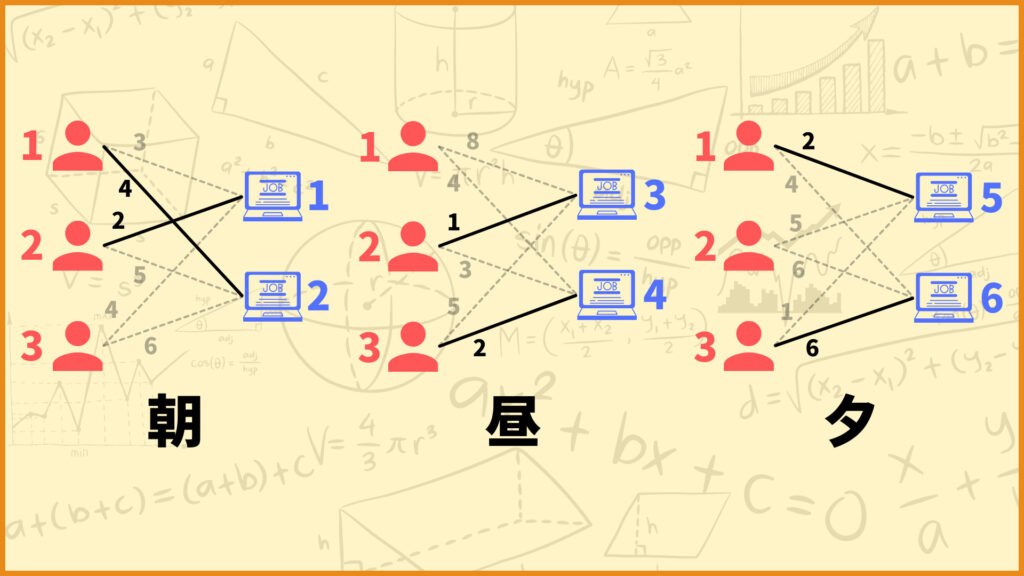
上図の例で言うと、朝は「従業員1が仕事2、従業員2が仕事1」を担当し、昼は「従業員2が仕事3、従業員3が仕事4」を担当し、夕は「従業員1が仕事2、従業員3が仕事6」を担当します。
これに加えて今回は「各従業員が1日でできる仕事数は最大2つまで」という制約を考えます。
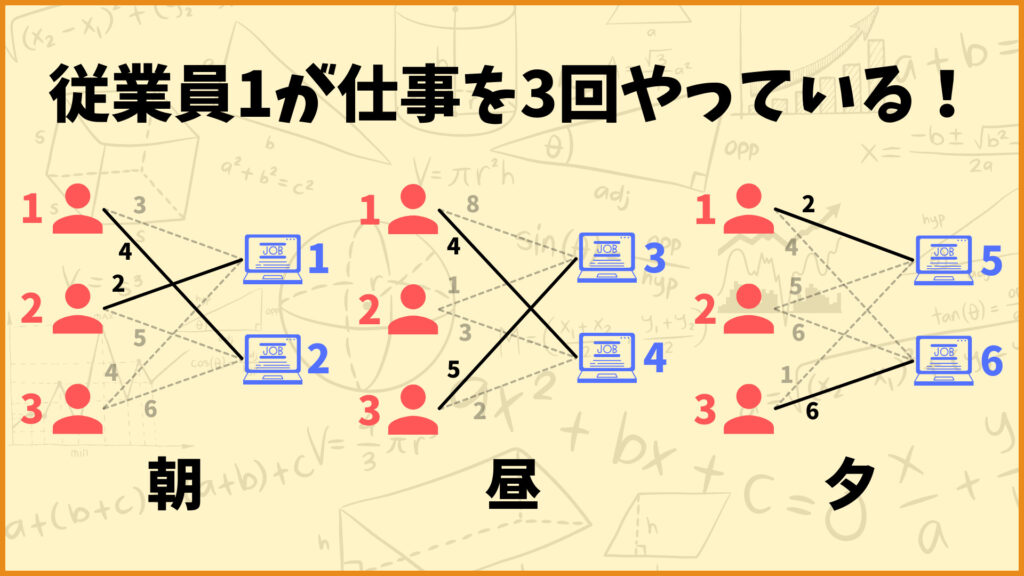
例えば上のような割当を見てみると、従業員1が仕事を3回やっていますね。これは「各従業員が1日でできる仕事数は最大2つまで」と言う制約に反しているので、ダメな割当とします。
今回はこのような割当の中で、重みの合計が最小となるような割当を求める問題を整数計画問題として定式化してみたいと思います。
整数計画問題として定式化したものをpythonで実装する
この割当問題を整数計画問題として定式化したものを、pythonで実装したいと思います。前回の記事で上の問題を整数計画問題として定式化する方法は解説しているので、ここでは結果だけ載せておきます。
・パラメータ
\(T = \{1,2,3\}\):時間帯の集合
\(E = \{1,2,3\}\) : 従業員の集合
\(J_1 = \{1,2\}\) : 朝の仕事の集合
\(J_2 = \{3,4\}\) : 昼の仕事の集合
\(J_3 = \{5,6\}\) : 夕の仕事の集合
\(w_{ij}\) : 辺\((i,j)\)の重み
・変数
\(x_{ijt} \in \{0,1\} \;\; (\forall t \in T, \forall i \in E, \forall j \in J_t)\)
整数計画問題として定式化:
\(\min \;\;\; \sum\limits_{t \in T}\sum\limits_{i \in E}\sum\limits_{j \in J_t} w_{ij}x_{ijt}\)
\(\;\text{s.t.}\;\;\;\sum\limits_{j \in J_t} x_{ijt} \leq 1 \;\;\;\; (\forall t \in T, \forall i \in E)\)
\(\;\;\;\;\;\;\;\;\;\;\sum\limits_{i \in E} x_{ijt}=1 \;\;\;\; (\forall t \in T, \forall j \in J_t)\)
\(\;\;\;\;\;\;\;\;\;\;\sum\limits_{t \in T}\sum\limits_{j \in J_t} x_{ijt} \leq 2 \;\;\;\; (\forall i \in E)\)
\(\;\;\;\;\;\;\;\;\; x_{ijt} \in \{0,1\} \;\;(\forall t \in T, \forall i \in E, \forall j \in J_t)\)
「時間帯によって異なる仕事を行う場合の割当問題」を整数計画問題として定式化する記事はこちらから!
コードの全貌と実行結果
まず最初にコードの全貌と実行結果を示してから、コードと結果について1つずつ解説していきたいと思います。コードの全貌は以下のようになります。
## 事前準備
!pip install pulp # pulpをインストール
from pulp import * # pulpをインポート
## パラメータの設定
T = [1,2,3]
E = [1,2,3] # 従業員側の頂点を設定
J = [[1,2],[3,4],[5,6]] # 仕事側の頂点を設定
# 各辺の重みを設定(辞書)
w = {(1,1):3,(1,2):4,
(1,3):8,(1,4):4,
(1,5):2,(1,6):4,
(2,1):2,(2,2):5,
(2,3):1,(2,4):3,
(2,5):5,(2,6):6,
(3,1):4,(3,2):6,
(3,3):5,(3,4):2,
(3,5):1,(3,6):6,}
## 整数計画問題の設定
prob = pulp.LpProblem(sense = LpMinimize) # 問題をMinimizeに設定
x = LpVariable.dicts("x",((i,j,t)for t in T for i in E for j in J[t-1]), cat = "Binary") # 0-1変数の設定
prob += lpSum(x[i,j,t] * w[(i,j)] for t in T for i in E for j in J[t-1]) # 目的関数の設定
for t in T:
for i in E:
prob += lpSum(x[i,j,t] for j in J[t-1]) <= 1 # 従業員側の頂点に関する制約条件を設定
for t in T:
for j in J[t-1]:
prob += lpSum(x[i,j,t] for i in E) == 1 # 仕事側の頂点に関する制約条件を設定
for i in E:
prob += lpSum(x[i,j,t] for t in T for j in J[t-1]) <= 2
result = prob.solve() # 問題を解く
## 結果の表示
print(LpStatus[result]) # 得られた結果の状態を表示(Optimalなら最適解が得られている)
for t in T:
for i in E:
for j in J[t-1]:
if x[i,j,t].value() == 1:
print(f"x{i}{j}{t} =",x[i,j,t].value()) # 最適解(変数の値が1のものだけ)を表示
print("最適値 :", prob.objective.value()) # 最適値を表示このコードを実行すると以下のような結果が得られました。

それでは1つずつ解説していきます。
コードを1つずつ解説する
事前準備
## 事前準備
!pip install pulp # pulpをインストール
from pulp import * # pulpをインポート問題を解くための事前準備としてpulpをインポートします。pulpはpythonで数理最適化の問題を解くために使うライブラリです。pulpをインストールしてからインポートしています。
パラメータの設定
## パラメータの設定
T = [1,2,3]
E = [1,2,3] # 従業員側の頂点を設定
J = [[1,2],[3,4],[5,6]] # 仕事側の頂点を設定
# 各辺の重みを設定(辞書)
w = {(1,1):3,(1,2):4,
(1,3):8,(1,4):4,
(1,5):2,(1,6):4,
(2,1):2,(2,2):5,
(2,3):1,(2,4):3,
(2,5):5,(2,6):6,
(3,1):4,(3,2):6,
(3,3):5,(3,4):2,
(3,5):1,(3,6):6,}次に各パラメータを設定していきます。今回は完全2部グラフを考えているので頂点と各辺の重みを設定するだけでOKです。
Tが時間帯の集合、Eが従業員側の頂点、Jが仕事側の頂点を表しています。Jは2次元リストにしています。
wは各辺の重さを辞書形式で表しています。例えばw[(1,6)]=4ですが、これは辺\((1,6)\)の重みが4であることを表しています。つまり従業員1の仕事6に対する仕事やりたくない度は4であることを表しています。
整数計画問題の設定
## 整数計画問題の設定
prob = pulp.LpProblem(sense = LpMinimize) # 問題をMinimizeに設定
x = LpVariable.dicts("x",((i,j,t)for t in T for i in E for j in J[t-1]), cat = "Binary") # 0-1変数の設定
prob += lpSum(x[i,j,t] * w[(i,j)] for t in T for i in E for j in J[t-1]) # 目的関数の設定
for t in T:
for i in E:
prob += lpSum(x[i,j,t] for j in J[t-1]) <= 1 # 従業員側の頂点に関する制約条件を設定
for t in T:
for j in J[t-1]:
prob += lpSum(x[i,j,t] for i in E) == 1 # 仕事側の頂点に関する制約条件を設定
for i in E:
prob += lpSum(x[i,j,t] for t in T for j in J[t-1]) <= 2
result = prob.solve() # 問題を解く
それではいよいよ整数計画問題をpythonで記述していきたいと思います。少し長いのでさらにいくつかのパートに分けて説明したいと思います。
問題をMinimizeに設定
prob = pulp.LpProblem(sense = LpMinimize) # 問題をMinimizeに設定この行では問題の種類を設定しています。pulp.LpProblemで数理最適化の問題を作ることができます。かっこの中のsense=の所で問題の種類を設定できます。今回は最小値を求めたいのでLpMinimizeと設定します。
最大値を求めたい場合はLpMaximizeとします。
0-1変数の設定
x = LpVariable.dicts("x",((i,j,t)for t in T for i in E for j in J[t-1]), cat = "Binary") # 0-1変数の設定
次に0-1変数\(x_{ij}\in\{0,1\}\)を設定しています。変数はLpVariableで設定できます。変数をたくさん作りたい場合は.dictを使うと便利です。かっこの中は左から順番に(”変数の名前” 添字の集合, cat=”変数の種類”)を表しています。
上の例で言うと名前はx、添字の集合は従業員の集合Eと仕事の集合Jと時間帯の集合T、変数はBinary(0-1変数)と設定しています。
Jが2次元リストなので添字の集合をそのまま(E, J, T)としてもうまくいきません。またpythonのリストのインデックスは0から始まるのでJ[t-1]にして揃えています。
Binary : 0-1変数
Integer : 整数変数
Continuous : 連続変数
目的関数の設定
prob += lpSum(x[i,j,t] * w[(i,j)] for t in T for i in E for j in J[t-1]) # 目的関数の設定これは本筋ではありませんが、目的関数と制約条件はprob+=を最初に付けます。probは問題をMinimizeに設定したときにprob=としたのでそれに合わせます。もしMinimizeの設定の所で
problem = pulp.LpProblem(sense = LpMinimize) # 問題をMinimizeに設定と書いたら目的関数と制約条件の設定の所ではproblem+=と書く必要があります。
肝心の目的関数の設定についてですが、\(\sum\limits w_{ij}x_{ijt}\)を表すにはlpSumが便利です。イメージ的にはlpSumが\(\sum\)の役割をしてくれると思ってください。
for t in T for i in E for j in J[t-1]と書くことで\(\sum\limits_{t \in T}\sum\limits_{i \in E}\sum\limits_{j \in J}\)を表現することができます。
制約条件の設定
for t in T:
for i in E:
prob += lpSum(x[i,j,t] for j in J[t-1]) <= 1 # 従業員側の頂点に関する制約条件を設定
for t in T:
for j in J[t-1]:
prob += lpSum(x[i,j,t] for i in E) == 1 # 仕事側の頂点に関する制約条件を設定
for i in E:
prob += lpSum(x[i,j,t] for t in T for j in J[t-1]) <= 2 # 従業員と時間帯に関する制約条件を設定
次に制約条件を設定していきます。まず従業員側の頂点に関する制約
\(\sum\limits_{j \in J_t}x_{ij} = 1 \;\; (\forall t \in T, \forall i \in E)\)
を設定します。先ほどと同じように\(\sum\)はlpSumで表現します。かっこの中を(x[i,j] for j in J[t-1])とすることで\(\sum\limits_{j \in J_t}x_{ij}\)を表現することができます。
これでが1になれば良いので== 1としています。
= 1にするとエラーが出るので気を付けてください。
仕事側の頂点に対しても同じように制約条件を設定します。
従業員と時間帯に関する制約は
\(\sum\limits_{t \in T}\sum\limits_{j \in J_t} x_{ijt} \leq 2 \)
です。\(\sum\)をlpSumで表現し、かっこの中を(x[i,j,t] for t in T for j in J[t-1])とすることで
\(\sum\limits_{t \in T}\sum\limits_{j \in J_t}\)を表現できます。
これが2以下になれば良いので<= 2としています。
問題を解く
result = prob.solve() # 問題を解く
prob.solve()で問題を解くことができます。結果をresultに格納しておきます。
結果の表示
## 結果の表示
print(LpStatus[result]) # 得られた結果の状態を表示(Optimalなら最適解が得られている)
for t in T:
for i in E:
for j in J[t-1]:
if x[i,j,t].value() == 1:
print(f"x{i}{j}{t} =",x[i,j,t].value()) # 最適解(変数の値が1のものだけ)を表示
print("最適値 :", prob.objective.value()) # 最適値を表示
最後に結果を表示するコードについて説明したいと思います。まずprint(LpStatus[result])で得られた結果の状態を表示します。もしOptimalと返されたらちゃんと最適値が求まっています。
次に最適解、すなわち\(x_{ijt}=1\)を満たす変数\(x_{ijt}\)を表示するように設定します。解の値は.value()で得ることができます。
今回は\(i=1,2,3 \;j=1,2,…,6\)に対して\(x_{ij}=1\)の変数だけ表示したいので、for t in T: for i in E: for j in J[t-1]:でiとjとtを回して、if x[i,j,t].value() == 1:で\(x_{ijt}=1\)のものだけ取り出しています。
最後に最適値を表示するように設定します。最適値はobject.value()で得ることができます。
結果を1つずつ解釈する
上のコードを実行したら以下の結果が出力されたので、この結果を1つずつ解釈していきましょう。

1行目は無視して大丈夫です。(pulpが既にインストールされていることを表しています。)
2行目は結果の状態を表しています。Optimalと表示されているのでちゃんと最適解が得られていることが分かりますね。
3行目~8行目では最適解(変数の値が1のものだけ)を表しています。これを見るとx121、x211、x232、x342、x163、x353が1であることが分かります。
これはつまり
朝は従業員1が仕事2、従業員2が仕事1を担当し、
昼は従業員2が仕事3、従業員3が仕事4を担当し、
夕は従業員1が仕事6、従業員3が仕事5を担当する
のが最適な割当だということを表しています。
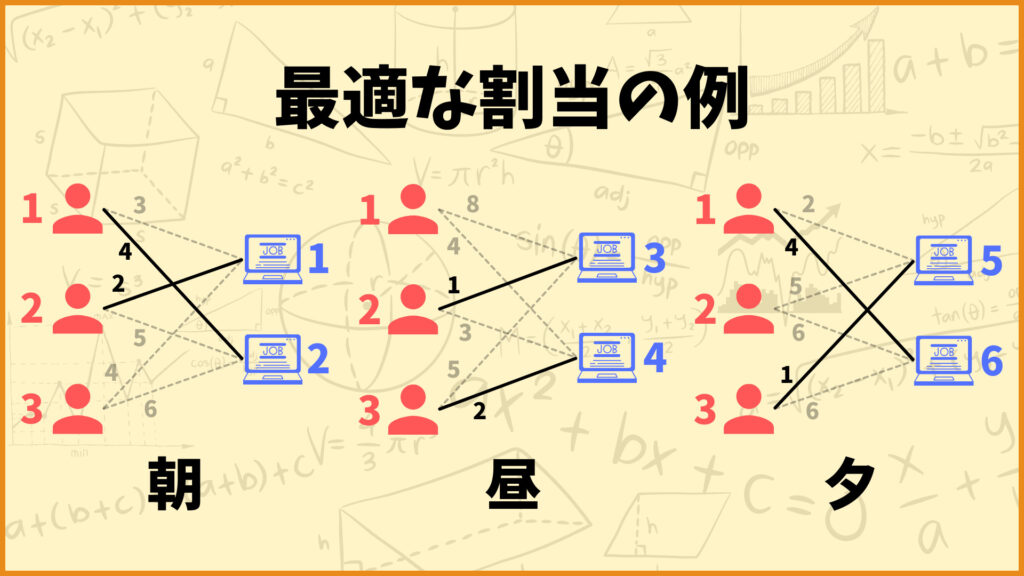
ちゃんと全ての従業員の仕事をやる回数が2回以下になっています。
9行目は最適値を表しています。これを見ると今回の問題の最適値は14であることが分かりますね。
おわりに
いかがでしたか。
今回の記事では割当問題について解説していきました。
今後もこのような組合せ最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。









