- 割当問題ってなに?
- 具体例を使って割当問題を理解したい…
- 割当問題を整数計画問題として定式化したい…
こんにちは!しゅんです!
今回の記事では割当問題ついて解説していきます!
この記事では割当問題を整数計画問題として定式化する方法を解説し、次回の記事では割当問題をpythonで解く方法を解説しています。
また別の記事では割当問題を解くアルゴリズムである、ハンガリー法(ハンガリアン法)の手順について解説しています!
また別の記事では焼きなまし法を使って割当問題を解く方法を解説しています!
例えば10人の従業員を10個の仕事に割り当てる場合に、どのように割り当てたら効率的なのかを考えるのが割当問題です。従業員1は仕事4が得意だけど、逆に従業員3は仕事2が苦手みたいなことはよくあります。
この記事では割当問題を整数計画問題として定式化する方法について解説したいと思います。
それではやっていきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
具体例を使って考える
4人の従業員と4つの仕事
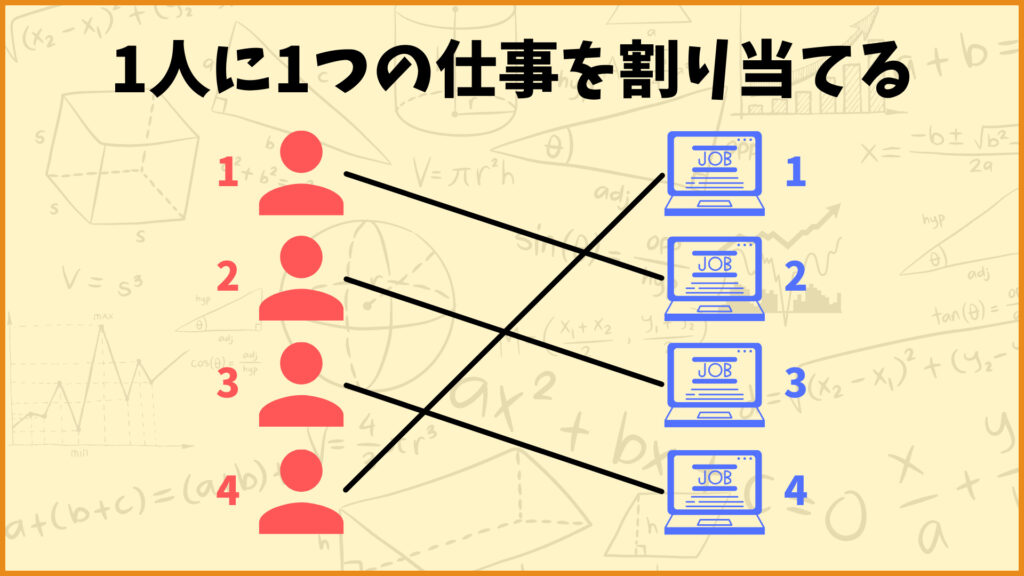
割当問題の具体例として従業員に仕事を割り当てる問題を考えます。今自分がある会社の社長で、4人の従業員を4つの仕事に割り当てることを考えます。
このとき各従業員は必ず1つ仕事を担当し、各従業員が行う仕事が被らないように割り当てます。
上の図の例で言うと従業員1が仕事2、従業員2が仕事3、従業員3が仕事4、従業員4が仕事1を担当しています。では上の条件を満たせばどんな割り当て方でも良いのかというと、そうはいきません。
人にはやりたい仕事とやりたくない仕事がある
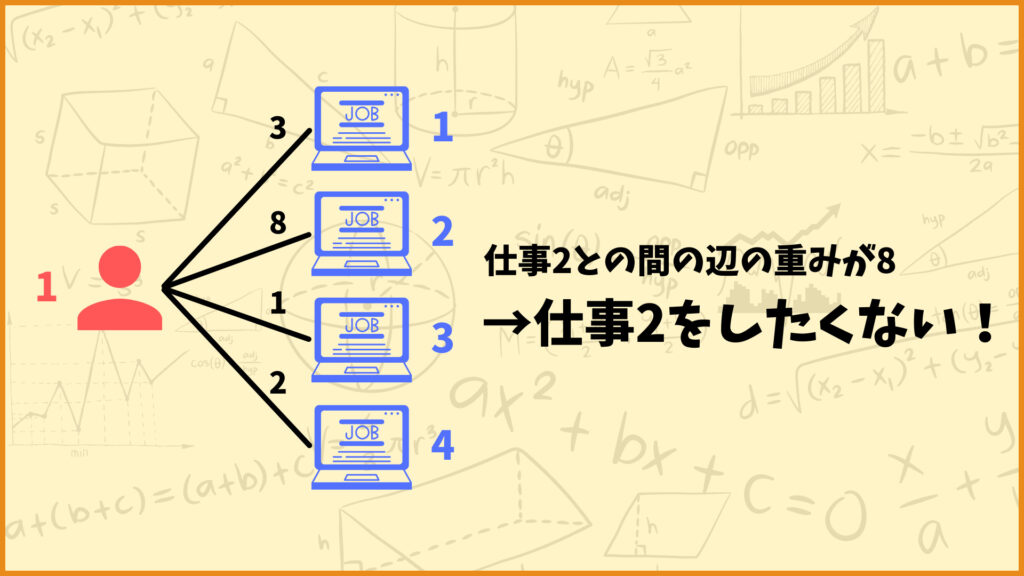
各従業員はどの仕事がしたいか、またどの仕事をしたくないかという好みがあります。会社としても効率的に仕事をしてもらうために、各従業員にはなるべく自分が好きな仕事をやってもらった方が良いですよね。
ということで各従業員がその仕事をどれくらいやりたいかを数字で表します。
今回は数が小さい程その仕事をやりたい、また数が大きい程その仕事をやりたくないと考えます。
上の図で言うと従業員1の仕事やりたくない度は仕事1が3、仕事2が8、仕事3が1、仕事4が2です。そのため従業員1は仕事2を全然やりたくないということが分かります。
逆に言うと従業員1にはなるべく仕事3を当てた方が良いということも分かります。
全員の要望に応えることができない場合がある
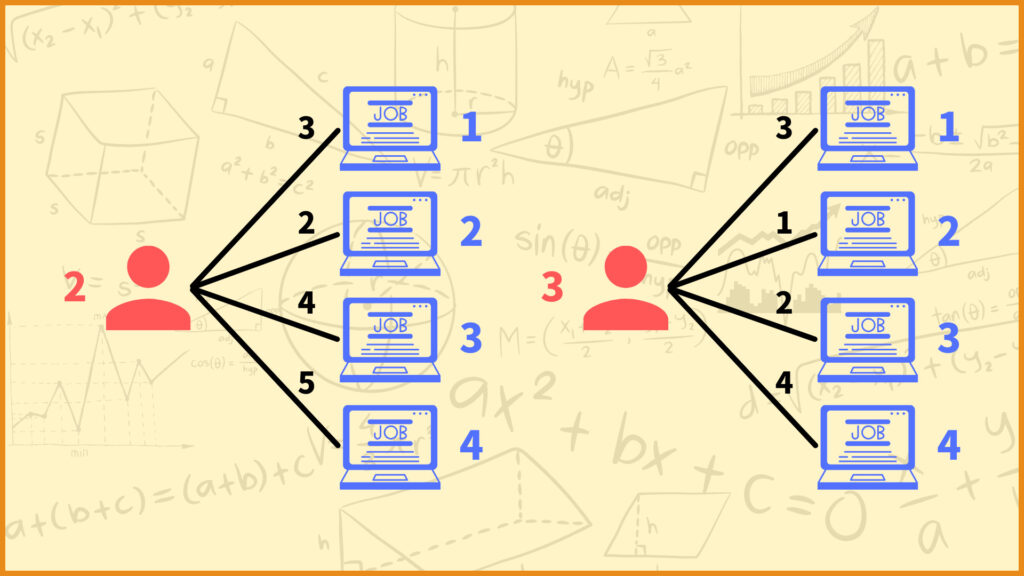
同じように従業員2,3についても考えてみると、従業員2も従業員3も仕事2を一番やりたいということが分かります。しかしここで1つ問題が生じてしまいます。それは
仕事は1人にしか割り当てられない
ということです。つまり従業員2に仕事2を割り当ててしまうと従業員3には仕事2を割り当てることができなくなります。一番やりたい仕事が被っている場合は従業員全員に第一希望の仕事を割り当てることができません。
このようなことは現実世界でもよくありますね。
全員の要望になるべく応えるにはどうすれば良いか
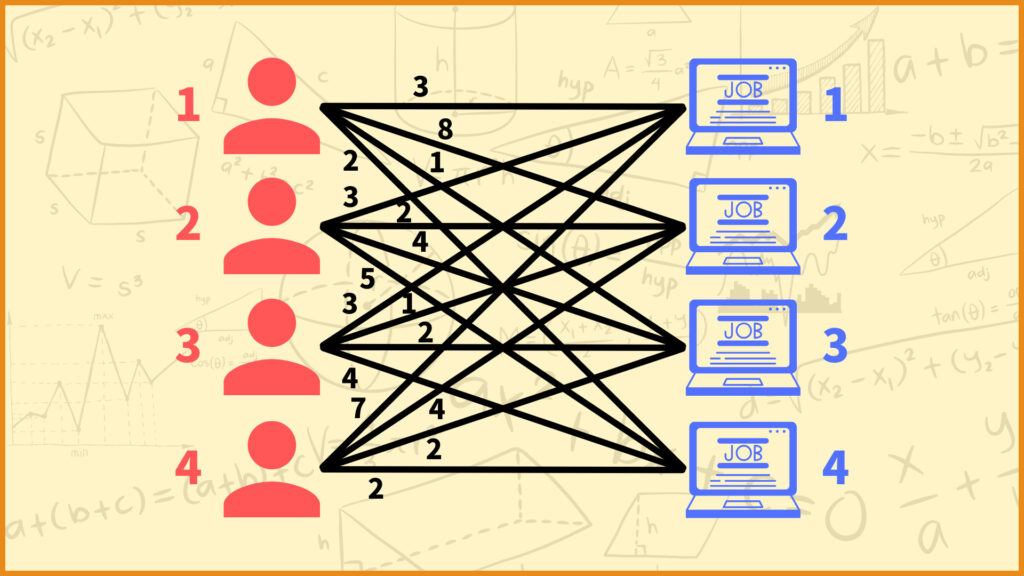
ということで全ての従業員に対して各仕事へのやりたくない度を書いてみました。これまで話したことからわかるように、全員の第一希望を通すことはできません。そこで今回は
「従業員全員のやりたくない度の合計を最小にする」
ということを考えます。こう考えることで従業員の要望をなるべく実現し、かつ1人の従業員が1つの仕事を担当するような割当を作ることができます。
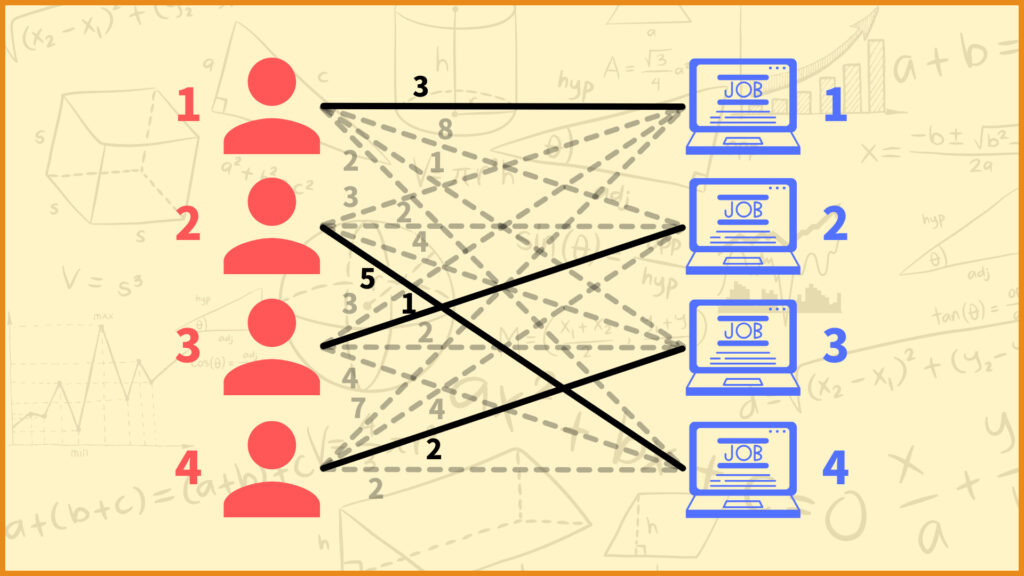
例えば上図のように従業員1に仕事1、従業員2に仕事4、従業員3に仕事2、従業員4に仕事3を割り当てる場合を考えます。このときのやりたくない度の合計は
\(3+5+1+2=11\)
となります。
完全2部グラフの最小重み完全マッチングとして考えられる
ここまで割当問題について解説していきましたが、これってよく見ると完全2部グラフの最小重み完全マッチング問題と同じになっています。
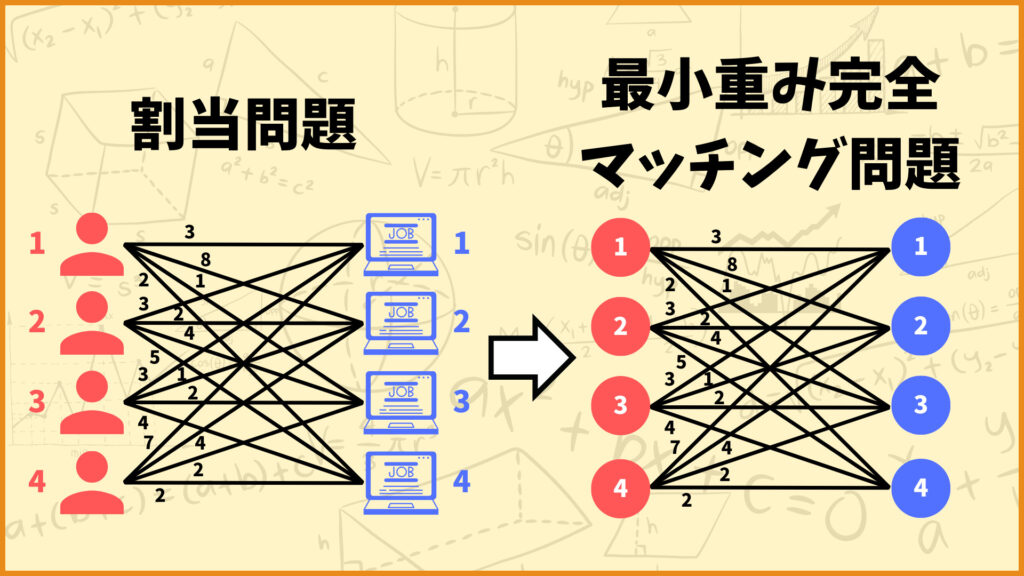
従業員を左側の頂点、仕事を右側の頂点、従業員 \(i\) の仕事 \(j\) に対する仕事やりたくない度を辺 \((i,j)\) の重み \(w_{ij}\) と考えると、この割当問題は2部グラフの最小重み完全マッチング問題と考えることができます。
最小重み完全マッチング問題を整数計画問題として定式化する方法については過去の記事で詳しく解説しているので、その説明に沿って定式化について説明したいと思います。
割当問題を整数計画問題として定式化する

それでは上の割当問題を整数計画問題として定式化してみましょう。とは言っても最小重み完全マッチング問題を整数計画問題として定式化するのと同じようにすればOKです。
という訳で、「パラメータ・変数」、「目的関数」、「制約条件」の3つについて考えてみましょう。
パラメータ、変数の設定
パラメータ
\(w_{ij}\):辺 \((i,j)\) の重み
変数
\(x_{ij}\in\{0,1\}\):辺 \((i,j)\) を採用するなら1、そうでないなら0を取る0-1変数
パラメータとして辺の重み \(w_{ij}\)、変数として \(x_{ij}\) を用意します。
\(w_{ij}\) は辺 \((i,j)\) の重みを表します。(\(w_{ij}\) は従業員 \(i\) の仕事 \(j\) に対する仕事やりたくない度と考えてください。)例えば辺 \((1,2)\) の重みは\(8\)なので
\(w_{12} = 8\)
となります。
変数 \(x_{ij}\) は辺 \((i,j)\) を採用するなら1、そうでないなら0となる変数です。(従業員 \(i\) に仕事 \(j\) が割り当てられるなら1、そうでないなら0と考えてください。)
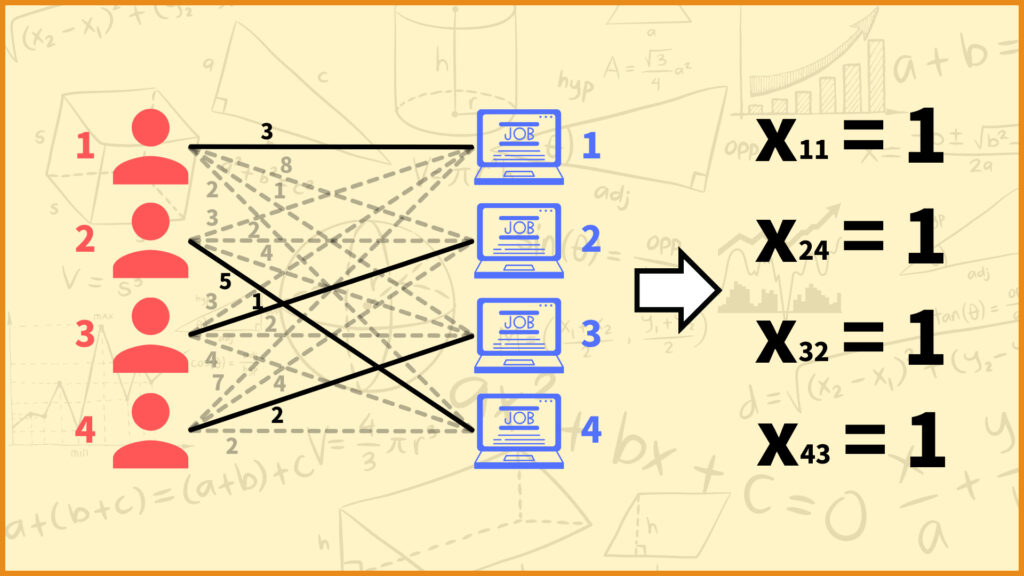
例えば上の例で言うと従業員1に仕事1、従業員2に仕事4、従業員3に仕事2、従業員4に仕事3が割り当てられているので、
\(x_{11}=x_{24}=x_{32}=x_{43}=1\)
となり、その他の変数は0を取ります。
目的関数の設定
次に目的関数を設定しましょう。
\( \sum\limits_{i=1}^4\sum\limits_{j=1}^4 w_{ij}x_{ij}\)
目的関数は
「従業員全員のやりたくない度の合計を最小にする」
なので、やりたくない度\(w_{ij}\)に変数\(x_{ij}\)を掛け算して全部足したものを目的関数とします。
例えばさっきの例で言うと
\(x_{11}=x_{24}=x_{32}=x_{43} = 1\)
でそれ以外の変数が\(0\)になるので、結局目的関数は
\(\sum\limits_{i=1}^4\sum\limits_{j=1}^4 w_{ij}x_{ij}=w_{11}+w_{24}+w_{32}+w_{43}\)
となります。
制約条件の設定
従業員側の制約:
\(\sum\limits_{j=1}^4 x_{ij}=1 \;\;\;\; (i = 1,2,3,4)\)
仕事側の制約:
\(\sum\limits_{i=1}^4 x_{ij}=1 \;\;\;\; (j = 1,2,3,4)\)
従業員側の制約については、各従業員には必ず1つの仕事が割り当てられるということを表しています。例えば従業員1(\(i=1\))に関する制約を見てみると
\(\sum\limits_{j=1}^4 x_{1j}=x_{11}+x_{12}+x_{13}+x_{14} = 1\)
となっています。
例えば\(x_{12} = 1\)(従業員1に仕事2が割り当てられる)だと、自動的に\(x_{11}=x_{13}=x_{14}=0\)となり、これは従業員1には仕事1,3,4が割り当てられないと言うことを表しています。
このように変数のうちどれか1つが1になったら他が全て0になるのがこの制約です。この制約を\(i=2,3,4\)に対しても課したいので\((i=1,2,3,4)\)となっています。
仕事側の制約に関しても従業員側の制約と同じように、各仕事には必ず1人の従業員が割り当てられるということを表しています。
整数計画問題としてまとめる
最後にこれらをまとめて整数計画問題として定式化しましょう。
定式化:
\(\min \;\;\; \sum\limits_{i=1}^4 \sum\limits_{j=1}^4 w_{ij}x_{ij}\)
\(\;\text{s.t.}\;\;\;\sum\limits_{j=1}^4 x_{ij}=1 \;\;\;\; (i = 1,2,3,4)\)
\(\;\;\;\;\;\;\;\;\;\sum\limits_{i=1}^4 x_{ij}=1 \;\;\;\; (j = 1,2,3,4)\)
\(\;\;\;\;\;\;\;\;\; x_{ij} \in \{0,1\} \;\;(i=1,2,3,4 \; j=1,2,3,4)\)
次回の記事では今回定式化した整数計画問題をpythonで表現して実際に問題を解いてみたいと思います!
次回の記事はこちらから!
おわりに
いかがでしたか。
今回の記事では割当問題について解説していきました。
今後もこのような数理最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。