こんにちは!しゅんです!
この記事ではある会社の経営判断を数学を使って求める例を紹介したいと思います。

会社にとって、どの製品をどれくらい生産するかは非常に重要で難しい問題です。会社は自身の利益を最大化するために、どれくらいのコストをかけてどの製品をどれくらい生産するかを決定します。
ということで今回はこのような会社の問題を、数学を使って解決してみたいと思います!
それではやっていきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
今回解く問題
今回解く問題を「製品数と材料数」、「各製品の利益と生産に必要な材料の量」、「使ってよい材料の量の上限」の3つに分けて説明していきます。
製品数と材料数
今回は2種類の製品を作ることを考えます。これらは3種類の材料を使って作ることができます。
各製品の利益と生産に必要な材料の量
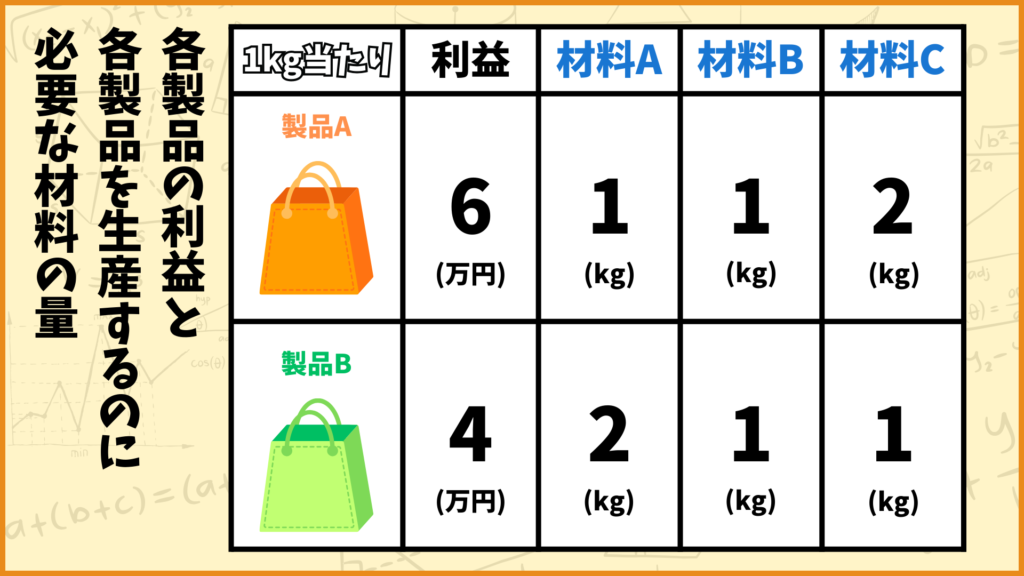
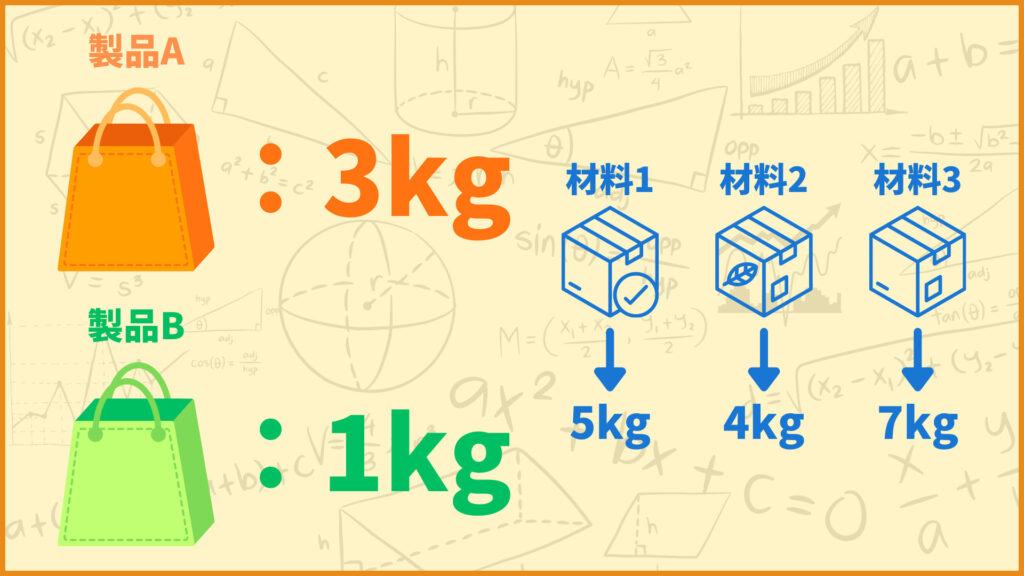
各製品を売った場合の利益と、各製品を生産するために必要な材料の量は上の表のように決まっています。この表は各製品1kg当たりの利益と、必要な材料量を表しています。
例えば製品Aの利益は1kg当たり6万円です。他にも例えば製品Bを1kg生産するためには材料Aが2kg必要となります。
今回は問題を単純にするため作った製品が全て売れるという仮定をします。
使ってよい材料の量の上限
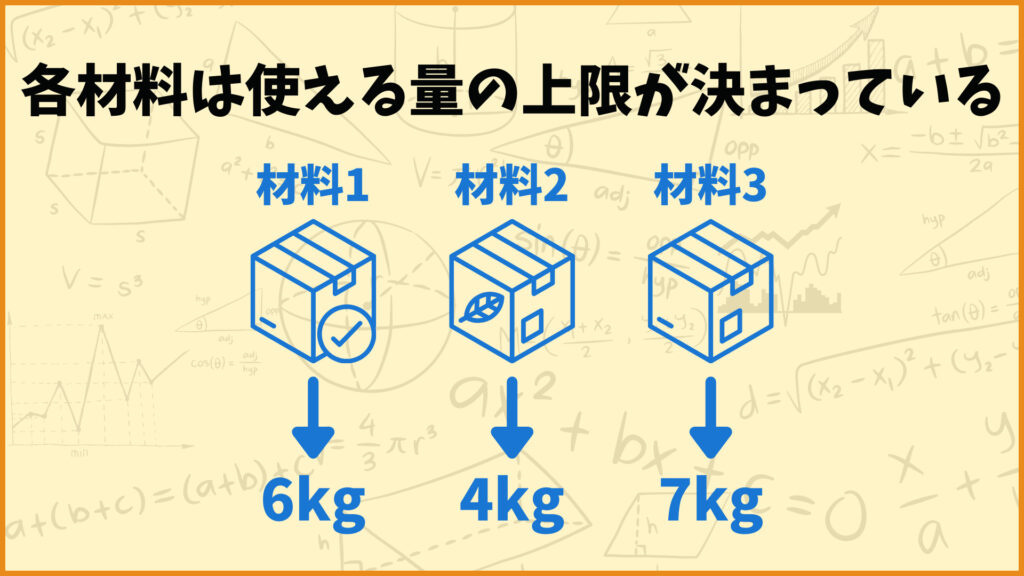
各材料にはどれくらい使っても良いかの上限が存在します。上図のように、材料1は最大で6kg、材料2は最大で4kg、材料3は最大で7kgまで使うことができます。
そのため例えば製品Aを10kg作ろうとしても、材料1,2,3の使用量の上限を超えてしまうのでそんなにたくさんは作れません。
このような制約を満たしながら会社の利益が最も大きくなるように、製品Aと製品Bをそれぞれどれくらい生産するべきかを計算していきます。
線形計画法で解く
それでは今言葉で説明したことを数式で表して実際に問題を解いていきましょう。結論から言うとこの問題は線形計画法で解くことができます。線形計画法は高校数学で登場する数学用語でしたね。
ということで線形計画法で解くために必要なことを「変数の設定」、「目的関数の設定」、「制約条件の設定」の3つに分けて説明していきます。
変数の設定

それではまず求めたいものを文字で置きましょう。今回求めたいのは
「製品Aと製品Bをどれくらい生産するか」
です。そのため今回は製品Aを\(x\)kg、製品Bを\(y\)kg生産するとしましょう。例えば\((x,y)=(3,4)\)のときは製品Aを3kg、製品Bを4kg生産することを表します。
この\(x,y\)を変数と言います。
目的関数の設定

次に今回解く問題の目的を数式で表しましょう。今回解く問題の目的は
「会社の利益を最大化する」
です。例えば製品Aを3kg、製品Bを4kg生産するときの利益を考えてみましょう。製品Aを売った時の利益は1kg当たり6万円、製品Bを売った時の利益は1kg当たり4万円です。ということで会社の利益は
\(6 \times 3 + 4 \times 4 = 34\)(万円)
となります。では製品Aを\(x\)kg、製品Bを\(y\)kg生産したときの会社の利益はどうなるでしょうか。さっきの例と同じように考えると
\(6 \times x + 4 \times y = 6x+4y\)(万円)
となりますね。これの最大値を求めれば良い訳です。ということで「会社の利益を最大化する」という日本語を「\(6x+4y\)の最大値を求める」という数式で表すことができました。
この\(6x+4y\)を目的関数と言います。
制約条件の設定

それでは最後に今回解く問題の制約を数式で表しましょう。今回の制約は
「各材料には使っても良い量の上限がある」
です。
この制約が無いと\(x,y\)をいくらでも大きくできて利益をいくらでも大きくすることができちゃいます。
例えば材料1について考えてみましょう。製品Aを1kg作るのに材料1を1kg使用し、製品Bを1kg作るのに材料1を2kg使用します。
そのため仮に製品Aを3kg、製品Bを4kg作ると、材料1の使用量は以下のように計算できます。
\(1 \times 3 + 2 \times 4 = 11\) (kg)
では製品Aを\(x\)kg、製品Bを\(y\)kg生産するとき材料1の使用量はいくらになるでしょうか。同じように考えると
\(1 \times x + 2 \times y = x + 2y\) (kg)
と表すことができます。
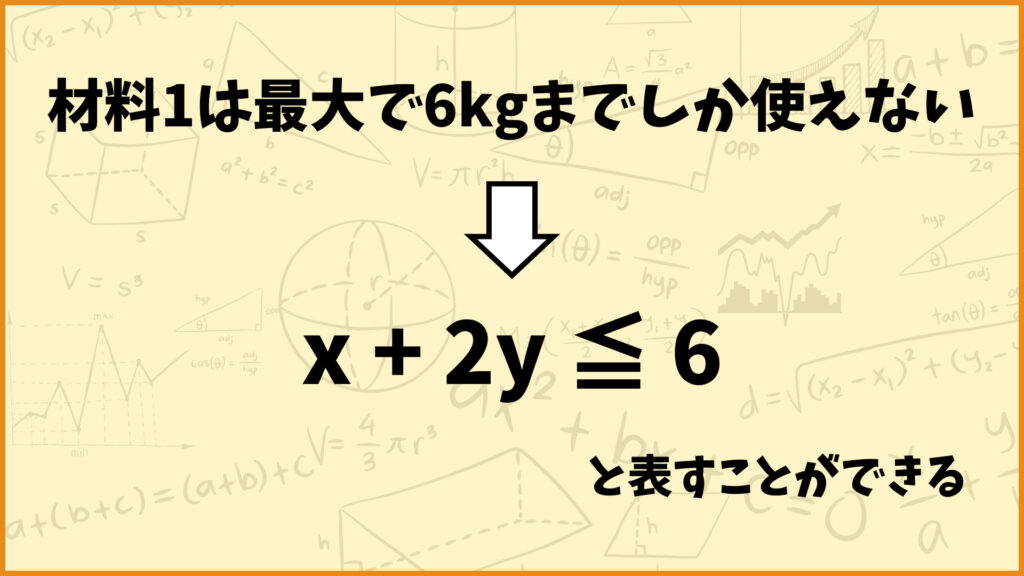
そして材料1は6kgまでしか使えません。つまり材料1の使用量\(x+2y\)を6以下に抑える必要があります。このことを数式で表すと
\(x+2y \leq 6\) (材料1に関する制約)
と表現することができます。これは材料1に関する制約ですが、他にも材料2、材料3に関する制約も存在します。これらも同じように考えると
\(x+y \leq 4\) (材料2に関する制約)
\(2x+y \leq 7\) (材料3に関する制約)
と表すことができます。
あと\(x,y\)はマイナスの値を取れないので
\(x \geq 0\)
\(y \geq 0\)
と言う制約も必要になります。ということで今回解く問題の制約を数式で表すことができました。
\(x+2y \leq 6\)
\(x+y \leq 4\)
\(2x+y \leq 7 \)
\(x \geq 0\)
\(y \geq 0\)
を制約条件と言います。
グラフを使って求める
これまで議論してきたことをまとめましょう。
製品Aを\(x\)kg、製品Bを\(y\)kg生産するとする。このとき、
\(x+2y \leq 6, \; x+y \leq 4, \; 2x+y \leq 7, \; x \geq 0, \; y \geq 0 \)
の条件のもとで
\(6x+4y\)
の最大値を求める。
上記が今回解く問題を数式で表したものです。ここまでくれば線形計画法で解けるなぁってことが分かりますね。
線形計画法をザックリ説明すると条件を満たす領域をグラフで描いて、目的関数の最適値を求める方法です。
線形計画法はこちらの記事で詳しく解説しています!
\(x+2y \leq 6, \; x+y \leq 4, \; 2x+y \leq 7, \; x \geq 0, \; y \geq 0 \)
をグラフに描くと以下のようになります。
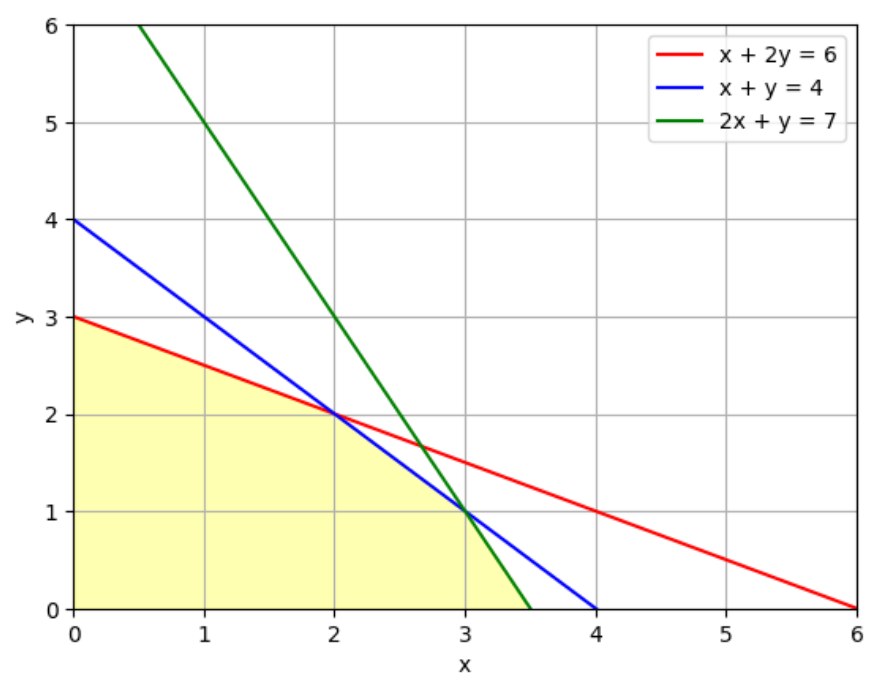
条件を満たす領域は上図の黄色の部分です。続いて\(6x+4y=k\)とおいて\(k\)を色々動かしてみましょう。
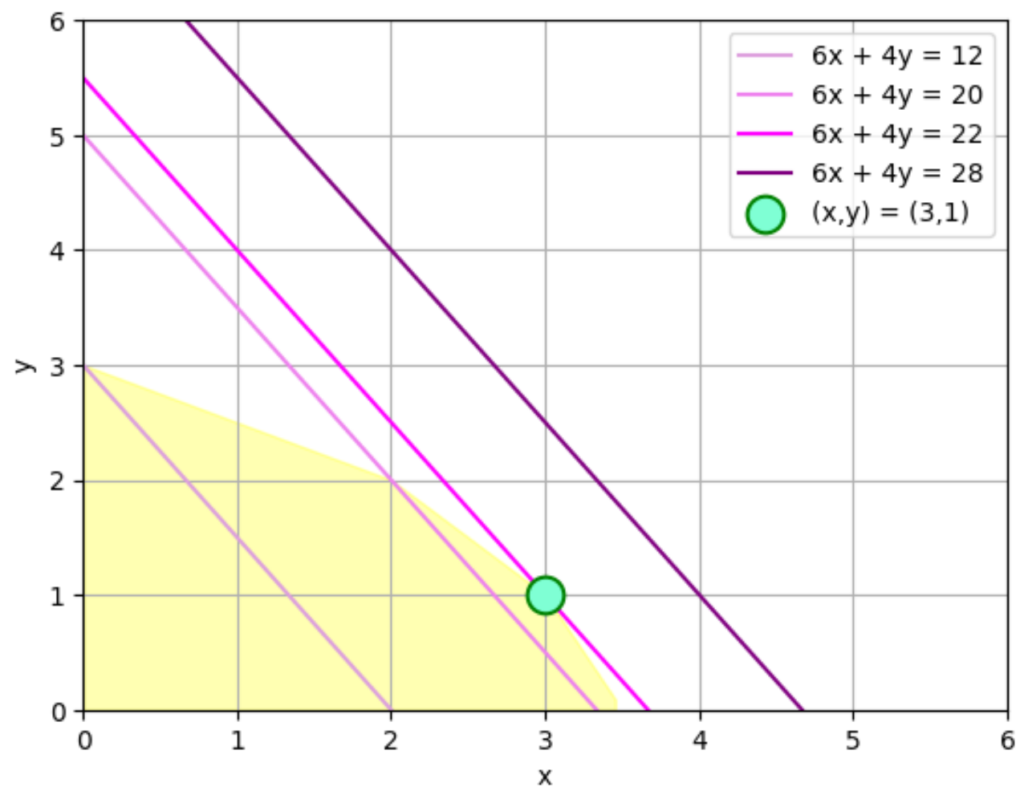
\(k=12,20,22,28\)の例を上に示しています。これを見ると\(k = 12,20\)のときは、もっと\(k\)を大きくできますが、\(k=28\)だと領域の外に出てしまいます。
そう考えると\(k = 22\)、すなわち\(6x+4y=22\)が最大値だということが分かりました。\(6x+4y=22\)のとき\((x,y) = (3,1)\)となります。
以上のことから製品Aを3kg、製品Bを1kg生産すると会社の利益を最大にすることができることが分かりました。
また各材料の使用量は材料1が5kg、材料2が4kg、材料3が7kgでちゃんと使ってよい量の範囲内になっていますね。
おわりに
いかがでしたか。
今回の記事では世の中で使われている線形計画法について解説していきました。
今後もこのような数理最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。