こんにちは!しゅんです!
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。

今回の記事ではNBAのスタッツを使ってデータ分析をしてみたいと思います!
経営工学とは少し離れるかもしれませんが、データ分析に興味がある人、NBAに興味がある人はぜひ今回の記事を読んでみてください!!!
この記事は前回からの続きなのでこれまでの記事を見てから読むと分かりやすいです!
度数分布表とヒストグラム
ヒストグラムは中学数学で習うもので、度数分布表を図に表したものです。
では度数分布表とはいったい何でしょうか?
簡単に説明すると度数分布表はデータの分布を分かりやすくまとめて表にしたものです。
例えば学校の英語のテストで考えてみましょう。
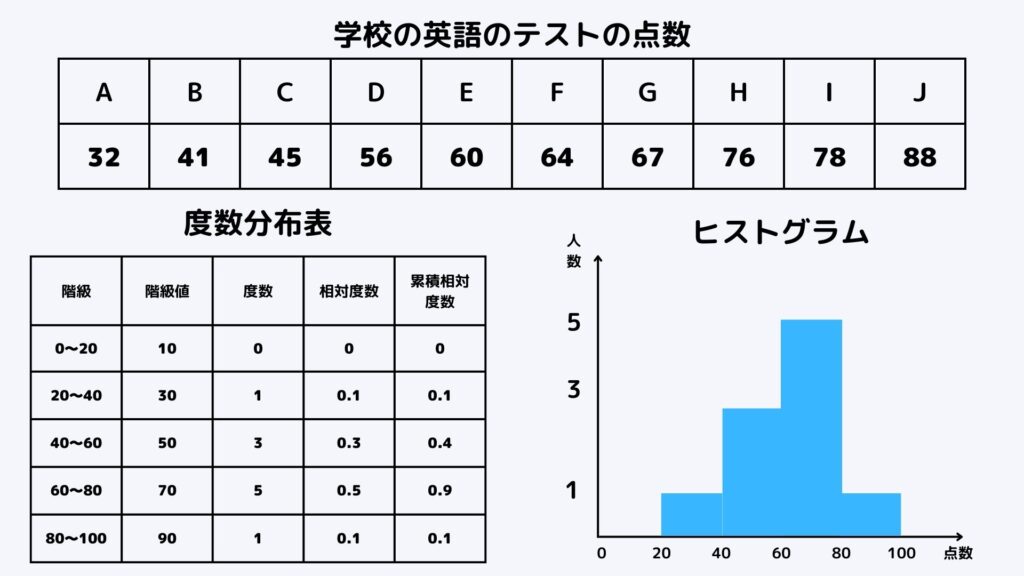
上の図の一番上の表を見てください。これは10人の英語のテストの点数を小さい順に並べたものです。
この表からまず度数分布表を作ります。1つずつ説明していきましょう。
階級
階級は点数の範囲を表しています。
今回は20点刻みでまとめてますね。0~20という行に0点から20点の情報を書き入れていきます。
度数
度数は階級に属す人数を書きます。
今回0点から20点の人がいないですね。ということで0~20の度数は0になります。
20点から40点の人は3人いるので20~40の度数は3になるというわけです。
相対度数
相対度数は全体のうちどれくらいがその階級に属しているかを表します。
計算は簡単で、度数を総人数の10で割ってください。相対度数の列を見てみると全て各度数を10で割っていることが分かります。
累積相対度数
累積相対度数はそれまでに登場した相対度数を足し算してください。
例えば40~60の累積相対度数は
(0~20の相対度数の0)+(20~40の相対度数の0.1)+(40~60の相対度数の0.4)= 0.4
という風になります。
ヒストグラムはこれらの中でも階級(点数)を横軸、度数(人数)を縦軸にしてグラフにします。
ヒストグラムがあるとデータの分布が可視化できるので非常に便利です。
ということで実際にプログラミングで度数分布表とヒストグラムを作ってみましょう!
度数分布表を作成する
それではやってみましょう。今まで使用してきたNBAのデータを今回も使っていこうと思います。
今回はpandasに加えてnumpyというモジュールも使っていこうと思います。numpyは数値計算が非常に楽に行えるので重宝しています。
# numpyをnpと認識させてインストールする
import numpy as npこれでいちいちnumpyと書かずにnpと省略できます。
度数はnp.histogram()で求めることができます。試しにFT%の度数を求めてみましょう。
# FT%のデータをnumpyの配列にする
FT_percent = np.array(df["FT%"])
# 度数を求める(今回は0から1の範囲を20個(0.05刻み)に刻む)
FT_freq = np.histogram(FT_percent, bins = 20, range = (0,1))
# 度数を表示
FT_freq[0]
とりあえず度数が求まりました。やはりFT%は右側に偏っていそうですね。
np.histogramの()の中は
(度数を求めるデータ, bins = 刻みたい数, range = (度数の範囲))
となっています。今回は%表記なので0~1の範囲を20個に刻んで0.05ずつの度数にしました。
ということで実際に度数分布表を作ってみましょう。FT%だけじゃなくて最終的には2P%や3P%のも作りたいので関数にして作ってみます。
# 関数を定義する(引数はFT%, 3P%, 2P%といったスタッツの名前)
def dosuubunpu(x):
Percent = np.array(df[x]) # データフレームをnumpyの配列にする
Dosuu = np.histogram(Percent, bins = 20, range = (0,1)) # 度数を求める(今回は0から1の範囲を20個(0.05刻み)に刻む)
Kaikyuuti = [((i + (i+5))/100)/2 for i in range(0, 100, 5)] # 階級値を求める
Soutai = Dosuu[0] / Dosuu[0].sum() # 相対度数を求める
Ruiseki = np.cumsum(Soutai) # 累積相対度数を求める
Kaikyuu =[f"{i/100}~{(i+5)/100}" for i in range(0, 100, 5)] # 階級を求める
# 度数分布表の作成
Table = pd.DataFrame({"度数":Dosuu[0]}, index=pd.Index(Kaikyuu, name = "階級"))
Table["階級値"] = Kaikyuuti # 階級値のラベルを付ける
Table["相対度数"] = Soutai # 相対度数のラベルを付ける
Table["累積相対度数"] = Ruiseki # 累積相対度数のラベルを付ける
Table =Table[["階級値","度数","相対度数","累積相対度数"]]
return Table # 度数分布表を表示# FT%の度数分布表を表示
dosuubunpu("FT%")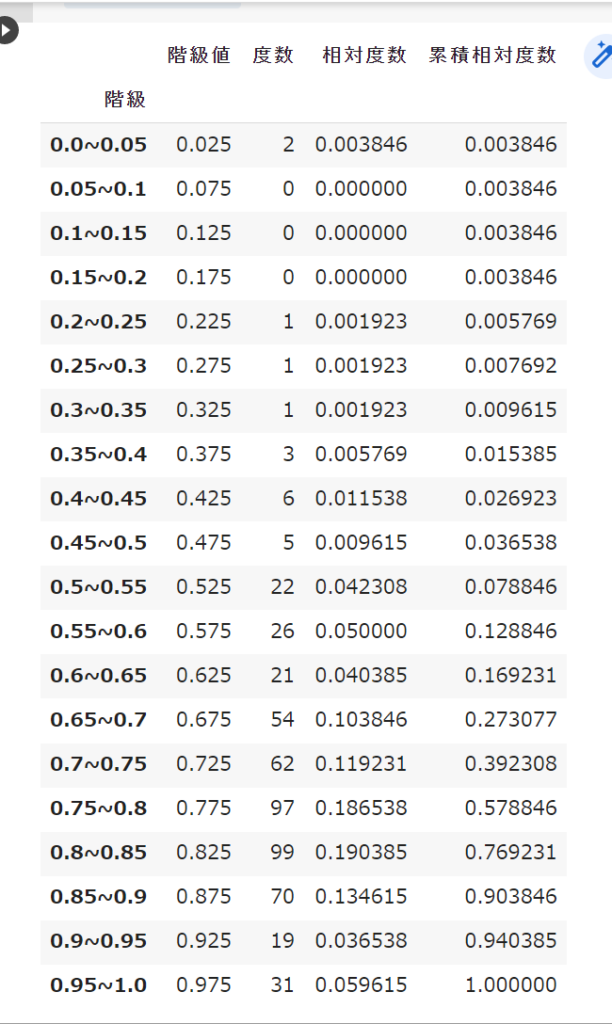
長くなりましたが度数分布表が作れました。今回は関数を定義してあとでFT%を代入しましたが、直接作ることもできます。
pythonの関数は引数を設定して何をするか定義するものです。
例えばFT%以外に3P%や2P%の度数分布表を作りたいときに毎回このコードを書くのは面倒くさいですよね。
関数にしておけば、FT%、3P%、2P%を代入するだけでできちゃいます。というわけで関数は非常に便利です。
ということで最後にヒストグラムを作ってみましょう。
ヒストグラムを作成する
今回は3P%, 2P%, FT%の3つを表示してみましょう。グラフの作成にはmatplotlibというモジュールを使っていきます。
matplotlibは様々なグラフを作成するのによく使います。
%matplotlib inline
import matplotlib.pyplot as plt
!pip install japanize-matplotlib
import japanize_matplotlib #日本語化matplotlib
import seaborn as sns
sns.set(font="IPAexGothic") #日本語フォント設定# 3P%のデータをnumpyの配列にする
Th_percent = np.array(df["3P%"])
# 2P%のデータをnumpyの配列にする
Tw_percent = np.array(df["2P%"])
# FT%のデータをnumpyの配列にする
FT_percent = np.array(df["FT%"])
# グラフ作成とグラフの大きさを宣言
fig = plt.figure(figsize=(15,12))
# 3P%のグラフを作る
ax1 = fig.add_subplot(3,1,1)
Dosuu1=ax1.hist(Th_percent,bins=20, range = (0, 1), color = "darksalmon") #ヒストグラムを作る
ax1.set_xlabel("3P%成功率") # x軸のラベルを付ける
ax1.set_ylabel("人数") # y軸のラベルを付ける
ax1.set_title("3P%成功率のヒストグラム") # タイトルをつける
ax1.set_xticks(np.linspace(0,1,20+1)) # x軸の目盛りを付ける
ax1.set_yticks(np.arange(0,200+1, 20)) # y軸の目盛りを付ける
## 以下3P%と同様
# 2P%のグラフを作る
ax2 = fig.add_subplot(3,1,2)
Dosuu2=ax2.hist(Tw_percent,bins=20, range = (0, 1), color = "lightgreen")
ax2.set_xlabel("2P%成功率")
ax2.set_ylabel("人数")
ax2.set_title("2P%成功率のヒストグラム")
ax2.set_xticks(np.linspace(0,1,20+1))
ax2.set_yticks(np.arange(0,200+1, 20))
#FT%のグラフを作る
ax3 = fig.add_subplot(3,1,3)
Dosuu3=ax3.hist(FT_percent,bins=20, range = (0, 1), color = "lightblue")
ax3.set_xlabel("FT%成功率")
ax3.set_ylabel("人数")
ax3.set_title("FT%成功率のヒストグラム")
ax3.set_xticks(np.linspace(0,1,20+1))
ax3.set_yticks(np.arange(0,200+1, 20))
plt.tight_layout() # 体裁を整える
plt.show # ヒストグラムを表示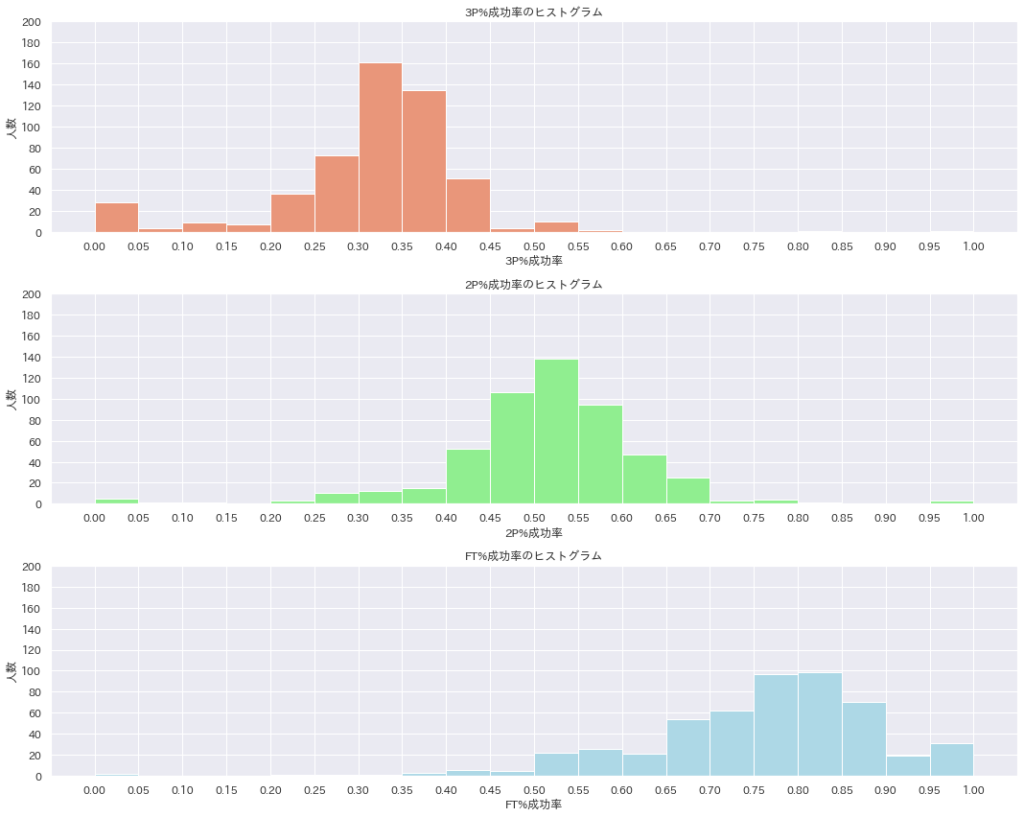
こんな感じで各スタッツのヒストグラムが完成しました。コードが長くなっていますが3P%のやつをコピペして2P%やFT%に変えちゃえばできます。
概ねぼくが予想した感じの分布になっていました。
2P%のヒストグラムがほぼ左右対称になっていてきれいですね。正規分布っぽいですね。3P%もある程度その感じがします。
FT%はどうでしょうか。思ったよりもばらけていますね。
ということでヒストグラムを見ればNBAの選手たちのシュート成功率がどのような分布になっているのかが大体わかります。
最後に全部まとめて表示してみましょうかね。
# グラフの作成とグラフの大きさの宣言
fig = plt.figure(figsize=(12,5))
ax = fig.add_subplot(1,1,1)
# 3P%, 2P%, FT%のヒストグラムを作成
Dosuu=ax.hist(Th_percent,bins=20, range = (0, 1), color = "darksalmon", alpha=0.7, label = "3P%")
Dosuu=ax.hist(Tw_percent,bins=20, range = (0, 1), color = "lightgreen",alpha=0.7, label = "2P%")
Dosuu=ax.hist(FT_percent,bins=20, range = (0, 1), color = "lightblue",alpha=0.7, label = "FT%")
# x軸、y軸の名前を設定
ax.set_xlabel("シュート成功率")
ax.set_ylabel("人数")
# タイトルを設定
ax.set_title("3P%, 2P%, FT%成功率のヒストグラム")
# x軸、y軸の目盛りを設定
ax.set_xticks(np.linspace(0,1,20+1))
ax.set_yticks(np.arange(0,200+1, 20))
plt.tight_layout() # 体裁を整える
plt.legend() # ラベルを設定
plt.show #ヒストグラムの表示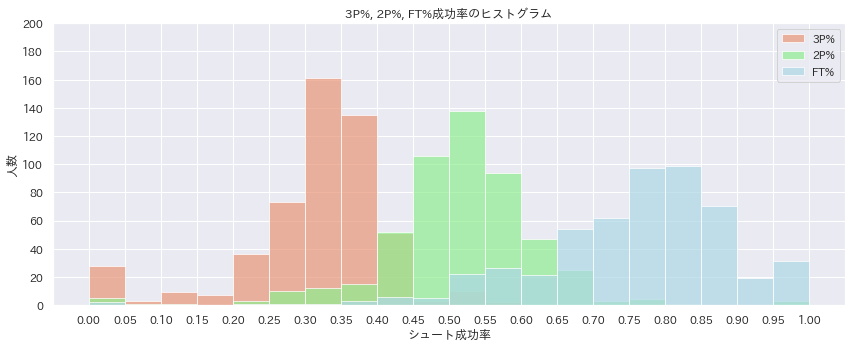
ということで完成しました。
とはいえこのヒストグラムはNBAの全選手を対象にしています。そのため前回の記事でも書きましたがシュートの試投数は考慮されていません。
それを考慮して例えば規定試投数を満たした選手の実をカウントする形にしたらヒストグラムの形はまた変わってくると思います。
いずれにせよ数字をこのようにして可視化できて非常にわかりやすくなったと思います。
今回は3P%, 2P%, FT%の3つの指標を使ってヒストグラムを作りましたが、別に成功率じゃなくて成功数にしたり、リバウンド数にしたり得点数にしたり色々とできます。
興味がある人はぜひ他のスタッツを使ってヒストグラムを作ってみてください!何か新しい発見があるかもしれません。
おわりに
いかがでしたでしょうか。
今回は度数分布表とヒストグラムについて解説していきました。これからもデータ分析について色々と話していきたいと思います。
こうやって記事を書いているとぼく自身も非常に勉強になるのでやってて非常に有意義だと思っています。
最後までこの記事を読んでくれてありがとうございました!
この記事が役に立ったら幸いです。



