こんにちは!しゅんです!
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。

今回の記事ではNBAのスタッツを使ってデータ分析をしてみたいと思います!
経営工学とは少し離れるかもしれませんが、データ分析に興味がある人、NBAに興味がある人はぜひ今回の記事を読んでみてください!!!
この記事は前回からの続きなので前回までの記事を見ると分かりやすいです!
散布図ってなに?
それではまず散布図の説明からしていきましょう。
例として今AさんからFさんの6人が英語と数学のテストを受けたと仮定しましょう。
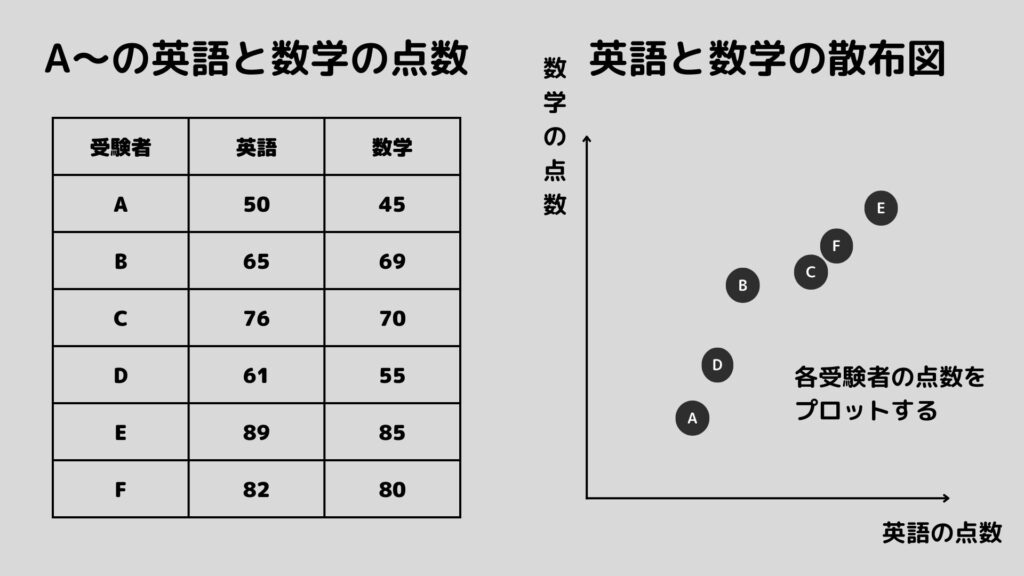
ということでテストが上図のような結果だったとしましょう。
今回は横軸を英語の点数、縦軸を数学の点数にして散布図を作ってみました。これは各受験者ごとに(英語の点数、数学の点数)の座標のところに点をプロットしていったものです。
散布図を作ることによって2つのデータがどのような関係になっているかが分かります。
例えば上の散布図を見ると右肩上がりになっていますね。
これはつまり英語の点数が高いと数学の点数が高く、英語の点数が低いと数学の点数が低い傾向があることを表しています。
このように右肩上がりの図になる場合は正の相関があると言います。逆に右肩下がりの図になる場合は負の相関があると言います。
どちらも高校数学で学ぶ概念なので気になる人は勉強してみると面白いと思います。
少し話がそれてしまいますが相関関係と因果関係の話は聞いたことあるでしょうか。
少し難しい話ですが、相関関係があるからといって因果関係があるとは限らないといった趣旨の話です。
因果関係とは2つの事柄の間に原因と結果の関係あるかどうかということです。
上の図でいえば英語の点数が高いと数学の点数も高いということは言えるけど(相関関係がある)英語の点数が高かったから数学の点数も高かったとは限らない(因果関係がある)ということです。
この違いはかなり重要なので知っておくべきだと思います。ネットで調べたら色々出てくるので「相関関係 因果関係」などと調べてみると面白いと思います!
今回は本題ではないので飛ばします。
ということで実際にNBAのデータを使って散布図を作っていきましょう!
散布図を作ってみる
今回も前回と同様google colabを使ってプログラミングしていきたいと思います。
また前回と同様にNBAのデータはdfとして読み込み済みです。詳しいことはPart 1のデータの前処理のところで話しています!
散布図を作るためには2種類のデータが必要になります。
# 散布図の大きさを設定
fig = plt.figure(figsize = [20,6])
# 3P%と2P%の散布図を作成
ax1 = fig.add_subplot(131)
ax1.scatter(df["3P%"], df["2P%"], color = "darksalmon") # 3P%と2P%の散布図を作成
plt.xlabel("3P%") # x軸のラベルを付ける
plt.ylabel("2P%") # y軸のラベルを付ける
# 3P%とFT%の散布図を作成
ax2 = fig.add_subplot(132)
ax2.scatter(df["3P%"], df["FT%"], color = "cyan") # 3P%と2P%の散布図を作成
plt.xlabel("3P%") # x軸のラベルを付ける
plt.ylabel("FT%") # y軸のラベルを付ける
# 2P%とFT%の散布図を作成
ax3 = fig.add_subplot(133)
ax3.scatter(df["2P%"], df["FT%"], color = "lightgreen") # 3P%と2P%の散布図を作成
plt.xlabel("2%") # x軸のラベルを付ける
plt.ylabel("FT%") # y軸のラベルを付ける
# 散布図を表示
plt.show()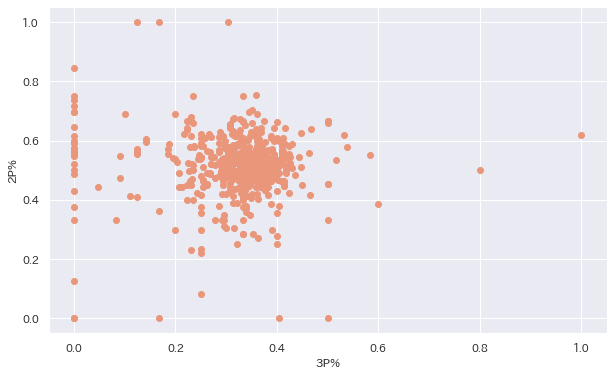
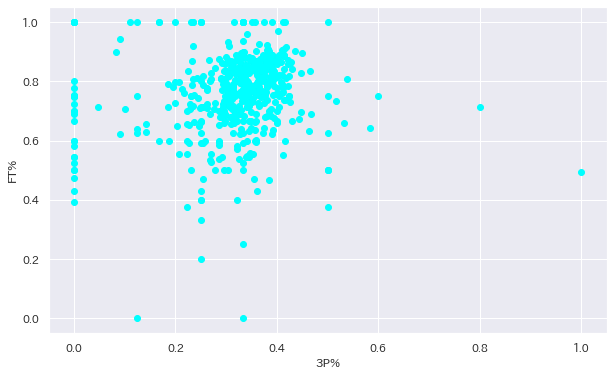
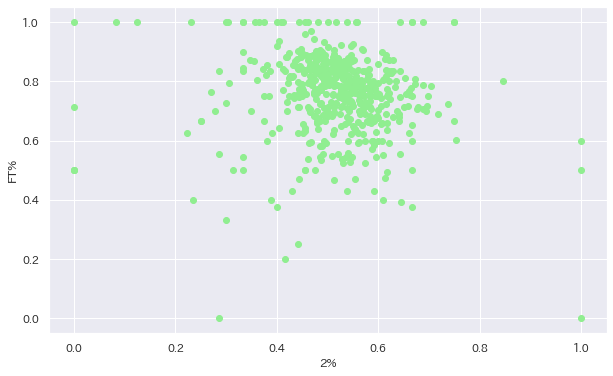
ということでとりあえず何も考えずに散布図を作ってみました、どうでしょうか。この図を見ると特にシュート率に関して相関はなさそうに見えますね。
実際はどうなんでしょうか。以前どこかで「NBAで3Pが入らない選手は大体FT成功率が低い」という話を聞いたことがあります。
ということで今度はFT%と3P%に絞って考えていこうと思います。
3P%とFT%の関係を考える
先ほどの3P%とFT%の散布図を見てみるとあまり関係がないように思えます。
ではぼくが聞いた「NBAで3Pが入らない選手はFT%も低い」という説は間違いなのでしょうか。
ということで色々条件を付けてみましょう。
3P試投数とFT試投数に制限を付ける
散布図を見るとそれぞれ0や1に張り付いている点がありますよね。
なぜこのようなことが起こっているのでしょうか。
これはおそらく試投数が関係していると考えられます。例えば3Pをほぼ打たないCの選手は3P%が0や1になっている可能性があります。
ということでこれらを排除する条件を付けてみましょう。
df_0 = df[df["3PA"] >= df["3PA"].mean()] # 3PAが平均以上のデータだけ抽出(3PAは3P試投数)
df_0 = df_0[df_0["FTA"] >= df["FTA"].mean()] # FTAが平均以上のデータだけ抽出(FtAはFT試投数)
# 散布図の大きさを設定
fig = plt.figure(figsize = [10,6])
# 3P%とFT%の散布図を作成
ax = fig.add_subplot(111)
ax.scatter(df_0["3P%"], df_0["FT%"], color = "cyan") # 3P%と2P%の散布図を作成
plt.xlabel("3P%") # x軸のラベルを付ける
plt.ylabel("FT%") # y軸のラベルを付ける
# 散布図を表示
plt.show()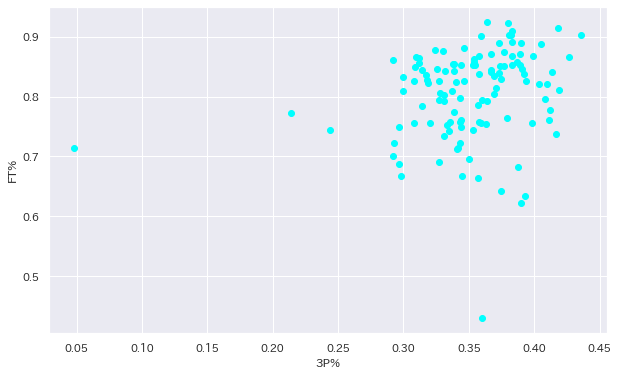
ということでできました。さっきよりもすっきりして幾分か見やすくなっています。
どうでしょうか。個人的には若干ですが正の相関があるように感じます。
ここから相関係数を求めたり回帰直線を求めたりすることもできますが、今回は散布図を書くことが目的なので気が向いたらまた別の記事でやってみようと思います。
散布図を見ると2点ほど外れ値がありますね。誰のデータか見てみましょう。
# 3P%が0.05未満のデータを抽出
df_0[df_0["3P%"] < 0.05]
# FT%が0.5未満のデータを抽出
df_0[df_0["FT%"] < 0.5]
どうやらこの2人の選手らしいです。G(出場試合数)を見るとどちらも1桁なのでほとんど試合に出てないですね。
でもMP(出場試合分数)を見ると出た試合では2人ともかなりの分数出場していますね。何かあったんでしょうか。
どちらもサンダーの選手ですね。
PTSも出た試合ではまずまずな結果です。怪我とかでしょうか?
ちょっと気になってきたので今度調べてみようかな笑
話しが脱線しましたが、このように散布図を見て外れ値などが確認できます。例えばここからさらに分析をする場合にはこれらを除外して考える必要があります。
それでは次にポジションごとで分けてみましょう。
ポジションごとに分けて考えてみる
ということでポジションごとに色分けして散布図を表示してみます。
df_0 = df[df["3PA"] >= df["3PA"].mean()] # 3PAが平均以上のデータだけ抽出(3PAは3P試投数)
df_0 = df_0[df_0["FTA"] >= df["FTA"].mean()] # FTAが平均以上のデータだけ抽出(FTAはFT試投数)
# 散布図の大きさを設定
fig = plt.figure(figsize = [10,6])
# 3P%とFT%の散布図を作成
ax = fig.add_subplot(111)
ax.scatter(df_0[df_0["Pos"] == "PG"]["3P%"], df_0[df_0["Pos"] == "PG"]["FT%"], color = "red", alpha = 0.5, label = "PG") # 3P%と2P%の散布図を作成
ax.scatter(df_0[df_0["Pos"] == "SG"]["3P%"], df_0[df_0["Pos"] == "SG"]["FT%"], color = "blue", alpha = 0.5, label = "SG") # 3P%と2P%の散布図を作成
ax.scatter(df_0[df_0["Pos"] == "SF"]["3P%"], df_0[df_0["Pos"] == "SF"]["FT%"], color = "green", alpha = 0.5, label = "SF") # 3P%と2P%の散布図を作成
ax.scatter(df_0[df_0["Pos"] == "PF"]["3P%"], df_0[df_0["Pos"] == "PF"]["FT%"], color = "purple", alpha = 0.5, label = "PF") # 3P%と2P%の散布図を作成
ax.scatter(df_0[df_0["Pos"] == "C"]["3P%"], df_0[df_0["Pos"] == "C"]["FT%"], color = "salmon", alpha = 0.5, label = "C") # 3P%と2P%の散布図を作成
plt.xlabel("3P%") # x軸のラベルを付ける
plt.ylabel("FT%") # y軸のラベルを付ける
ax.legend()
# 散布図を表示
plt.show()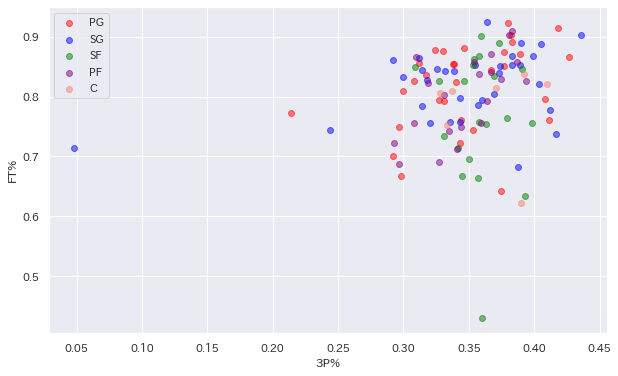
とりあえず色分けしてみましたがとても分かりずらいです。ということでポジションごとに散布図を分けて5つの散布図を表示してみましょう。
df_0 = df[df["3PA"] >= df["3PA"].mean()] # 3PAが平均以上のデータだけ抽出(3PAは3P試投数)
df_0 = df_0[df_0["FTA"] >= df["FTA"].mean()] # FTAが平均以上のデータだけ抽出(FTAはFT試投数)
# 散布図の大きさを設定
fig = plt.figure(figsize = [15,15])
# PGの散布図を作成
ax1 = fig.add_subplot(321)
ax1.scatter(df_0[df_0["Pos"] == "PG"]["3P%"], df_0[df_0["Pos"] == "PG"]["FT%"], color = "red") # 3P%と2P%の散布図を作成
plt.xlabel("3P%") # x軸のラベルを付ける
plt.ylabel("FT%") # y軸のラベルを付ける
ax1.set_xlim(0, 0.5) # x軸の描画範囲を設定する
ax1.set_ylim(0.4,1.0) # y軸の描画範囲を設定する
ax1.set_title("PG")
# SGの散布図を作成
ax2 = fig.add_subplot(322)
ax2.scatter(df_0[df_0["Pos"] == "SG"]["3P%"], df_0[df_0["Pos"] == "SG"]["FT%"], color = "blue") # 3P%と2P%の散布図を作成
plt.xlabel("3P%") # x軸のラベルを付ける
plt.ylabel("FT%") # y軸のラベルを付ける
ax2.set_xlim(0, 0.5) # x軸の描画範囲を設定する
ax2.set_ylim(0.4,1.0) # y軸の描画範囲を設定する
ax2.set_title("SG")
# SFの散布図を作成
ax3 = fig.add_subplot(323)
ax3.scatter(df_0[df_0["Pos"] == "SF"]["3P%"], df_0[df_0["Pos"] == "SF"]["FT%"], color = "green") # 3P%と2P%の散布図を作成
plt.xlabel("3P%") # x軸のラベルを付ける
plt.ylabel("FT%") # y軸のラベルを付ける
ax3.set_xlim(0, 0.5) # x軸の描画範囲を設定する
ax3.set_ylim(0.4,1.0) # y軸の描画範囲を設定する
ax3.set_title("SF")
# PFの散布図を作成
ax4 = fig.add_subplot(324)
ax4.scatter(df_0[df_0["Pos"] == "PF"]["3P%"], df_0[df_0["Pos"] == "PF"]["FT%"], color = "purple") # 3P%と2P%の散布図を作成
plt.xlabel("3P%") # x軸のラベルを付ける
plt.ylabel("FT%") # y軸のラベルを付ける
ax4.set_xlim(0.05, 0.45) # x軸の描画範囲を設定する
ax4.set_ylim(0.4,1.0) # y軸の描画範囲を設定する
ax4.set_title("PF")
# Cの散布図を作成
ax5 = fig.add_subplot(325)
ax5.scatter(df_0[df_0["Pos"] == "C"]["3P%"], df_0[df_0["Pos"] == "C"]["FT%"], color = "salmon") # 3P%と2P%の散布図を作成
plt.xlabel("3P%") # x軸のラベルを付ける
plt.ylabel("FT%") # y軸のラベルを付ける
ax5.set_xlim(0.05, 0.45) # x軸の描画範囲を設定する
ax5.set_ylim(0.4,1.0) # y軸の描画範囲を設定する
ax5.set_title("C")
plt.tight_layout() # 体裁を整える
# 散布図を表示
plt.show()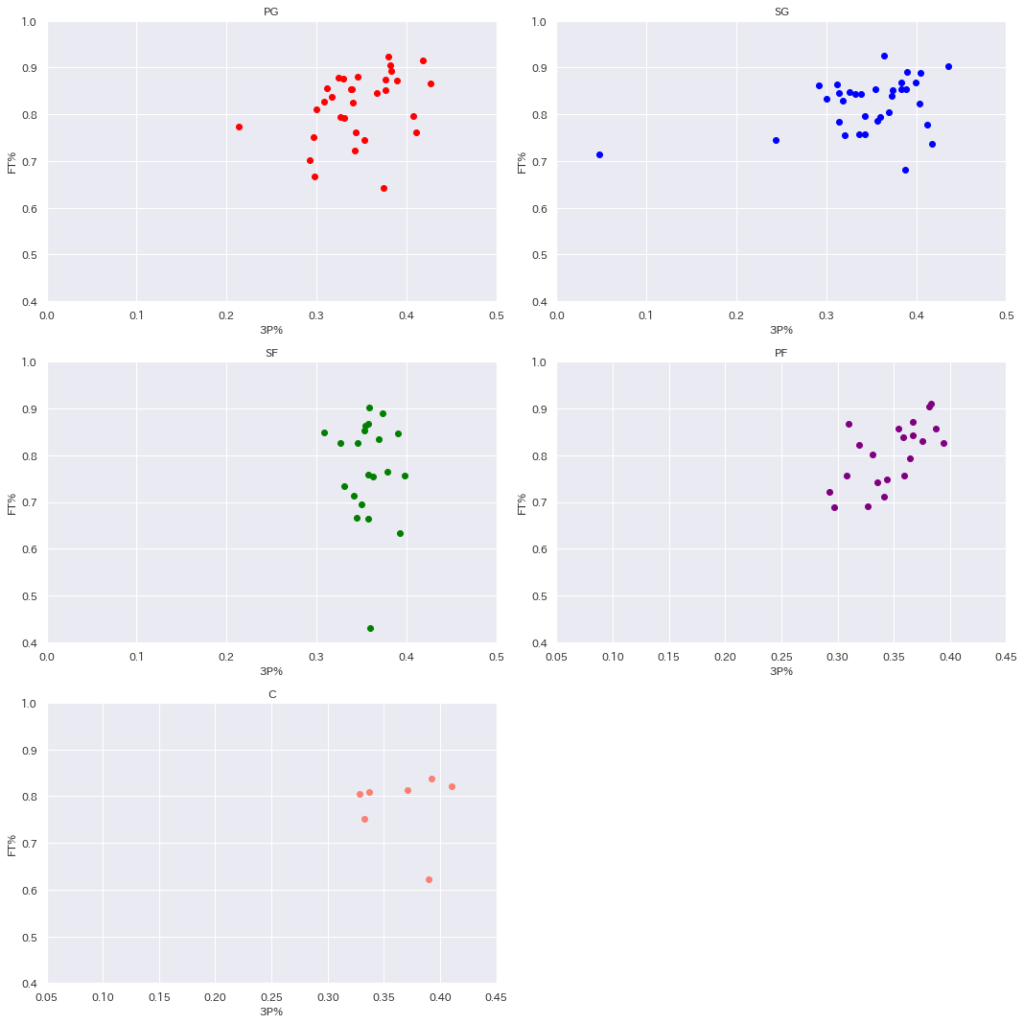
コードがかなり長くなっていますが、PGの散布図をコピペして”PG”のところを各ポジション名に変更しているだけです。
かなり分かりやすくなりました。
これを見るとPFが一番わかりやすいですね。PFに関しては3P%とFT%には正の相関があると言えそうです。
PG, SGも若干の正の相関があるように思えます。SFはどうでしょうか?
SFには相関はないですね。FTの成功率が高かろうが低かろうが3Pにはほぼ影響されていないように見えます。
Cはそもそも点の数が少なくてあまり参考になりませんね。これは3PAの数値が平均以上のデータのみ取ってきているからだと考えられます。
Cは一般的に他のポジションに比べて3Pを打たないのでそもそもリーグ平均以上の3Pを打っている選手がほとんどいないのだと思います。
条件を全選手平均以上からCの選手平均以上にしたらもう少し情報が得られると思うので皆さんもやってみてください!
ここまで色々と散布図を見て分析してみましたが、やはり3Pの上手さとFTの上手さはある程度の相関はあるのではないかと考えられます。
そしてその相関はポジションによってかなり変化し、PFが最も相関がありSFが最も相関がないことも今回の分析で分かりました。
おわりに
いかがでしたでしょうか。
今回は散布図を使って特に3P%とFT%の関係について調べていきました。
同じようにすれば2P%とFT%や3P%とPTS(平均得点数)など、様々なデータの関係を探ることができます。
違うデータを使えばきっと何か新しい発見ができると思います!
最後までこの記事を読んでくれてありがとうございました。
この記事が役に立ったら幸いです。



