【DEAってなにやってるの？】データ包絡分析法（DEA）に登場する数式の意味とpythonで実装する方法を解説してみた

こんにちは！しゅんです！

この記事ではデータ包絡分析法（DEA）について解説したいと思います！

ぼくが初めてDEAを勉強したときは、数式が難しくてよく分からなかった記憶があります。

こんな感じで非常に悩んでいました。ということでこの記事ではDEAの数式の意味、そしてDEAをpythonで実装する方法を解説して、これらの疑問を解決していきたいと思います！

それではやっていきましょう！

DEAを超ざっくり説明するとどれくらい効率的かを分析する手法です。

・店舗A～店舗Eの中で効率的に経営できている店舗はどこか
・バスケの選手Aは効率的にプレイできているか
・20時間のテスト勉強で85点取れたのは効率的なのか

などなど、お店や人がどれくらい効率的に活動できたかを分析することができます…と言われてもよく分からないので具体例を使って紹介したいと思います。

効率よく経営してるお店はどれ？（1入力1出力の例）

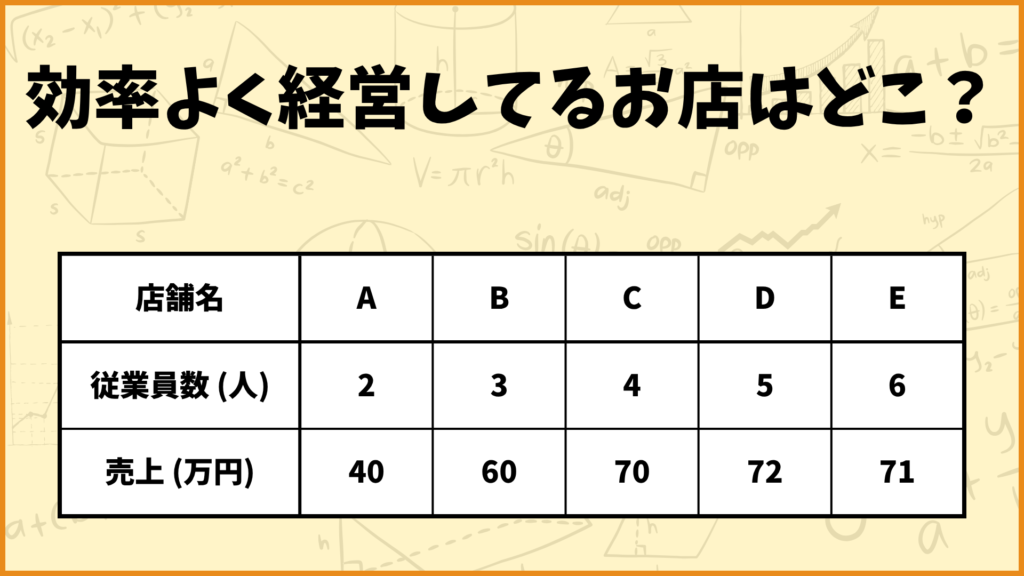
ある会社は5つの店舗A～Eを持っています。それぞれのお店の従業員数と売上は上の表のようになっています。では、この5つの店舗はどれくらい効率的に経営できているでしょうか。

パって思いつくのは「従業員1人当たりどれくらい売り上げているか計算すれば良いんじゃないか？」だと思います。すなわち各店舗に対して下記の計算を行います。

\(\text{1人当たりの売上} = \frac{\text{売上}}{\text{従業員数}}\)

ということで各店舗に対して1人当たりの売上を計算してみましょう。

店舗A：\(\frac{40}{2} = 20[\text{万円}]\)
店舗B：\(\frac{60}{3} = 20[\text{万円}]\)
店舗C：\(\frac{70}{4} = 17.5[\text{万円}]\)
店舗D：\(\frac{72}{5} = 14.4[\text{万円}]\)
店舗E：\(\frac{71}{6} = 11.83[\text{万円}]\)

これを見ると店舗Aと店舗Bが最も効率よく経営できていることが分かります。このようにDEAでは効率的であることを「少ない入力（従業員数）で多くの出力（売上）を作る」と考えます。

より一般に効率値は以下の計算式で計算できます。

\(\text{効率値} = \frac{\text{出力値}}{\text{入力値}}\)

今度はこれをグラフを使って考えてみます。

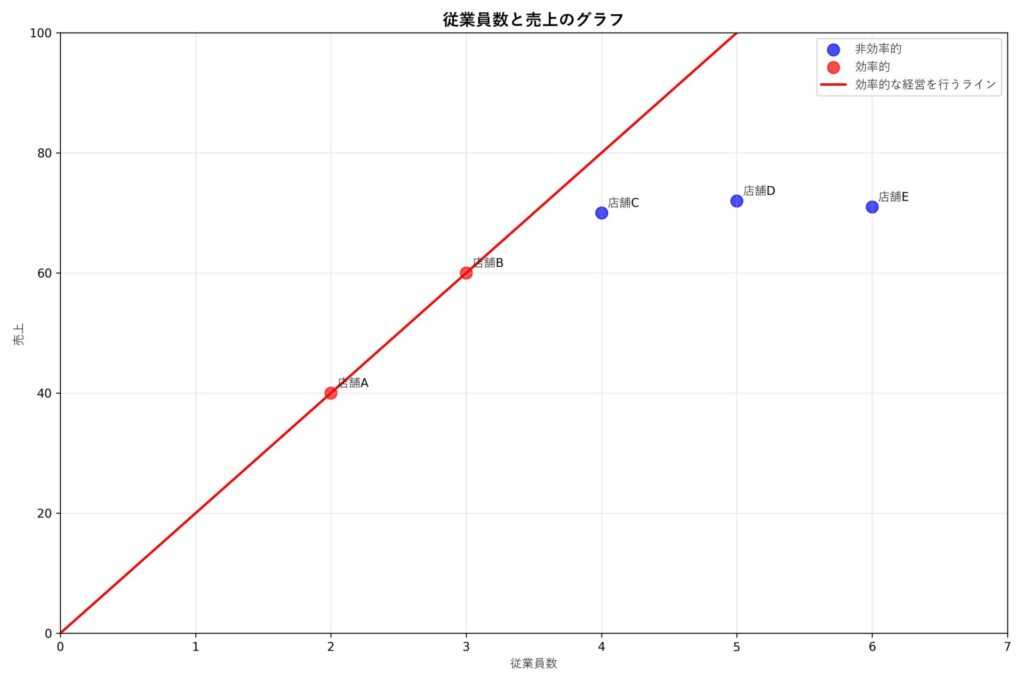
先ほど1人当たりの売上を計算しましたが、これは原点と各店舗を表す点を結んだ直線の傾きを表しています。

例えば店舗A,Bは1人当たりの売上が20万円でしたが、これは赤い直線の傾きを表しています。つまり傾きが急なほど効率的な経営ができているということです。

店舗C,D,Eはこの直線よりも下側に位置しているので、効率的ではないっていう風に捉えることができますね。こんな感じでグラフを使うと理解しやすいかもしれません。

次に店舗Cに着目して、どうすれば効率的な経営ができるかを考えていきます。

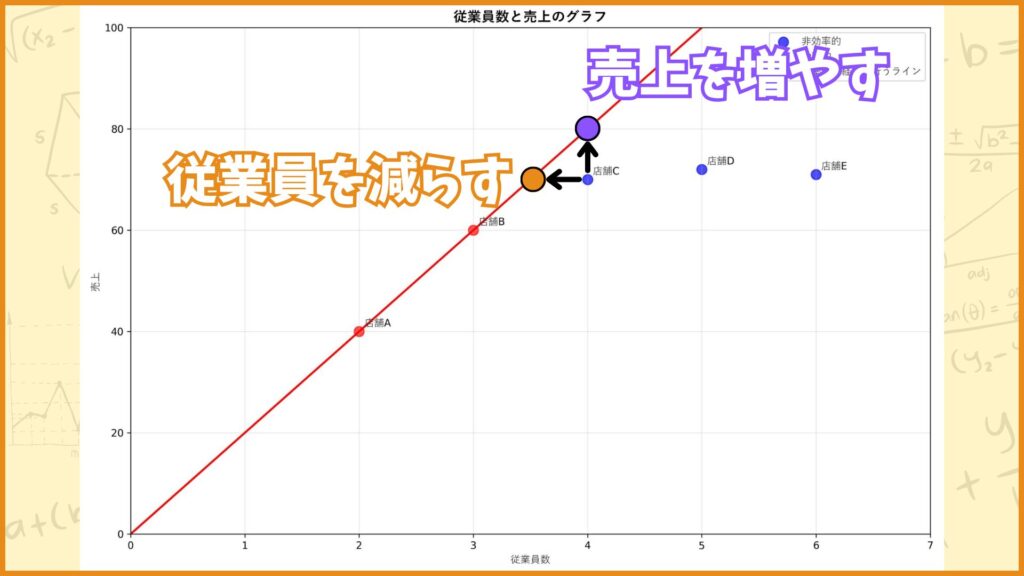
今店舗Cは赤い直線の下側に位置しているので、効率的な経営はできていません。効率的な経営を行うためには2つの方法があります。

1つ目の方法：従業員を減らす
2つ目の方法：売上を減らす

1つ目の方法について考えてみましょう。今店舗Cの従業員数は4人ですが、売上を減らさずに赤い直線上に乗るためには従業員数を3.5人まで減らす必要があります。

2つ目の方法について考えてみましょう。今店舗Cの売上は70万円ですが、従業員を減らさずに赤い直線上に乗るためには売上を80万円まで増やす必要があります。

生産性が高い機械はどれ？（2入力1出力の例）

ここまで入出力がそれぞれ1つずつの例を考えていましたが、DEAでは入出力の項目が複数あっても適用することができます。

ここでは2入力1出力の例を見ていきます。

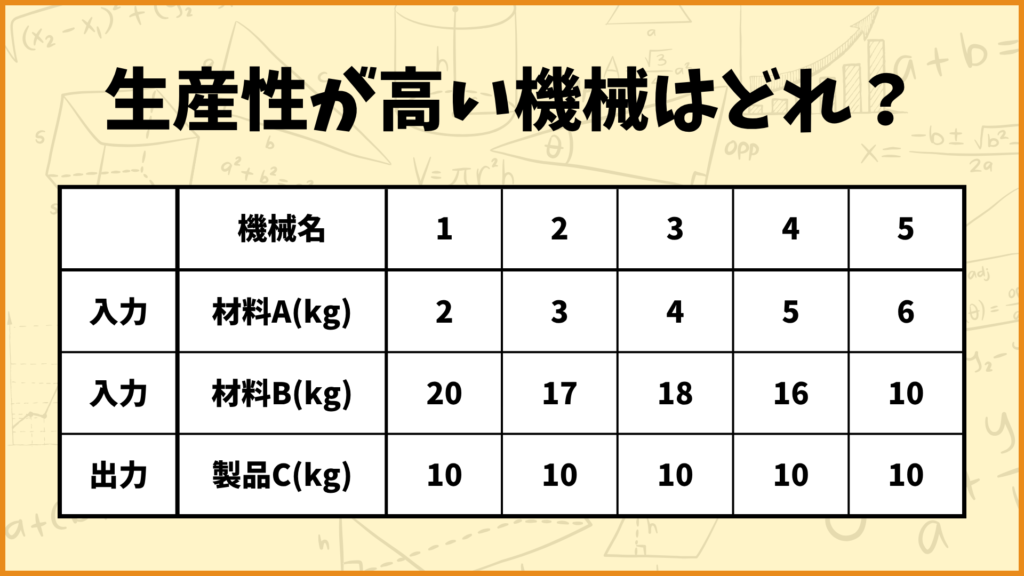
別の問題を考えてみましょう。5つの機械の生産性について考えます。どの機械も材料A、材料Bを投入して、製品Cを生産します。

また製品Cを10kg生産するのに必要となる材料A,Bの量が上の表にまとめられています。（例えば機械1は製品Cを10kg生産するために材料Aを2kg、材料Bを1kg必要とします。）

そして材料A,材料B,製品Cの価格は下記のようになっています。

このとき最も生産性が高い機械はどれでしょうか。これもさっきと同じように下記の式を使って計算します。

\(\text{効率値} = \frac{\text{出力値}}{\text{入力値}}\)

ですがこの問題例では入力値が2つあり、また価格の情報が与えられていますね。そのため今回は下記のように効率値を計算することができます。

\(\text{効率値} = \frac{(\text{製品Cの価格})\times(\text{製品Cの生産量})}{(\text{材料Aの価格})\times(\text{材料Aの投入量}) + (\text{材料Bの価格})\times(\text{材料Bの投入量})}\)

分母が材料費の総額で、分子が売上の総額みたいな感じです。

上の式に従って各機械の効率値を計算してみましょう。

\(\text{機械1の効率値} = \frac{30 \times 10}{100 \times 2 + 5 \times 20} = \frac{300}{300}=1.0\)
\(\text{機械2の効率値} = \frac{30 \times 10}{100 \times 3 + 5 \times 17} = \frac{300}{385}=0.78\)
\(\text{機械3の効率値} = \frac{30 \times 10}{100 \times 4 + 5 \times 18} = \frac{300}{490}=0.61\)
\(\text{機械4の効率値} = \frac{30 \times 10}{100 \times 5 + 5 \times 16} = \frac{300}{580}=0.52\)
\(\text{機械5の効率値} = \frac{30 \times 10}{100 \times 6 + 5 \times 10} = \frac{300}{650}=0.46\)

これを見ると機械1の効率が最も良いということが分かります。では今度は材料A,材料B,製品Cの価格が下記のようになっていたらどうでしょうか。

各機械の効率値を計算してみましょう。

\(\text{機械1の効率値} = \frac{30 \times 10}{10 \times 2 + 24 \times 20} = \frac{300}{500}=0.60\)
\(\text{機械2の効率値} = \frac{30 \times 10}{10 \times 3 + 24 \times 17} = \frac{300}{438}=0.68\)
\(\text{機械3の効率値} = \frac{30 \times 10}{10 \times 4 + 24 \times 18} = \frac{300}{472}=0.64\)
\(\text{機械4の効率値} = \frac{30 \times 10}{10 \times 5 + 24 \times 16} = \frac{300}{434}=0.69\)
\(\text{機械5の効率値} = \frac{30 \times 10}{10 \times 6 + 24 \times 10} = \frac{300}{300}=1.0\)

今度は機械5の効率値が最も良くなりましたね。

このように入力と出力が同じ値でも、係数が異なればどの機械が効率的になるのかが変わります。DEAでは各DMUに対して最も効率値が大きくなるような係数を求めます。

なんですが、ここで一つ注意しないといけないのは、係数に何の制約もつけないと効率値が無限に大きくなってしまうことです。

極端な話、材料A:1万円、材料B:1万円、製品C:1000万円にするとどの機械の効率値もめっちゃ大きくなるのが簡単に想像できます。

これを解消するためにDEAでは「どのDMUも効率値が1以下になる」という制約を考えます。

左の係数はどの機械も効率値が1以下になるのでOKな例です。一方で右の係数は機械5の効率値が1.33…となり1を超えるので、NGな例となっています。

グラフを使って考えてみる（2入力1出力の例）

次にグラフを使って考えてみましょう。

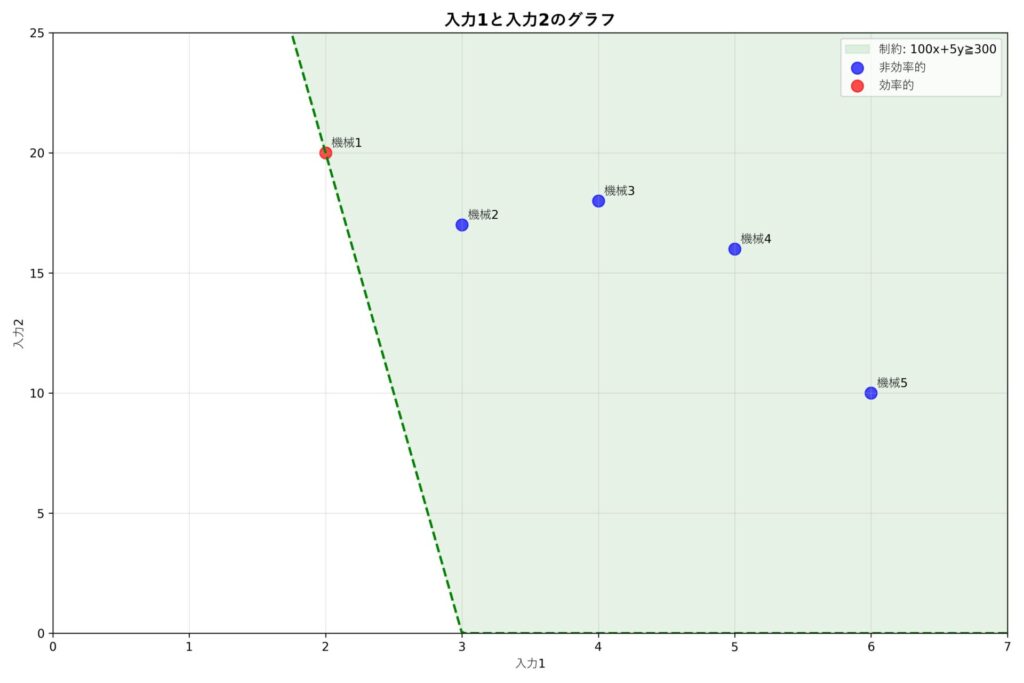
上のグラフは横軸が入力1、縦軸が入力2のグラフです。緑色の点線はパターン1の係数を表しています。すなわち \(100x+5y=300\) のラインで、このライン上にいる機械（機械1）は効率値が1になります。

また薄緑のエリアは \(100x+5y\leq 300\) を表しています。このエリアにいる機械は効率値が1以下になります。

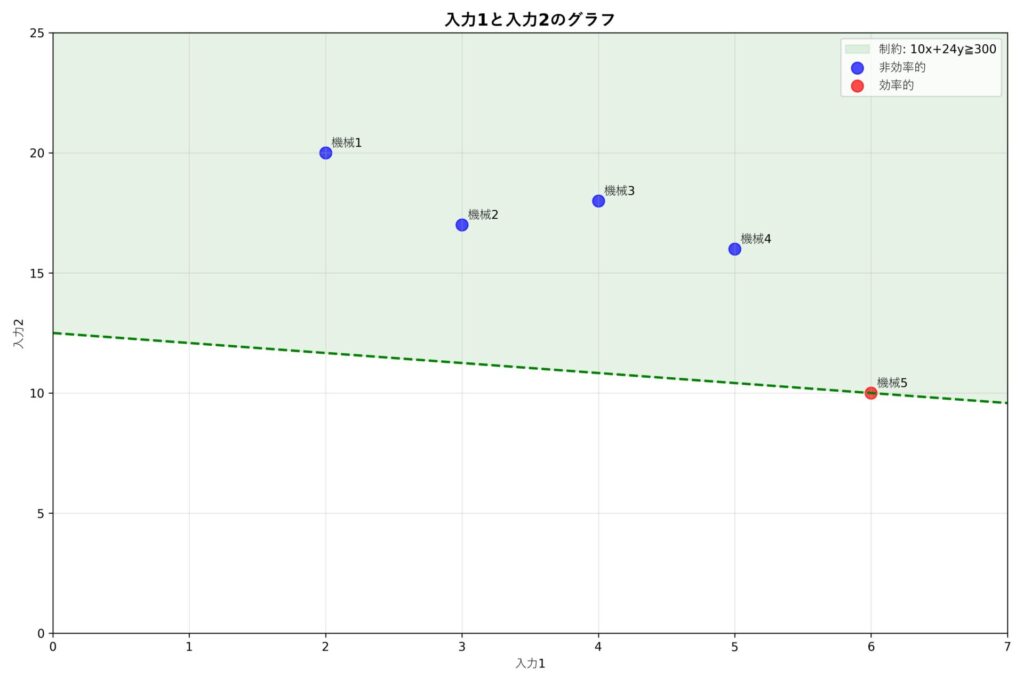
緑色の点線はパターン2の係数を表しています。すなわち \(10x+24y=300\) のラインで、このライン上にいる機械（機械5）は効率値が1になります。

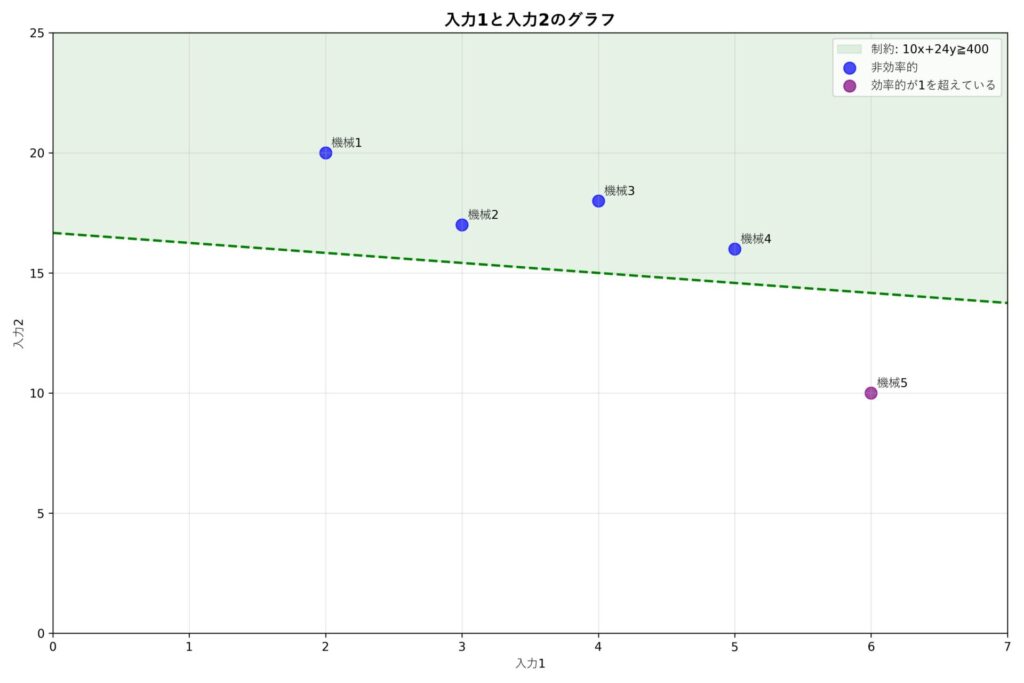
上図は先ほど紹介したNGな係数の例をグラフにしたものです。機械5を見ると緑の範囲\((10x+24y\leq400)\)の外側に位置していますね。DEAでは全ての点がこの緑の範囲に入ってないといけないので、このような係数例は除外する必要があります。

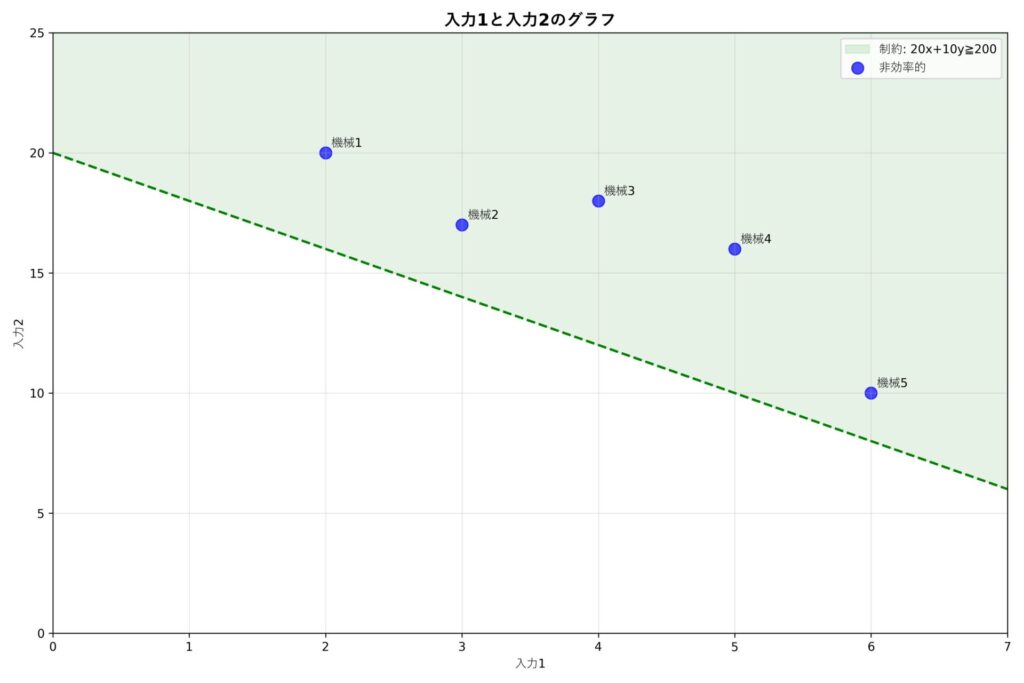
上の係数例はどの機械も効率的ではない、すなわち全てのDMUの効率値が1未満となる例です。

ここまで色々な係数例を使って効率値を考えてみましたが、

「どう頑張っても機械3と機械4は効率的にならないじゃん！」

と思いませんでしたか？そうなんです。実はどんな係数を選んでも全ての機械の効率値が1以下となり、かつ機械3,4の効率値が1にはならないんです。先ほど「DEAでは各DMUに対して効率値が最も大きくなる係数を選ぶ」と説明しましたが、機械3,4のようにどう頑張っても効率値が1未満になる場合も存在することに注意してください。

文字を使って考えてみる（2入力1出力の例）

ここまでは具体的な数値を使って説明しましたが、より一般に文字を使って話したいと思います。

上の式は2入力1出力の場合を書いています。DEAでは各DMUに対して効率値\(\frac{u_1y_{1j}}{v_1x_{1j}+v_2x_{2j}}\)が最も大きくなるように係数\(u_1,v_1,v_2\)の値を決めます。

ただこのままだと効率値が無限に大きくなってしまうので、全てのDMUの効率値が1以下になるという制約を付けるんでした。

ということで2入力1出力のDEAに関してはこんな感じで文字を使って定式化することができました。より一般に\(m\)入力\(s\)出力の時も同じように考えることができます。第3章で実際に定式化していきましょう。

ここまでの話でDEAって何をしているのか、どうやって考えるのかのイメージが何となくわかったと思います。そこでこの章では\(m\)入力\(s\)出力、DMUの数が\(n\)個のDEAを分数計画問題として定式化していきす。

と言っても考え方はこれまでと同じなのでスムーズに理解できると思います。

もし\(\text{DMU}_1\)の効率値を計算したければ目的関数を \(o=1\) にすれば良いです。

ということでDEAを分数計画問題として定式化することができました。でも分数なんですよね。このままだと分数関数を持つ非線形計画問題を解かないといけないんです、嫌ですよね。

なんですが実はこの分数計画問題は線形計画問題に式変形することができるんです！第4章ではどうやって線形計画問題に変形するのかを紹介したいと思います。

それでは分数計画問題として定式化したDEAを線形計画問題に式変形していきましょう。式変形をするために新たに3つの文字 \(t,\mu_r,\nu_i\) を下記のように定義します。

\(t=\frac{1}{\sum\limits_{i=1}^m v_{i}x_{io}}, \; \mu_r = tu_r, \; \nu_i = tv_i\)

\(t\) は目的関数の分母の逆数を表しています。上の3つの文字を使うと目的関数は下記のように式変形をすることができます。

\((目的関数)=\frac{\sum\limits_{r=1}^s u_ry_{ro}}{\sum\limits_{i=1}^m v_{i}x_{io}} = t\sum\limits_{r=1}^s u_ry_{ro} = \sum\limits_{r=1}^s (tu_r)y_{ro}=\sum\limits_{r=1}^s \mu_ry_{ro}\)

ということで目的関数を線形関数に変形することができました。（\(u\)が\(\mu\)に変わったことに気を付けてください。）

次に制約条件を式変形してみます。

\(\frac{\sum\limits_{r=1}^s u_ry_{rj}}{\sum\limits_{i=1}^m v_{i}x_{ij}}\leq 1\)
\(\Leftrightarrow\sum\limits_{r=1}^s u_ry_{rj} \leq \sum\limits_{i=1}^m v_{i}x_{ij}\) (両辺に分母を掛けた)
\(\Leftrightarrow t\sum\limits_{r=1}^s u_ry_{rj} \leq t\sum\limits_{i=1}^m v_{i}x_{ij}\) (両辺に\(t\)を掛けた)
\(\Leftrightarrow \sum\limits_{r=1}^s (tu_r)y_{rj} \leq \sum\limits_{i=1}^m (tv_{i})x_{ij}\) (\(t\)をΣの中に入れた)
\(\Leftrightarrow \sum\limits_{r=1}^s \mu_ry_{rj} \leq \sum\limits_{i=1}^m \nu_{i}x_{ij}\) (\(u\)を\(\mu\)に、\(v\)を\(\nu\)に変換した)
\(\Leftrightarrow \sum\limits_{r=1}^s \mu_ry_{rj}-\sum\limits_{i=1}^m \nu_{i}x_{ij} \leq 0\) (右辺を左辺に持ってきた)

ということで制約条件も線形関数に変形することができました。後は\(t=(\sum\limits_{i=1}^m v_{i}x_{io})^{-1}\) を下記のように式変形します。

\(t=\frac{1}{\sum\limits_{i=1}^m v_{i}x_{io}}\)
\(\Leftrightarrow t\sum\limits_{i=1}^m v_{i}x_{io} = 1\)
\(\Leftrightarrow \sum\limits_{i=1}^m (tv_{i})x_{io} = 1\)
\(\Leftrightarrow \sum\limits_{i=1}^m \nu_{i}x_{io} = 1\)

以上のことをまとめると下記のようにDEAを線形計画問題として定式化することができます。

それではここまで説明してきたDEAをpythonで実装していきましょう。pulpを使って下記のように実装することができます。各プログラムが何をやっているのかを一つずつ解説していきます。

import pulp

class DEA:
    def __init__(self, dmus: int, target: int, inputs: list], outputs: list]):
        # パラメータの設定
        self.n = dmus  # DMU数
        self.o = target  # 評価対象DMU
        self.s = len(outputs)  # 出力値の数
        self.m = len(inputs)  # 入力値の数
        self.x = inputs  # 入力値
        self.y = outputs  # 出力値

        # 最適化問題の定義
        self.model = pulp.LpProblem("DEA", pulp.LpMaximize)

        # 変数の設定
        self.set_variables()

        # 目的関数の設定
        self.set_objective()

        # 制約条件の設定
        self.set_constraints()

    def set_variables(self):
        """変数の設定"""
        self.nu = pulp.LpVariable.dicts("nu", range(self.m), lowBound=0, cat=pulp.LpContinuous)
        self.mu = pulp.LpVariable.dicts("mu", range(self.s), lowBound=0, cat=pulp.LpContinuous)

    def set_objective(self):
        """目的関数の設定"""
        self.model += pulp.lpSum(self.mu[r] * self.y[r][self.o] for r in range(self.s))

    def set_constraints(self):
        """制約条件の設定"""
        for j in range(self.n):
            self.model += pulp.lpSum(self.mu[r] * self.y[r][j] for r in range(self.s)) - \
                         pulp.lpSum(self.nu[i] * self.x[i][j] for i in range(self.m)) <= 0

        self.model += pulp.lpSum(self.nu[i] * self.x[i][self.o] for i in range(self.m)) == 1
        
    def solve(self):
        """最適化問題を解く"""
        self.model.solve(solver=pulp.PULP_CBC_CMD(msg=False))
        return self.model
    
    def get_results(self):
        """結果の表示"""
        print(f"DMU{self.o+1}の効率値: {pulp.value(self.model.objective)}")
        for j in range(self.m):
            print(f"入力{j}の係数: {pulp.value(self.nu[j])}")
        for r in range(self.s):
            print(f"出力{r}の係数: {pulp.value(self.mu[r])}")

def main():
    dmus = 5
    target = 0
    inputs = [[2.0, 3.0, 4.0, 5.0, 6.0], [20.0, 17.0, 18.0, 16.0, 10.0]]
    outputs = [[10.0, 10.0, 10.0, 10.0, 10.0]]
    dea = DEA(dmus, target, inputs, outputs)
    dea.solve()
    dea.get_results()

if __name__ == "__main__":
    main()

このコードで扱っている問題例は2入力1出力の説明で用いたものです。

それではコードが何を表しているのかを1つずつ解説したいと思います。

初期設定

class DEA:
    def __init__(self, dmus: int, target: int, inputs: list], outputs: list]):
        # パラメータの設定
        self.n = dmus  # DMU数
        self.o = target  # 評価対象DMU
        self.s = len(outputs)  # 出力値の数
        self.m = len(inputs)  # 入力値の数
        self.x = inputs  # 入力値
        self.y = outputs  # 出力値

        # 最適化問題の定義
        self.model = pulp.LpProblem("DEA", pulp.LpMaximize)

        # 変数の設定
        self.set_variables()

        # 目的関数の設定
        self.set_objective()

        # 制約条件の設定
        self.set_constraints()

今回はクラスを使ってDEAを定義してみました。「__init__」メソッドには初期設定を書いています。

線形計画問題として定式化したときに使用した文字 \(n,o,s,m,x,y\) もここで設定しています。このとき「self.」を付けることで他のメソッドでも「self.n」のような形で使用できるようにしています。

また

        # 最適化問題の定義
        self.model = pulp.LpProblem("DEA", pulp.LpMaximize)

この部分で最適化問題のモデルを作成しています。モデルの作成は「pulp.LpProblem」でできます。「”DEA”」がmodelの名前を表し、「pulp.LpMaximize」でモデルを最大化問題に設定しています。これ以降このモデルには「self.model」でアクセスできます。

        # 変数の設定
        self.set_variables()

        # 目的関数の設定
        self.set_objective()

        # 制約条件の設定
        self.set_constraints()

この部分では後に定義する「set_variables」「set_objective」「set_constraints」メソッドを呼び出しています。これらは順に変数、目的関数、制約条件の設定を行う関数です。詳しい説明はこの後行います。

変数の設定

    def set_variables(self):
        """変数の設定"""
        self.nu = pulp.LpVariable.dicts("nu", range(self.m), lowBound=0, cat=pulp.LpContinuous)
        self.mu = pulp.LpVariable.dicts("mu", range(self.s), lowBound=0, cat=pulp.LpContinuous)

この部分では変数を設定しています。第4章での説明の通り、DEAでは下記2種類の変数を用います。

「self.nu」は \(\nu_{i}\)を表します。pulpでは変数を作るとき「pulp.LpVariable」を使います。また変数がたくさんあるときは「.dict」を使うと便利です。括弧の中身は

「”nu”」: 変数名
「range(self.m)]」: 添字の集合（\(0,1,2,…,m-1\)）
「lowBound=0」：変数が取りうる最小値は0
「cat=pulp.LpContinuous」: 変数は連続変数

をそれぞれ表しています。「self.mu」は \(\mu_{r}\) を表します。書き方は「self.nu」と同じです。

※rangeは0から始まることに注意してください。

目的関数の設定

    def set_objective(self):
        """目的関数の設定"""
        self.model += pulp.lpSum(self.mu[r] * self.y[r][self.o] for r in range(self.s))

ここでは目的関数を設定しています。

目的関数を設定するためには、先ほど定義したモデル「self.model」に「+=」で関数の式を書けば良いです。

\(\sum\)は「pulp.lpSum()」で表すことができます。

\(\mu_ry_{ro}\) は「self.mu[r] * self.y[r][self.o]」で表すことができます。

\(\sum\limits_{r=1}^s\) は「pulp.lpSum( … for r in range(self.s))」で表すことができます。

制約条件の設定

    def set_constraints(self):
        """制約条件の設定"""
        for j in range(self.n):
            self.model += pulp.lpSum(self.mu[r] * self.y[r][j] for r in range(self.s)) - \
                         pulp.lpSum(self.nu[i] * self.x[i][j] for i in range(self.m)) <= 0

        self.model += pulp.lpSum(self.nu[i] * self.x[i][self.o] for i in range(self.m)) == 1

ここでは制約条件を設定しています。変数が0以上という制約は変数を作成したときに既に設定しているので、上2つの制約を設定しています。

2種類の制約があるのでそれぞれ解説したいと思います。

1つ目の制約

        for j in range(self.n):
            self.model += pulp.lpSum(self.mu[r] * self.y[r][j] for r in range(self.s)) - \
                         pulp.lpSum(self.nu[i] * self.x[i][j] for i in range(self.m)) <= 0

制約条件を設定するときも目的関数と同じように「self.model」に「+=」で式を追加すればOKです。ただ目的関数の時と違って制約条件は不等式、もしくは等式を書く必要があります。

書き方は目的関数の時と同様、\(\sum\limits_{r=1}^{s}\) が「pulp.lpSum( … for r in range(self.s))」、\(\mu_ry_{rj}\) が「self.mu[r] * self.y[r][j]」と書けます。\(\nu_{i}x_{ij}\) も同じように書けます。

        for j in range(self.n):
            self.model += pulp.lpSum(self.mu[r] * self.y[r][j] for r in range(self.s)) - pulp.lpSum(self.nu[i] * self.x[i][j] for i in range(self.m)) <= 0

2つ目の制約

        self.model += pulp.lpSum(self.nu[i] * self.x[i][self.o] for i in range(self.m)) == 1

こちらは2つ目の制約条件（目的関数の分母が1になるやつ）を設定しています。こちらも「pulp.lpSum」を使って表現しています。ここまでの説明が理解できていればスッと理解できると思います。

最適化問題を解く

    def solve(self):
        """最適化問題を解く"""
        self.model.solve(solver=pulp.PULP_CBC_CMD(msg=False))
        return self.model

この部分で最適化問題を解いています。最適化問題を解くにはこれまで目的関数、制約条件を追加してきたモデル「self.model」に「.solve」を適用すれば良いです。引数の「solver」でどのソルバーを使うかを指定できます。今回はCBCを設定しました。（なにも設定しなかったらデフォルトでCBCになります。）

「pulp.PULP_CBC_CMD」の引数の「msg」はコマンドライン上に最適化計算のログを表示するか省略するかを決められます。「msg=False」とすると表示が省略されます。表示したかったらTrueにしてください。

もっと深堀り！

pulpが対応しているソルバーはCBC以外にもSCIP, CPLEX, GUROBI, XPRESSなどがあります。特にSCIPは無料で使えるソルバーでぼくも過去に紹介記事を作成しています。もしよければこちらの記事も見てみてください！

2025年3月23日数理最適化ソルバーのSCIPとCBCの2つの間にどれくらい性能の差があるのかを巡回セールスマン問題を使って調べてみた

2025年4月12日【これでわかる！】最適化ソルバーのSCIPをPySCIPOptから呼び出して数理最適化問題を解く方法を解説してみた

結果の表示

    def get_results(self):
        """結果の表示"""
        print(f"DMU{self.o+1}の効率値: {pulp.value(self.model.objective)}")
        for j in range(self.m):
            print(f"入力{j}の係数: {pulp.value(self.nu[j])}")
        for r in range(self.s):
            print(f"出力{r}の係数: {pulp.value(self.mu[r])}")

この部分では最適化結果の表示を行っています。

目的関数の値や変数の値を取得したい場合は「pulp.value」が使えます。目的関数は先ほど定義したモデル「self.model」に「.objective」を付ければ取得できます。

また変数は「self.mu」「self.nu」をfor文で回して「pulp.value()」で囲めば良いです。

モデルを動かして結果を見る

def main():
    dmus = 5
    target = 0
    inputs = [[2.0, 3.0, 4.0, 5.0, 6.0], [20.0, 17.0, 18.0, 16.0, 10.0]]
    outputs = [[10.0, 10.0, 10.0, 10.0, 10.0]]
    dea = DEA(dmus, target, inputs, outputs)
    dea.solve()
    dea.get_results()

if __name__ == "__main__":
    main()

最後にこの部分では実際にサンプルデータをモデルに入力して、モデルを動かして解を取得しています。ここでの「dmus」「inputs」「outputs」は2入力1出力の例で紹介した問題例です。

    dea = DEA(dmus, target, inputs, outputs)

この部分でDEAクラスの初期化を行っています。（より厳密に言うとDEAクラスのインスタンスを作成しています。）
今回は「dea」と名付けました。

    dea.solve()

この部分で問題を解いています。この「.solve」はさっきDEAクラス内で定義した「solve」メソッドです。

    dea.get_results()

この部分で結果を取得しています。この「.get_results」はさっきDEAクラス内で定義した「get_results」メソッドです。

実際に最適化問題を解いてみよう！

それでは今作ったコードを実行して最適化問題を解いてみましょう。問題例は2入力1出力の説明で使用したものです。

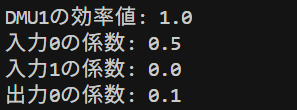
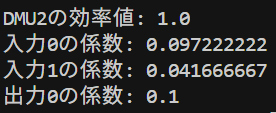
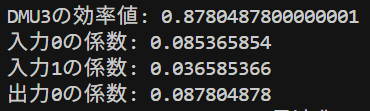
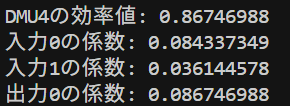
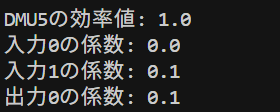
DMU1, DMU2, DMU5は効率値が1でした。DMU3の効率値は0.88、DMU4の効率値は0.87でした。2入力1出力の例の所で説明したのと同じ結果が得られましたね。


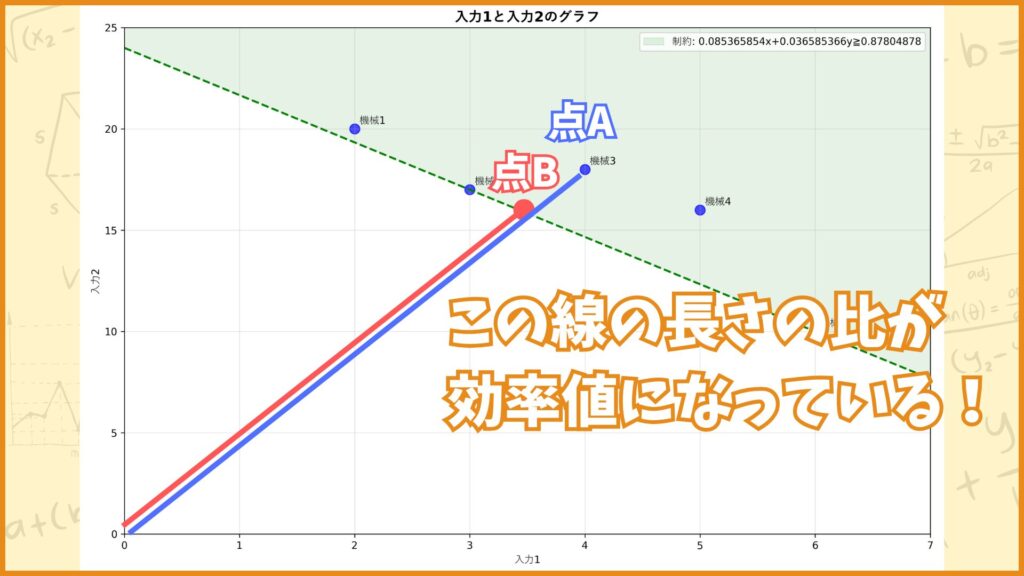
DMU3の効率値は0.8780…と1より小さい値ですが、これが何を表しているかをグラフを使って考えてみます。DMU3の点を点\(A\)、直線\(OA\)と緑点線の交点を点\(B\)としたときに、DMU3の効率値は

\(\frac{OB}{OA}\)

の値と一致するんです。図にすると下のようなイメージです。

実際に計算してみると

点A : \((4,18)\)
点B : \((3.5122,15.8049)\)
線分OAの長さ : \(18.4391\)
線分OBの長さ : \(16.1904\)
線分の長さの比 : \(0.8780\)

とちゃんとDMU3の効率値と一致していることが分かります。（pythonで計算したので若干の数値誤差はありますが。）

言い換えると「DMU3は入力値を点A(4,18)から点B(3.5122,15.8049)まで減らせば効率値が1になる」と言うことを表しています。このようにDEAではDMUが効率的じゃなかったときにどうすれば効率値を1にできるかまで計算することができます。

特に上の定式化では「出力値はそのままで入力値を減らして効率値を1に近づける」方法を教えてくれていますね。従ってこの定式化は入力指向のDEAになります。

実は今回紹介したDEAは

入力指向CRS乗数モデル

という数あるDEAのモデルの中の1種類でしかないんです。他にも色んなバリエーションがあるので、最後にそれらを簡単に紹介したいと思います。

入力指向と出力指向

今回紹介したモデルは上のような形でした。そしてこの定式化は「出力値はそのままで入力値を減らして効率値を1に近づける」入力指向の手法でした。

一方で「入力値はそのままで出力値を増やして効率値を1に近づける」モデルも存在します。こちらのモデルは出力指向と呼ばれ、下記のように定式化されます。

めっちゃ似ていますが

・分母と分子が逆になっている
・目的関数の最小化がターゲットになっている
・制約条件が1以上になっている

とよく見ると違う所がいくつかあります。出力指向のモデルでは効率値が1のDMUが効率的、1より大きいDMUが非効率的となります。

CRSとVRS

CRSってなに？

CRS（Constant Returns to Scale）は「規模の収穫一定」と言う意味で、入力を倍にすると出力も倍になることを表します。グラフにすると比例の直線で表されます。

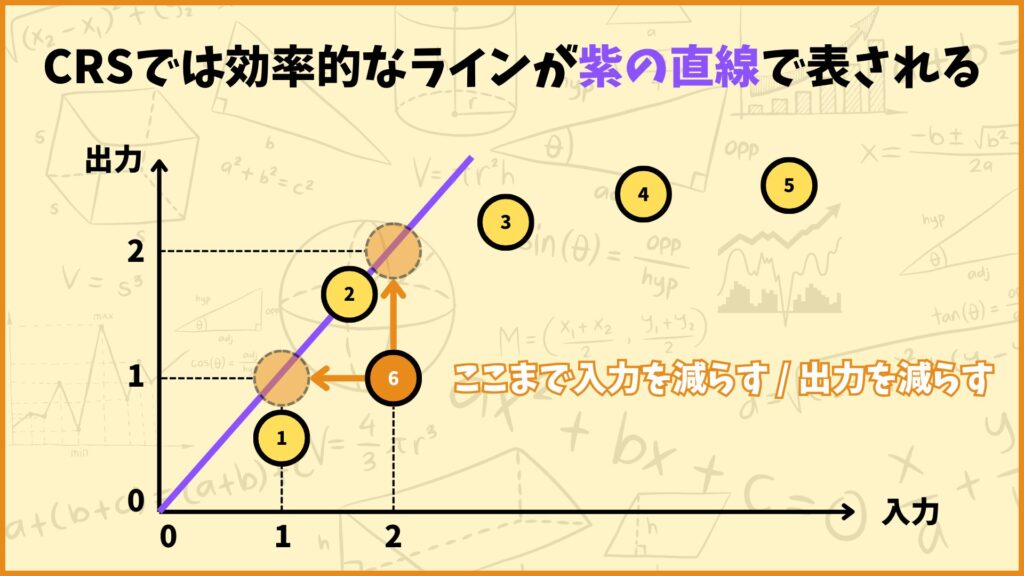
上図は1入力1出力のグラフで、紫の直線が効率的なラインを表しています。（これは第2章の1入力1出力の例で出てきましたね。）

この直線は規模の収穫一定を前提としています。仮に紫の効率的なラインが\(y=x\)で表されるとしましょう。（\(x\) : 入力, \(y\) : 出力）
このとき\((x,y)=(2,1)\)に位置するDMU6が効率的になるためには

入力値を\(2 \to 1\)に減らす or
出力値を\(1 \to 2\)に増やす

のいずれかをする必要があります。

これまでずっと話してきたモデルはCRSモデルなので、定式化したものは同じです。

VRSってなに？

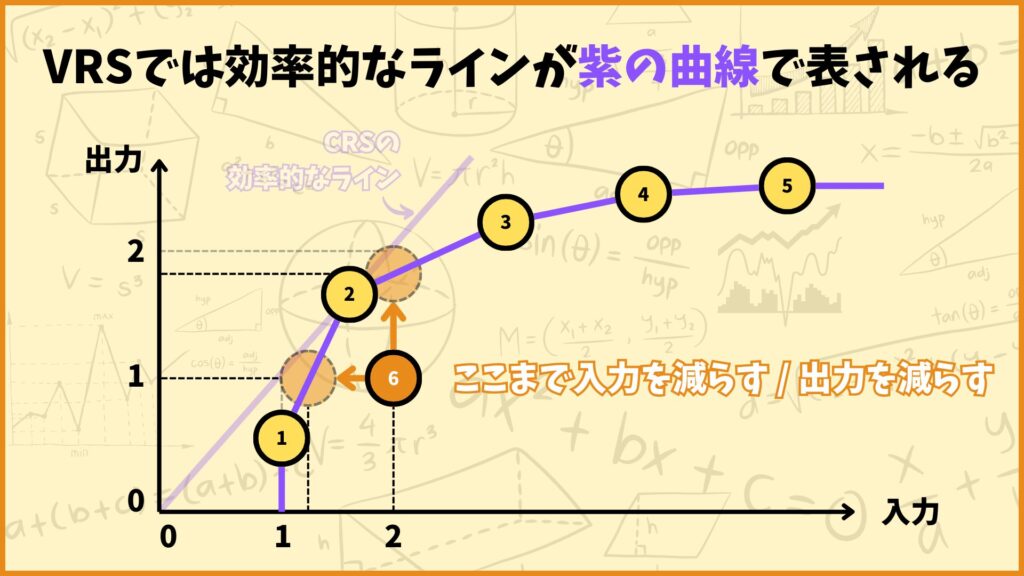
一方VRS（Variable Returns to Scale）は「規模の収穫可変」と言う意味で、入力を倍にすると出力も倍になるとは限らないことを表します。

CRSモデルでは原点と点2を結んだ直線が効率的フロンティアでしたが、VRSモデルでは上図のような折れ線が効率的フロンティアになります。さっきと同じようにDMU6が効率的になるためにはどれだけ入力を減らす/出力を増やせば良いか考えてみましょう。

入力を減らす場合、CRSモデルでは\(2\to1\)まで減らす必要がありましたが、VRSではだいたい\(1.2～1.3\)まで減らせば効率的フロンティアに達します。

一方出力を増やす場合、CRSモデルでは\(1\to2\)まで増やす必要がありましたが、VRSではだいたい\(1.7～1.8\)まで増やせば効率的フロンティアに達します。

VRSモデルは下記のように定式化することができます。

CRSと見比べると、変数 \(u_o\) が追加されています。この\(u _o\)は符号制約がない自由変数です。こちらもCRSモデルと同じように線形計画問題に変形することができます。

乗数モデルと包絡モデル

ここまで話してきたモデルは

\(\text{効率値} = \frac{\text{出力}}{\text{入力}}\)をどれだけ大きくできるか

に着目してモデルを考えていました。このようにして得られたモデルを乗数モデルと言います。

一方で下記のように定式化できる包絡モデルというDEAのモデルもあります。

包絡モデルが何を表しているかは別の記事で紹介したいと思います。（現在制作中です）

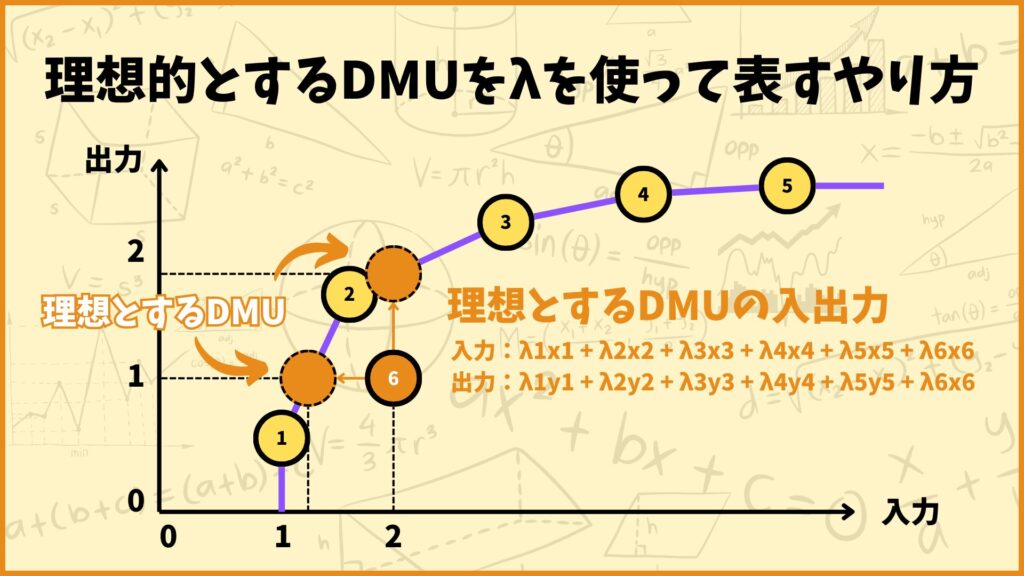
簡単に説明すると、理想とするDMUの入出力を実在するDMUの凸結合で表すやり方です。例えば上の例のようにDMUの数が6個だと、理想的なDMUの入出力は\(\lambda_j \; (j = 1,…,6)\)を使って

入力：\(\lambda_1x_{1}+\lambda_2x_{2}+\lambda_3x_{3}+\lambda_4x_{4}+\lambda_5x_{5}+\lambda_6x_{6}\)
出力：\(\lambda_1y_{1}+\lambda_2y_{2}+\lambda_3y_{3}+\lambda_4y_{4}+\lambda_5y_{5}+\lambda_6y_{6}\)

と表します。但し凸結合なので\(\sum\limits_{j=1}^n=1\)と言う制約が付きます。（この制約があるとVRSになります。）このような考え方に基づいて定式化したDEAが包絡モデルです。

今回はDEAを紹介しました！

今後もこのような組合せ最適化に関する記事を書いていきます！

最後までこの記事を読んでくれてありがとうございました。