- データ包絡分析法(DEA)ってなに?
- DEA(包絡モデル)に登場する数式の意味を理解したい…
- DEA(包絡モデル)をpythonで実装したい…
- 包絡モデルと乗数モデルの関係は?
こんにちは!しゅんです!
この記事ではデータ包絡分析法(DEA)について解説したいと思います!
DEAを数理計画問題として定式化する方法はいくつかあって、例えば下記のような定式化があります。
乗数モデル(前回の記事で紹介したやつ)
目的関数(\(\text{DMU}_{o}\)の効率値の最大化):
\(\frac{\sum\limits_{r=1}^s u_ry_{ro}}{\sum\limits_{i=1}^m v_{i}x_{io}}\)
制約条件:
\(\frac{\sum\limits_{r=1}^s u_ry_{rj}}{\sum\limits_{i=1}^m v_{i}x_{ij}}\leq 1 \;\;\; (j=1,…,n)\)
\(u_r \geq 0 \;\;\; (r = 1,…,s)\)
\(v_i \geq 0 \;\;\; (i = 1,…,m)\)
包絡モデル(この記事で紹介するやつ)
目的関数(\(\text{DMU}_o\)の\(\theta\)の最小化):
\(\theta\)
制約条件:
\(\sum\limits_{j=1}^n\lambda_jx_{ij}\leq \theta x_{io} \;\;\; (i=1,…,m)\)
\(\sum\limits_{j=1}^n\lambda_jy_{rj}\geq y_{ro} \;\;\; (r=1,…,s)\)
\(\sum\limits_{j=1}^n\lambda_j=1\)
\(\lambda_j \geq 0 \;\;\; (j=1,..,n)\)
前回の記事では乗数モデルのDEAについて解説しました。今回の記事では包絡モデルのDEAを紹介したいと思います!
\\\ 前回の記事はこちらから! ///
それではやっていきましょう!
【Udemy講座公開のお知らせ】
このたびUdemyで数理最適化の講座を公開しました!この講座は「数理最適化を勉強してみたいけど数式が多くて難しい…」という方向けに、どうやって最適化問題を定式化すれば良いかを優しく丁寧に解説しています!
2入力1出力の例で考える
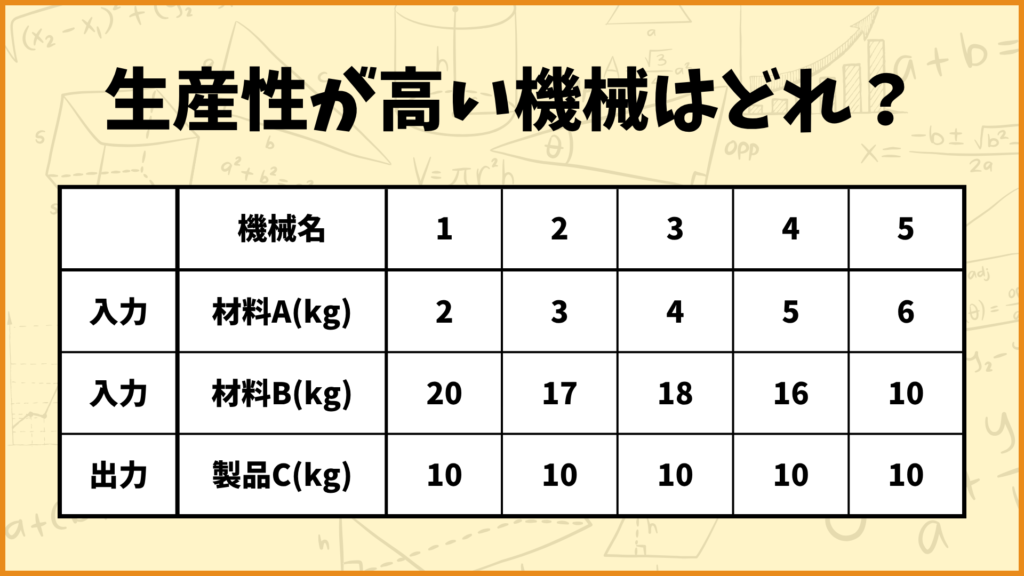
まず最初に2入力1出力の例を考えます。5つの機械があり、各機械は材料Aと材料Bを入力して製品Cを出力します。製品Cを10kg生産するのに必要な材料が上の表のようにまとめられています。
包絡モデルのポイントは「仮想的なDMU」をDMU1~DMU5を使って考えるということです。例えば
「機械1が30%、機械2が20%、機械3が10%、機械4が10%、機械5が30%の割合で組み合わせた“仮想的な機械”を考えてみよう。」
みたいな感じです。このとき仮想的な機械の入出力の値は下記のように計算されます。
材料A:\((0.3\times 2)+(0.2\times 3)+(0.1\times 4)+(0.1\times 5)+(0.3\times 6)=3.9\)
材料B:\((0.3\times 20)+(0.2\times 17)+(0.1\times 18)+(0.1\times 16)+(0.3\times 10)=15.8\)
製品C:\((0.3\times 10)+(0.2\times 10)+(0.1\times 10)+(0.1\times 10)+(0.3\times 10)=10\)
つまり、この割合で組み合わせた仮想的な機械は材料Aが3.9kg、材料Bが15.8kgで製品Cを10kg製造することができます。これはグラフにすると下のようになります。
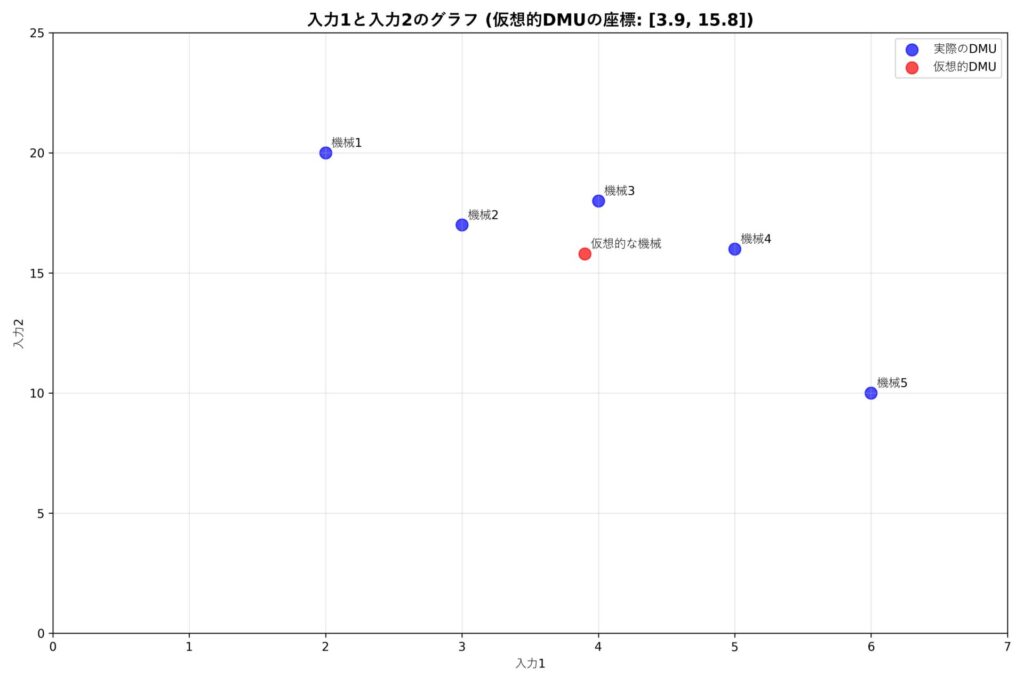
青点が機械1~5を表していて、赤点が先ほど計算した仮想的な機械を表しています。
このとき、仮想的な機械と機械3の入力値を比べてみると、材料Aの入力値は機械3が4kgなのに対して仮想的な機械が3.9kgと仮想的な機械の方が0.1kg少ないです。また材料Bの入力値は機械3が18kgなのに対して仮想的な機械が15.8kgと仮想的な機械の方が2.2kg少ないです。そして製品Cの出力値はどちらも10kgで同じです。
つまりこの仮想的な機械は機械3よりも少ない入力で同じ量の製品Cを出力するということが分かります。機械1~機械5の組合せで考えられる仮想的な機械の方が機械3よりも効率良く生産できるので、機械3は効率的ではないと考えられます。
逆に言えば機械3の無駄をもっと減らして材料Aを0.1kg、材料Bを2.2kg削減して製品Cを10kg作れるように改善すればこの仮想的な機械と同等の効率性を得られるという訳です。いわばこの仮想的な機械は機械3の改善目標みたいになります。
また、今は「機械1が30%、機械2が20%、機械3が10%、機械4が10%、機械5が30%」の組合せを考えていましたが、例えば「機械1が30%、機械2が20%、機械3が20%、機械4が10%、機械5が20%」の組合せを考えると、仮想的な機械の入力値はそれぞれ
材料A:\((0.3\times 2)+(0.2\times 3)+(0.2\times 4)+(0.1\times 5)+(0.2\times 6)=3.7\)
材料B:\((0.3\times 20)+(0.2\times 17)+(0.2\times 18)+(0.1\times 16)+(0.2\times 10)=16.6\)
となり、この場合も機械3より仮想的な機械の方が効率的ですね。(材料Aが0.3kg、材料Bが1.4kg少ない)
逆に言えば機械3の無駄をもっと減らして材料Aを0.3kg、材料Bを1.4kg削減して製品Cを10kg作れるように改善すればこの仮想的な機械と同等の効率性を得られるという訳です。この仮想的な機械も機械3の改善目標みたいになります。
では機械3は2つの仮想的な機械のうち、どっちを目標に改善していけば良いのでしょうか。そこで「入力をどれだけ一律に縮小できるか」を測る効率値 \(\theta\) を考えます。例えば前者の仮想的な機械は
材料A:\(\frac{3.9}{4}=0.975\)
材料B:\(\frac{15.8}{18}=0.877…\)
となるので、この仮想的な機械は機械3の \(\theta=0.975\) 倍の入力で同じだけの出力を出すことができると考えられます。
\(\theta\)は大きい方を採用します。その理由は、材料Aと材料Bの両方を同じ割合で縮小しなければならないからです。もし小さい方(0.877…)を採用してしまうと、材料Aは仮想的な機械が必要とする量よりもさらに少なくなってしまいます。
同じように後者の仮想的な機械についても効率値を考えると
材料A:\(\frac{3.7}{4}=0.925\)
材料B:\(\frac{16.6}{18}=0.922…\)
となるので、この仮想的な機械は機械3の \(\theta=0.925\) 倍の入力で同じだけの出力を出すことができると考えられます。従って2つの仮想的な機械を比べると、後者の方がより入力を少なくして同じだけの出力を出すことができるので後者の方がすごいということになります。
今は2つの仮想的な機械について考えましたが、本当は全ての割合の組合せを考えないといけません。そこで文字を使って考えます。仮想的な機械における機械 \(i\) の割合を \(\lambda_i\) とします。このとき各入出力値は\(\lambda\)を使って下記のように表すことができます。
材料A:\(2\lambda_1+3\lambda_2+4\lambda_3+5\lambda_4+6\lambda_5\)
材料B:\(20\lambda_1+17\lambda_2+16\lambda_3+18\lambda_4+10\lambda_5\)
製品C:\(10\lambda_1+10\lambda_2+10\lambda_3+10\lambda_4+10\lambda_5 \; (=10)\)
(\(\lambda\)には\(\lambda_1+\lambda_2+\lambda_3+\lambda_4+\lambda_5=1\)という制約があります。)
そして入力は機械3の入力値の \(\theta\) 倍以下になってほしいので下記の条件式が成り立ってほしいです。
材料A:\(2\lambda_1+3\lambda_2+4\lambda_3+5\lambda_4+6\lambda_5 \leq 4\theta\)
材料B:\(20\lambda_1+17\lambda_2+16\lambda_3+18\lambda_4+10\lambda_5 \leq 18\theta\)
出力に関しては機械3の出力値10を下回ってしまうと困るので
製品C:\(10\lambda_1+10\lambda_2+10\lambda_3+10\lambda_4+10\lambda_5 \geq 10\)
が成り立ってほしいです。(左辺が必ず10になるのでこの式は必ず満たされます。)
この条件を満たす中で、なるべく \(\theta\) を小さくすることを考えます。すなわち目的関数を \(\theta\) の最小化にします。これをまとめると下記の線形計画問題として定式化することができます。
目的関数(最小化):
\(\theta\)
制約条件:
\(2\lambda_1+3\lambda_2+4\lambda_3+5\lambda_4+6\lambda_5 \leq 4\theta\)
\(20\lambda_1+17\lambda_2+16\lambda_3+18\lambda_4+10\lambda_5 \leq 18\theta\)
\(10\lambda_1+10\lambda_2+10\lambda_3+10\lambda_4+10\lambda_5 \geq 10\)
\(\lambda_1+\lambda_2+\lambda_3+\lambda_4+\lambda_5=1\)
上の定式化は具体的な入出力値が分かっているときのものです。より一般に入出力値を\(x,y\)と表した時の定式化を考えます。
パラメータ:
\(x_{1j}\) : \(\text{DMU}_j\)の入力1(材料A)の値
\(x_{2j}\) : \(\text{DMU}_j\)の入力2(材料B)の値
\(y_{1j}\) : \(\text{DMU}_j\)の出力1(製品C)の値
変数:
\(\lambda_j\) : \(\text{DMU}_j\)の重み
\(\theta\) : \(\text{DMU}_o\)の効率値
目的関数(最小化):
\(\theta\)
制約条件:
\(\sum\limits_{j=1}^5\lambda_{j}x_{1j} \leq \theta x_{1o}\) (入力1の制約)
\(\sum\limits_{j=1}^5\lambda_{j}x_{2j} \leq \theta x_{2o}\) (入力2の制約)
\(\sum\limits_{j=1}^5\lambda_{j}y_{1j} \geq y_{io}\) (出力1の制約)
\(\sum\limits_{j=1}^{5}\lambda{j} = 1\)
包絡モデルを線形計画問題として定式化しよう!
これまでは入力値が2つ、出力値が1つ、DMUの数が5個の例をずっと考えてきました。ここからはより一般に
\(m\) 個の入力
\(s\) 個の出力
\(n\) 個のDMU
の場合の包絡モデルについて考えていきます。と言っても考え方は2入力1出力の時と同じです。
まず入力 \(i\) の制約について考えてみます。\(\text{DMU}_j\)の重みを \(\lambda_j\) とするとき、仮想的なDMUの入力 \(i\) の値は
\(\lambda_1x_{i1}+\lambda_2x_{i2}+\cdots+\lambda_{n}x_{in}=\sum\limits_{j=1}^{n}\lambda_{j}x_{ij}\)
と表せます。これが\(x_{io}\)の\(\theta\)倍以下になるという制約を考えれば良いので、下記の不等式で表すことができます。
\(\sum\limits_{j=1}^{n}\lambda_{j}x_{ij} \leq \theta x_{io}\)
これが全ての入力 \(i=1,…,m\) に対して成り立つというのが入力値に関する制約になります。
続いて出力 \(r\) の制約について考えてみます。こちらも\(\text{DMU}_j\)の重みを \(\lambda_j\) とするとき、仮想的なDMUの出力 \(r\) の値は
\(\lambda_1y_{r1}+\lambda_2y_{r2}+\cdots+\lambda_{n}y_{rn}=\sum\limits_{j=1}^{n}\lambda_{j}y_{rj}\)
と表せます。これが\(y_{ro}\)以上になるという制約を考えれば良いので、下記の不等式で表すことができます。
\(\sum\limits_{j=1}^{n}\lambda_{j}y_{rj} \geq y_{ro}\)
これが全ての出力 \(r=1,…,s\) に対して成り立つというのが出力値に関する制約になります。
最後に重み\(\lambda\)に関する制約を考えます。こちらは単純に総和が1になるという制約を考えれば良いので下記の等式で表すことができます。
\(\sum\limits_{j=1}^{n}\lambda_{j}=1\)
以上のことをまとめると、包絡モデルのDEAは下記の線形計画問題で定式化することができます。
パラメータ:
\(x_{ij}\) : \(\text{DMU}_j\)の入力 \(i\) の値
\(y_{rj}\) : \(\text{DMU}_j\)の出力 \(r\) の値
変数:
\(\lambda_j\) : \(\text{DMU}_j\)の重み
\(\theta\) : \(DMU_o\)の効率値
目的関数(最小化):
\(\theta\)
制約条件:
\(\sum\limits_{j=1}^n\lambda_jx_{ij}\leq \theta x_{io} \;\;\; (i=1,…,m)\)
\(\sum\limits_{j=1}^n\lambda_jy_{rj}\geq y_{ro} \;\;\; (r=1,…,s)\)
\(\sum\limits_{j=1}^n\lambda_j=1\)
\(\lambda_j \geq 0 \;\;\; (j=1,..,n)\)
ということでこんな感じで包絡モデルのDEAを定式化することができました。
今回は「同じ出力で入力を減らす」という方針でDMUの効率値を考えたのでこれは入力指向DEAモデルとなります。これとは対照的に「同じ入力で出力を増やす」という方針でDMUの効率値を考えることもできます。こちらは出力指向DEAモデルとなります。似たような考え方で下記のように出力指向DEAモデルを定式化することができます。
目的関数(最大化):
\(\phi\)
制約条件:
\(\sum\limits_{j=1}^n\lambda_jx_{ij}\leq x_{io} \;\;\; (i=1,…,m)\)
\(\sum\limits_{j=1}^n\lambda_jy_{rj}\geq \phi y_{ro} \;\;\; (r=1,…,s)\)
\(\sum\limits_{j=1}^n\lambda_j=1\)
\(\lambda_j \geq 0 \;\;\; (j=1,..,n)\)
この場合効率値\(\theta\)は「どれだけ出力値を大きくできるか」を表します。
包絡モデルをpythonで実装しよう!
それでは先ほどの定式化をpythonで実装して実際にDEAを解いてみましょう。まず最初にコードの全貌を見せた後、書く関数の説明を行いたいと思います。
コードの全貌
import pulp
class DEA:
def __init__(self, dmus: int, target: int, inputs: list, outputs: list):
# パラメータの設定
self.n = dmus # DMU数
self.o = target # 評価対象DMU
self.s = len(outputs) # 出力値の数
self.m = len(inputs) # 入力値の数
self.x = inputs # 入力値
self.y = outputs # 出力値
# 最適化問題の定義
self.model = pulp.LpProblem("DEA", pulp.LpMinimize)
# 変数の設定
self.set_variables()
# 目的関数の設定
self.set_objective()
# 制約条件の設定
self.set_constraints()
def set_variables(self):
"""変数の設定"""
self.lambdas = pulp.LpVariable.dicts("lambdas", range(self.n), lowBound=0, cat=pulp.LpContinuous)
self.theta = pulp.LpVariable("theta", cat=pulp.LpContinuous)
def set_objective(self):
"""目的関数の設定"""
self.model += self.theta
def set_constraints(self):
"""制約条件の設定"""
for i in range(self.m):
self.model += pulp.lpSum(self.lambdas[j] * self.x[i][j] for j in range(self.n)) <= self.theta * self.x[i][self.o]
for r in range(self.s):
self.model += pulp.lpSum(self.lambdas[j] * self.y[r][j] for j in range(self.n)) >= self.y[r][self.o]
self.model += pulp.lpSum(self.lambdas[j] for j in range(self.n)) == 1
def solve(self):
"""最適化問題を解く"""
self.model.solve(solver=pulp.PULP_CBC_CMD(msg=False))
return self.model
def get_results(self):
"""結果の表示"""
print(f"DMU{self.o+1}の効率値: {pulp.value(self.model.objective)}")
for j in range(self.n):
print(f"DMU{j+1}の係数: {pulp.value(self.lambdas[j])}")
def main():
dmus = 5
target = 0
inputs = [[2.0, 3.0, 4.0, 5.0, 6.0], [20.0, 17.0, 18.0, 16.0, 10.0]]
outputs = [[10.0, 10.0, 10.0, 10.0, 10.0]]
dea = DEA(dmus, target, inputs, outputs)
dea.solve()
dea.get_results()
if __name__ == "__main__":
main()
このコードで扱っている問題例は2入力1出力の説明で用いたものです。

それではコードが何を表しているのかを1つずつ解説したいと思います。
初期設定
class DEA:
def __init__(self, dmus: int, target: int, inputs: list, outputs: list):
# パラメータの設定
self.n = dmus # DMU数
self.o = target # 評価対象DMU
self.s = len(outputs) # 出力値の数
self.m = len(inputs) # 入力値の数
self.x = inputs # 入力値
self.y = outputs # 出力値
# 最適化問題の定義
self.model = pulp.LpProblem("DEA", pulp.LpMinimize)
# 変数の設定
self.set_variables()
# 目的関数の設定
self.set_objective()
# 制約条件の設定
self.set_constraints()
今回はクラスを使ってDEAを定義してみました。「__init__」メソッドには初期設定を書いています。
__init__メソッドの引数
dmus : DMUの数(int)
target : 効率値を求めたいDMU(int)
inputs : 入力値(2次元リスト)
outputs : 出力値(2次元リスト)
線形計画問題として定式化したときに使用した文字 \(n,o,s,m,x,y\) もここで設定しています。このとき「self.」を付けることで他のメソッドでも「self.n」のような形で使用できるようにしています。
\(\mu,\nu\) の2文字は「変数の設定」の所で設定しています。
また
# 最適化問題の定義
self.model = pulp.LpProblem("DEA", pulp.LpMinimize)この部分で最適化問題のモデルを作成しています。モデルの作成は「pulp.LpProblem」でできます。「”DEA”」がmodelの名前を表し、「pulp.LpMaximize」でモデルを最大化問題に設定しています。これ以降このモデルには「self.model」でアクセスできます。
# 変数の設定
self.set_variables()
# 目的関数の設定
self.set_objective()
# 制約条件の設定
self.set_constraints()この部分では後に定義する「set_variables」「set_objective」「set_constraints」メソッドを呼び出しています。これらは順に変数、目的関数、制約条件の設定を行う関数です。詳しい説明はこの後行います。
変数の設定
def set_variables(self):
"""変数の設定"""
self.lambdas = pulp.LpVariable.dicts("lambdas", range(self.n), lowBound=0, cat=pulp.LpContinuous)
self.theta = pulp.LpVariable("theta", cat=pulp.LpContinuous)この部分では変数を設定しています。第3章での説明の通り、包絡モデルでは下記2種類の変数を用います。
変数:
\(\lambda_{j}\) : \(\text{DMU}_j\) の係数
\(\theta\) : 効率値
「self.lambdas」は \(\lambda_{j}\)を表します。pulpでは変数を作るとき「pulp.LpVariable」を使います。また変数がたくさんあるときは「.dict」を使うと便利です。括弧の中身は
「”lambdas”」: 変数名
「range(self.n)]」: 添字の集合(\(0,1,2,…,n-1\))
「lowBound=0」:変数が取りうる最小値は0
「cat=pulp.LpContinuous」: 変数は連続変数
をそれぞれ表しています。
「self.theta」は \(\theta\) を表します。書き方は「self.lambdas」と同じです。
※rangeは0から始まることに注意してください。
「upBound」を指定すれば変数の最大値を設定することもできます。また変数は連続変数だけでなく
LpContinuous:連続変数
LpInteger:整数変数
LpBinary:0-1変数
があり、用途によって使い分けることができます。
目的関数の設定
def set_objective(self):
"""目的関数の設定"""
self.model += self.thetaここでは目的関数を設定しています。
目的関数(最小化):
\(\theta\)
目的関数を設定するためには、先ほど定義したモデル「self.model」に「+=」で関数の式を書けば良いです。
今回は目的関数が \(\theta\) だけなので「self.theta」だけでOKです。
制約条件の設定
def set_constraints(self):
"""制約条件の設定"""
for i in range(self.m):
self.model += pulp.lpSum(self.lambdas[j] * self.x[i][j] for j in range(self.n)) <= self.theta * self.x[i][self.o]
for r in range(self.s):
self.model += pulp.lpSum(self.lambdas[j] * self.y[r][j] for j in range(self.n)) >= self.y[r][self.o]
self.model += pulp.lpSum(self.lambdas[j] for j in range(self.n)) == 1ここでは制約条件を設定しています。\(\lambda_j\geq 0\)という制約は変数を作成したときに既に設定しているので、残りの上3つの制約を設定しています。
制約条件:
\(\sum\limits_{j=1}^n\lambda_jx_{ij}\leq \theta x_{io} \;\;\; (i=1,…,m)\)
\(\sum\limits_{j=1}^n\lambda_jy_{rj}\geq y_{ro} \;\;\; (r=1,…,s)\)
\(\sum\limits_{j=1}^n\lambda_j=1\)
\(\lambda_j \geq 0 \;\;\; (j=1,..,n)\)
1つ目の制約
for i in range(self.m):
self.model += pulp.lpSum(self.lambdas[j] * self.x[i][j] for j in range(self.n)) <= self.theta * self.x[i][self.o]\(\sum\limits_{j=1}^n\lambda_jx_{ij}\leq \theta x_{io} \;\;\; (i=1,…,m)\)
制約条件を設定するときも目的関数と同じように「self.model」に「+=」で式を追加すればOKです。ただ目的関数の時と違って制約条件は不等式、もしくは等式を書く必要があります。
pulpで\(\sum\)を書きたいときは「pulp.lpSum」を使います。「pulp.lpSum(… for j in range(self.n))」で\(\sum\limits_{j=1}^{n}\)を表現することができます。また「self.lambdas[j] * self.x[i][j]」で\(lambda_j x_{ij}\)を表現することができます。
これが\(\theta x_{io}\)以下であるという制約を作りたいので「<= self.theta * self.x[i][self.o]」を右に書きます。
厳密に言えば「for j in range(self.n))」は\(j=0,1,…,n-1\)の範囲で回すので\(\sum\limits_{j=0}^{n-1}\)が正しい表現ですが、別に解には影響を与えないのでそこまで気にする必要はないです。解の表示の時に「j」ではなく「j+1」を出力すればOKです。
2つ目の制約
for r in range(self.s):
self.model += pulp.lpSum(self.lambdas[j] * self.y[r][j] for j in range(self.n)) >= self.y[r][self.o]\(\sum\limits_{j=1}^n\lambda_jy_{rj}\geq y_{ro} \;\;\; (r=1,…,s)\)
2つ目の制約も1つ目の制約と同じようにpulpで表現することができます。左辺はほぼ一緒ですが、右辺には\(\theta\)が無くなっていることに注意してください。
3つ目の制約
self.model += pulp.lpSum(self.lambdas[j] for j in range(self.n)) == 1\(\sum\limits_{j=1}^n\lambda_j=1\)
ここで3つ目の制約条件を設定しています。こちらも「pulp.lpSum」を使って表現しています。ここまでの説明が理解できていればスッと理解できると思います。
最適化問題を解く
def solve(self):
"""最適化問題を解く"""
self.model.solve(solver=pulp.PULP_CBC_CMD(msg=False))
return self.modelこの部分で最適化問題を解いています。最適化問題を解くにはこれまで目的関数、制約条件を追加してきたモデル「self.model」に「.solve」を適用すれば良いです。引数の「solver」でどのソルバーを使うかを指定できます。今回はCBCを設定しました。(なにも設定しなかったらデフォルトでCBCになります。)
「pulp.PULP_CBC_CMD」の引数の「msg」はコマンドライン上に最適化計算のログを表示するか省略するかを決められます。「msg=False」とすると表示が省略されます。表示したかったらTrueにしてください。
pulpが対応しているソルバーはCBC以外にもSCIP, CPLEX, GUROBI, XPRESSなどがあります。特にSCIPは無料で使えるソルバーでぼくも過去に紹介記事を作成しています。もしよければこちらの記事も見てみてください!
結果の表示
def get_results(self):
"""結果の表示"""
print(f"DMU{self.o+1}の効率値: {pulp.value(self.model.objective)}")
for j in range(self.n):
print(f"DMU{j+1}の係数: {pulp.value(self.lambdas[j])}")この部分では最適化結果の表示を行っています。
目的関数の値や変数の値を取得したい場合は「pulp.value」が使えます。目的関数は先ほど定義したモデル「self.model」に「.objective」を付ければ取得できます。
また変数は「self.lambdas」をfor文で回して「pulp.value()」で囲めば良いです。
pythonはインデックスが0から始まるため「self.o」ではなく「self.o+1」としています。
モデルを動かして結果を見る
def main():
dmus = 5
target = 0
inputs = [[2.0, 3.0, 4.0, 5.0, 6.0], [20.0, 17.0, 18.0, 16.0, 10.0]]
outputs = [[10.0, 10.0, 10.0, 10.0, 10.0]]
dea = DEA(dmus, target, inputs, outputs)
dea.solve()
dea.get_results()
if __name__ == "__main__":
main()最後にこの部分では実際にサンプルデータをモデルに入力して、モデルを動かして解を取得しています。ここでの「dmus」「inputs」「outputs」は2入力1出力の例で紹介した問題例です。
dea = DEA(dmus, target, inputs, outputs)この部分でDEAクラスの初期化を行っています。(より厳密に言うとDEAクラスのインスタンスを作成しています。)
今回は「dea」と名付けました。
dea.solve()この部分で問題を解いています。この「.solve」はさっきDEAクラス内で定義した「solve」メソッドです。
dea.get_results()この部分で結果を取得しています。この「.get_results」はさっきDEAクラス内で定義した「get_results」メソッドです。
実際に最適化問題を解いてみよう!
それでは今作ったコードを実行して最適化問題を解いてみましょう。問題例は2入力1出力の説明で使用したものです。

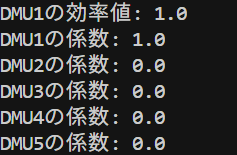
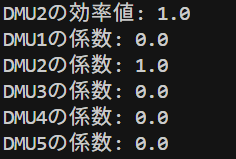
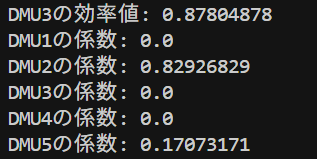
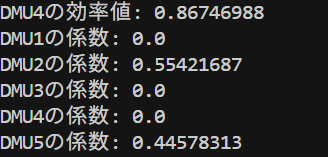
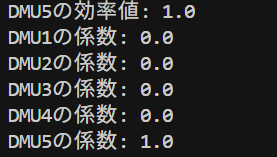
DMU1, DMU2, DMU5は効率値が1でした。DMU3の効率値は0.88、DMU4の効率値は0.87でした。この値は前回の記事で解説した乗数モデルのDEAと同じ値になっていますね。
\\\ 前回の記事はこちらから! ///
DMU3の効率値は0.8780…と1より小さい値ですが、これが何を表しているかをグラフを使って考えてみます。DMU3の点を点\(A\)、直線\(OA\)と緑点線の交点を点\(B\)としたときに、DMU3の効率値は
\(\frac{OB}{OA}\)
の値と一致するんです。図にすると下のようなイメージです。
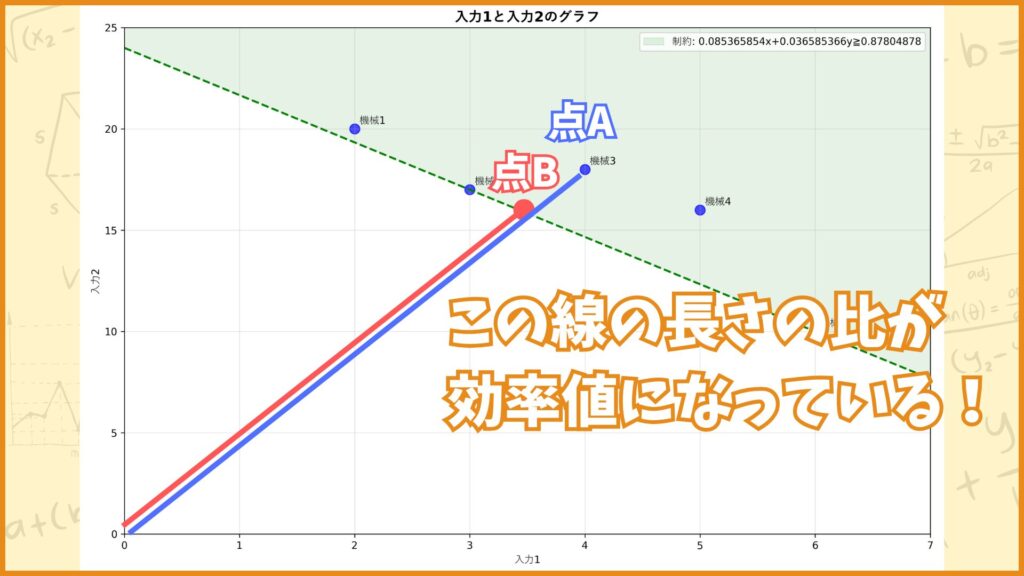
実際に計算してみると
点A : \((4,18)\)
点B : \((3.5122,15.8049)\)
線分OAの長さ : \(18.4391\)
線分OBの長さ : \(16.1904\)
線分の長さの比 : \(0.8780\)
とちゃんとDMU3の効率値と一致していることが分かります。(pythonで計算したので若干の数値誤差はありますが。)
言い換えると「DMU3は入力値を点A(4,18)から点B(3.5122,15.8049)まで減らせば効率値が1になる」と言うことを表しています。このようにDEAではDMUが効率的じゃなかったときにどうすれば効率値を1にできるかまで計算することができます。
特に上の定式化では「出力値はそのままで入力値を減らして効率値を1に近づける」方法を教えてくれていますね。従ってこの定式化は入力指向のDEAになります。
さらに各DMUの係数を見てみると
DMU2:0.829
DMU5:0.171
となっていて他の係数は0を取っていますね。つまりDMU3にとっての理想的な仮想的DMUの入出力は「DMU2が約82.9%、DMU5が約17.1%」だってことを表しています。例えば入力1は
\(\lambda_2^*x_{12}+\lambda_5^*x_{15}=0.82926829\times3 + 0.17073171\times6=3.51219513\)
と計算できます。図で考えると、仮にDMU2の点を点C、DMU5の点を点Dとする場合、理想的な仮想的DMU(点B)は線分CDを\(\lambda_2^*:\lambda_5^*\)に内分する点になっています。
包絡モデルと乗数モデルは双対関係がある
それでは最後に包絡モデルと乗数モデルの双対関係を考えていきます。包絡モデルを線形計画問題として定式化して、その双対問題を考えてみましょう。
包絡モデルを再掲しておきます。
包絡モデル
目的関数(\(\text{DMU}_o\)の\(\theta\)の最小化):
\(\theta\)
制約条件:
\(\sum\limits_{j=1}^n\lambda_jx_{ij}\leq \theta x_{io} \;\;\; (i=1,…,m)\)
\(\sum\limits_{j=1}^n\lambda_jy_{rj}\geq y_{ro} \;\;\; (r=1,…,s)\)
\(\sum\limits_{j=1}^n\lambda_j=1\)
\(\lambda_j \geq 0 \;\;\; (j=1,..,n)\)
また主問題と双対問題をベクトル\(c_1,b_1,x_1,y_1,c_2,b_2,x_2,y_2\)と行列\(A_{11},A_{12},A_{21},A_{22}\)を使ってそれぞれ表します。
主問題
目的関数(最小化)
\(c_1^{T}x_1 + c_2^{T}x_2\)
制約条件
\(A_{11}x_1+A_{12}x_2 \geq b_1\)
\(A_{21}x_1+A_{22}x_2 = b_2\)
\(x_1 \geq 0\)
双対問題
目的関数(最大化)
\(b_1^{T}y_1 + b_2^{T}y_2\)
制約条件
\(A_{11}^{T}y_1+A_{21}^Ty_2 \leq c_1\)
\(A_{12}^Ty_1+A_{22}^Ty_2 = c_2\)
\(y_1 \geq 0\)
まず包絡モデルをシグマを使わずに書きなおしてみます。
包絡モデル
目的関数(\(\text{DMU}_o\)の\(\theta\)の最小化):
\(\theta\)
制約条件:
\(-x_{11}\lambda_{1}-x_{12}\lambda_{2}-…-x_{1n}\lambda_{n}+x_{1o}\theta \geq 0\)
\(-x_{21}\lambda_{1}-x_{22}\lambda_{2}-…-x_{2n}\lambda_{n}+x_{2o}\theta \geq 0\)
…
\(-x_{m1}\lambda_{1}-x_{m2}\lambda_{2}-…-x_{mn}\lambda_{n}+x_{mo}\theta \geq 0\)
\(y_{11}\lambda_{1}+y_{12}\lambda_{2}+…+y_{1n}\lambda_{n} \geq y_{1o}\)
\(y_{21}\lambda_{1}+y_{22}\lambda_{2}+…+y_{2n}\lambda_{n} \geq y_{2o}\)
…
\(y_{s1}\lambda_{1}+y_{s2}\lambda_{2}+…+y_{sn}\lambda_{n} \geq y_{so}\)
\(\lambda_{1}+\lambda_{2}+…+\lambda_{n}=1\)
\(\lambda_{j} \geq 0\)
\(x_{ij},y_{rj}\)が係数で、\(\theta,\lambda_{j}\)が変数であることに注意してください。次に\(A_{11}\)だったり\(b_2\)とかがどんな値になるかを1個ずつ見ていきましょう。
\(A_{11}=\begin{pmatrix}-x_{11}&-x_{12}&\cdots&-x_{1n} \\ -x_{21}&-x_{22}&\cdots&-x_{2n} \\ \vdots&\vdots&\ddots&\vdots \\ -x_{m1}&-x_{m2}&\cdots&-x_{mn} \\ y_{11}&y_{12}&\cdots&y_{1n} \\y_{21}&y_{22}&\cdots&y_{2n} \\ \vdots&\vdots&\ddots&\vdots \\ y_{s1}&y_{s2}&\cdots&y_{sn} \end{pmatrix}, \; A_{12} = \begin{pmatrix} x_{1o} \\ x_{2o} \\ \vdots \\ x_{mo} \\ 0 \\ 0 \\ \vdots \\ 0 \end{pmatrix}\)
\(A_{21}=\begin{pmatrix} 1&1&\cdots&1 \end{pmatrix}, \; A_{22}=0\)
\(x_1 = \begin{pmatrix} \lambda_{1} \\ \lambda_{2} \\ \vdots \\ \lambda_{n} \end{pmatrix}, \; x_2 = \theta\)
\(b_1 = \begin{pmatrix} 0 \\ 0 \\ \vdots \\ 0 \\ y_{1o} \\ y_{2o} \\ \vdots \\ y_{so} \end{pmatrix}, \; b_2 = 1, \; c_1 = \begin{pmatrix}0\\0\\ \vdots \\ 0\end{pmatrix}, c_2 = 1\)
上のように表すことができます。それでは今度は双対問題を作ってみましょう。なおここで双対問題の変数\(y\)は下記の文字を使います。
\(y_1 = \begin{pmatrix}\nu_{1} \\ \nu_{2} \\ \vdots \\ \nu_{m} \\ \mu_{1} \\ \mu_{2} \\ \vdots \\ \mu_{s} \end{pmatrix}, \; y_2 = \mu_{o}\)
それでは双対問題の制約と目的関数を見ていきましょう。
目的関数: \(b_1^{T}y_1 + b_2^{T}y_2\)
\(y_{1o}\mu_1+y_{2o}\mu_2+\cdots+y_{so}\mu_{s}+\mu_{o}=\sum\limits_{r=1}^s\mu_{r}y_{ro}+\mu_{o}\)
制約条件: \(A_{11}^{T}y_1+A_{21}^Ty_2 \leq c_1\)
\(-x_{11}\nu_{1}-x_{21}\nu_{2}-\cdots-x_{m1}\nu_{m}+y_{11}\mu_{1}+y_{21}\mu_{2}+\cdots+y_{s1}\mu_{s}+\mu_{o}\leq 0\)
\(-x_{12}\nu_{1}-x_{22}\nu_{2}-\cdots-x_{m2}\nu_{m}+y_{12}\mu_{1}+y_{22}\mu_{2}+\cdots+y_{s2}\mu_{s}+\mu_{o}\leq 0\)
…
\(-x_{1n}\nu_{1}-x_{2n}\nu_{2}-\cdots-x_{mn}\nu_{m}+y_{1n}\mu_{1}+y_{2n}\mu_{2}+\cdots+y_{sn}\mu_{s}+\mu_{o}\leq 0\)
\(\Updownarrow\)
\(\sum\limits_{r=1}^s\mu_{r}y_{rj}-\sum\limits_{i=1}^m\nu_{i}x_{ij}+\mu_{o}\leq 0 \;\; (j = 1,2,…,n)\)
制約条件: \(A_{12}^Ty_1+A_{22}^Ty_2 = c_2\)
\(x_{1o}\nu_{1}+x_{2o}\nu_{2}+\cdots+x_{mo}\nu_{m}=1\)
\(\Updownarrow\)
\(\sum\limits_{i=1}^m\nu_{i}x_{io}=1\)
制約条件: \(y_1 \geq 0\)
\(\mu_r \geq 0 \;\; (r=1,2,…,s)\)
\(\nu_i \geq 0 \;\; (i=1,2,…,m)\)
ということで双対問題を作ることができました。まとめると下記のような双対問題になります。
目的関数(最大化):
\(\sum\limits_{r=1}^s \mu_ry_{ro}+\mu_o\)
制約条件:
\(\sum\limits_{r=1}^s \mu_ry_{rj}-\sum\limits_{i=1}^m \nu_{i}x_{ij}+\mu_o\leq 0 \;\;\; (j=1,…,n)\)
\(\sum\limits_{i=1}^m \nu_ix_{io}=1\)
\(\mu_r \geq 0 \;\;\; (r = 1,…,s)\)
\(\nu_i \geq 0 \;\;\; (i = 1,…,m)\)
\(\mu_o\)は符号条件なし
これ前回の記事で紹介したVRS乗数モデルになっていますよね。ということでDEAの包絡モデルと乗数モデルには双対関係があることが分かりました。
\\\ 前回の記事はこちらから! ///
ぼくたちがこの記事でずっと扱ってきた包絡モデルはVRS包絡モデルと呼ばれます。VRSは規模の収穫可変を表し、その他にCRS(規模の収穫一定)包絡モデルというのもあります。これはVRS包絡モデルの制約条件から\(\sum\limits_{j=1}^n\lambda_j=1\)を除いたものになります。
CRS包絡モデル
目的関数(\(\text{DMU}_o\)の\(\theta\)の最小化):
\(\theta\)
制約条件:
\(\sum\limits_{j=1}^n\lambda_jx_{ij}\leq \theta x_{io} \;\;\; (i=1,…,m)\)
\(\sum\limits_{j=1}^n\lambda_jy_{rj}\geq y_{ro} \;\;\; (r=1,…,s)\)
\(\lambda_j \geq 0 \;\;\; (j=1,..,n)\)
CRSの場合に関しても包絡モデルと乗数モデルで双対関係があります。
CRS乗数モデル
目的関数(\(\text{DMU}_{o}\)の効率値の最大化):
\(\sum\limits_{r=1}^s \mu_ry_{ro}\)
制約条件:
\(\sum\limits_{r=1}^s \mu_ry_{rj}-\sum\limits_{i=1}^m \nu_{i}x_{ij} \leq 0 \;\;\; (j=1,…,n)\)
\(\sum\limits_{i=1}^m \nu_{i}x_{io} = 1\)
\(\mu_r \geq 0 \;\;\; (r = 1,…,s)\)
\(\nu_i \geq 0 \;\;\; (i = 1,…,m)\)
おわりに
今回はDEAを紹介しました!
今後もこのような数理最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。