- 最短経路問題ってなに?
- ワーシャルフロイド法ってなに?
- ワーシャルフロイド法のアルゴリズムを知りたい…
こんにちは!しゅんです!
この記事ではワーシャルフロイド法について解説しています。
そもそもワーシャルフロイド法で何を求めることができるのか、アルゴリズムの手順は何なのかについてなるべく分かりやすく1つずつ丁寧に解説してみたいと思います!
それではやっていきましょう!
【Udemy講座公開のお知らせ】
このたびUdemyで数理最適化の講座を公開しました!この講座は「数理最適化を勉強してみたいけど数式が多くて難しい…」という方向けに、どうやって最適化問題を定式化すれば良いかを優しく丁寧に解説しています!
ワーシャルフロイド法ってどんなアルゴリズム?
ワーシャルフロイド法は重み付き有向グラフの全ての頂点ペア間の最短経路を多項式時間で求めることができるアルゴリズムです。
…と文字だけで説明されてもよく分からないので1つずつ丁寧に解説したいと思います。
最短経路問題ってなに?
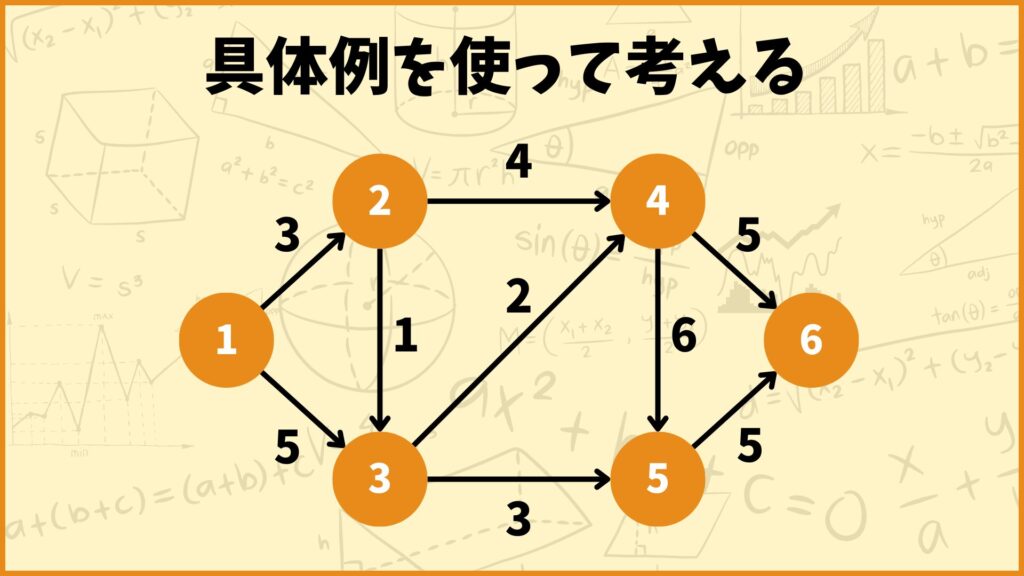
上図のグラフを使って最短経路問題について説明します。
グラフ理論におけるグラフとは上図のように頂点と辺から構成されます。辺に向きがある場合は有向グラフ、辺に重みがある場合は重み付きグラフなんて呼ばれたりします。
今回は辺に向きがあり、かつ辺に重みがあるので重み付き有向グラフなんて呼ばれたりします。
今自分が頂点1にいて、これから頂点6に向かうとします。辺の重みが2頂点間を移動するのにかかる時間(分)だと考えたときに、なるべく早く頂点6に到達できるルートを考えるのが最短経路問題です。
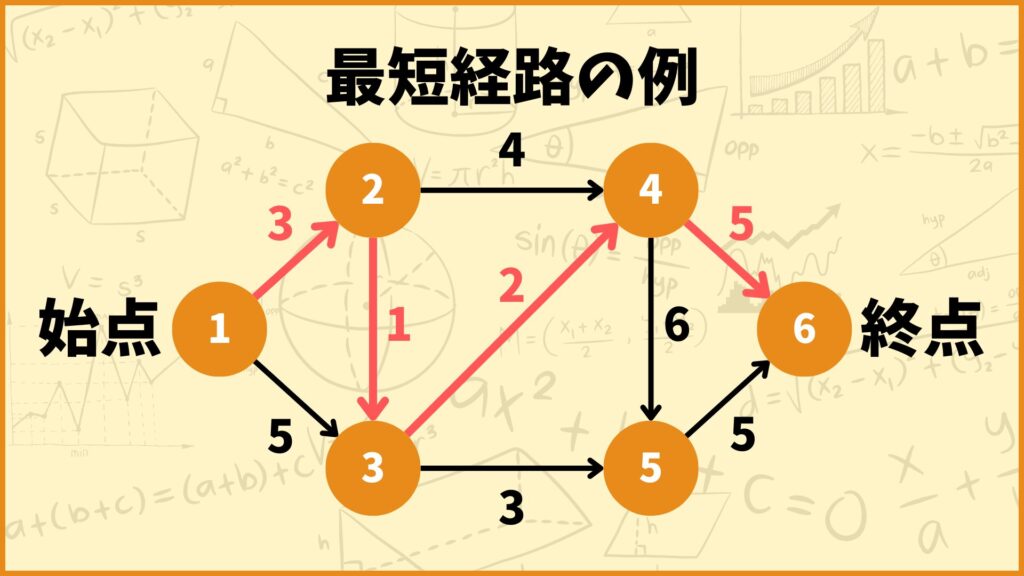
例えば頂点1→頂点2→頂点3→頂点4→頂点6というルートだと合計で3+1+2+5 = 11(分)かかります。実はこれがこのグラフにおける頂点1~頂点6間の最短経路となります。これを求めるのが最短経路問題です。
最短経路問題を解くアルゴリズムとして、例えばダイクストラ法やベルマンフォード法なんかが有名です。ダイクストラ法は辺の重みが非負である場合でしか使えない一方で、ベルマンフォード法は負の重みがあっても使えるなど違いはありますが、この記事では詳しい説明は省略します。
\\\ ダイクストラ法はこちらの記事で詳しく解説しています! ///
\\\ ベルマンフォード法はこちらの記事で解説しています! ///
ワーシャルフロイド法は全ての2頂点間の最短距離を求めるアルゴリズム
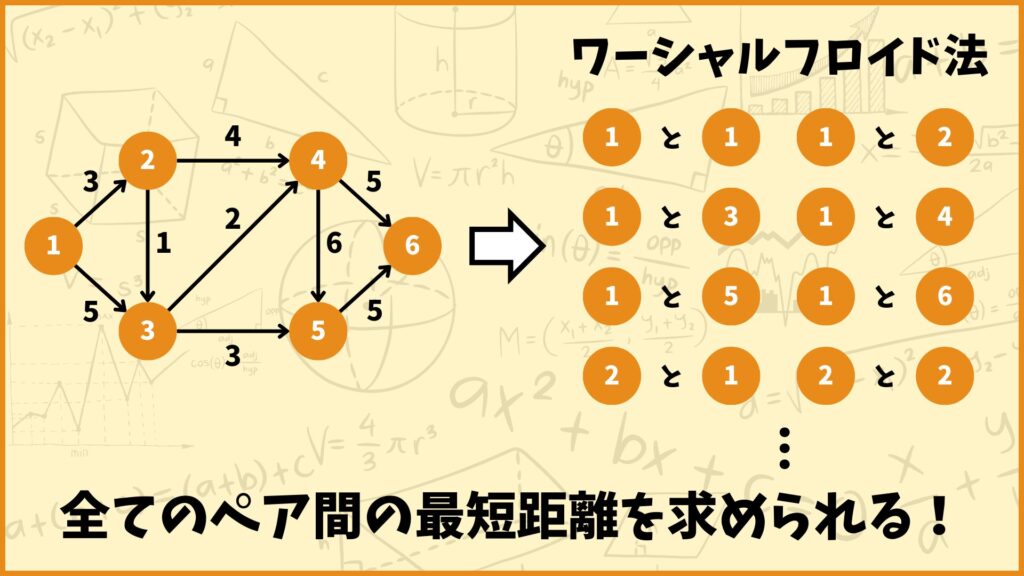
それでは次にワーシャルフロイド法が何を求めるアルゴリズムかについて説明します。先ほども述べたように、ワーシャルフロイド法は全ての2頂点間の最短距離を求めるアルゴリズムです。
「全ての2頂点間の」という所が先述のダイクストラ法やベルマンフォード法と違う所です。
ダイクストラ法やベルマンフォード法はどの2頂点間の最短距離を求めるかというのがあらかじめ与えられています。

先ほどの例だと頂点1を始点、頂点6を終点としたときの始点から終点までの最短距離を求めました。
ワーシャルフロイド法はそうじゃなくて、例えば頂点1~頂点4間の最短距離、頂点2~頂点5間の最短距離、頂点4~頂点5間の最短距離…といったように全ての頂点ペア間の最短距離を一気に求めることができます。
ワーシャルフロイド法の手順ってどんな感じ?
説明に使う記号の定義
まず最初にアルゴリズムの説明で使う記号の定義を行います。ワーシャルフロイド法を適用したい重み付き有向グラフを \(G = (V,E)\) とします。このとき頂点数を \(n\) とし、頂点の集合は \(V = \{1,2,…,n\}\) とします。
また\(d_{ij}^{(k)}\)を以下のように定義します。
\(d_{ij}^{(k)}\) の定義:
\(V\) の部分集合 \(\{1,2,…,k\}\) 中の頂点だけしか通れないときの、頂点 \(i\) から頂点 \(j\) への最短距離
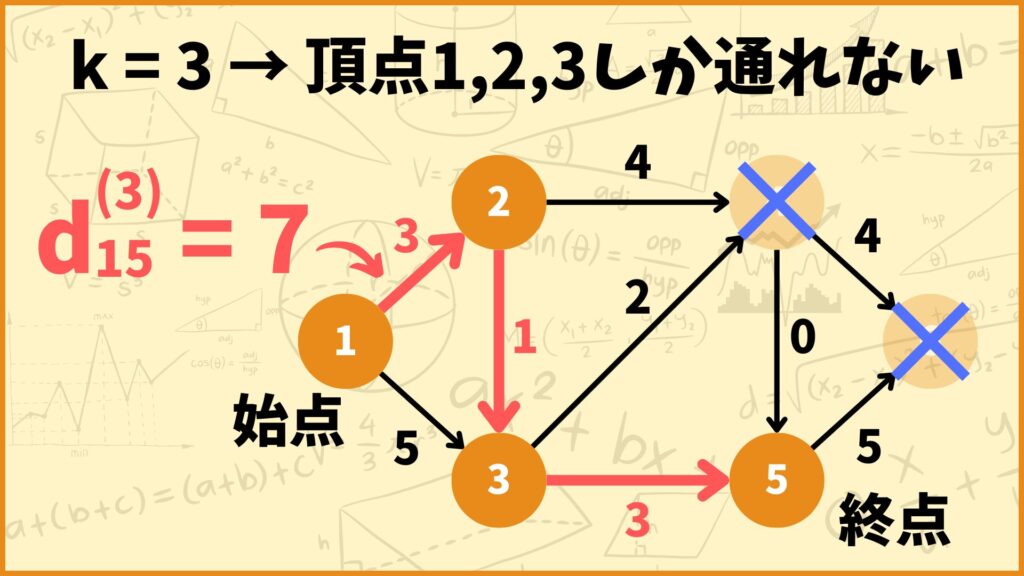
例えば上のグラフについて、頂点1から頂点5までの最短経路を考えてみましょう。\(k = 3\) としているので頂点 \(1,2,3\) しか通れません。このときの最短経路は頂点1→頂点2→頂点3→頂点5なので
\(d_{15}^{(3)} = 3 + 1 + 3 = 7\)
と計算できます。
\(k = n\) のときは全ての頂点を通ることができます。つまり \(d_{ij}^{(n)}\) は全ての頂点を通れる場合の頂点 \(i\) から頂点 \(j\) への最短距離となり、最終的に求めたいものとなります。
また \(d_{ij}^{(0)}\) を途中に通って良い頂点が一つもないときの頂点 \(i\) から頂点 \(j\) への最短距離を表すとします。このように考えると \(d_{ij}^{(0)}\) は辺 \((i,j)\) の重みと一致します。
なお辺 \((i,j)\) が存在しない場合は \(d_{ij}^{(0)}= \infty\) とします。
ワーシャルフロイド法の手順
結論ワーシャルフロイド法の手順は以下のようになります。
STEP 0 グラフの重み付き隣接行列を用意する。(最短距離の初期値 \(d_{ij}^{(0)}\) の設定)
STEP 1 \(k = 1\) とし、全ての \(i,j \in V\) に対して \(d_{ij}^{(1)}\) を以下のように更新する。
\(d_{ij}^{(1)} = \min\{d_{ij}^{(0)}, d_{i1}^{(0)} + d_{1j}^{(0)}\}\)
STEP 2 \(k = 2\) とし、全ての \(i,j \in V\) に対して \(d_{ij}^{(2)}\) を以下のように更新する。
\(d_{ij}^{(2)} = \min\{d_{ij}^{(1)}, d_{i2}^{(1)} + d_{2j}^{(1)}\}\)
STEP 3 \(k = 3\)とし、全ての \(i,j \in V\) に対して \(d_{ij}^{(3)}\) を以下のように更新する。
\(d_{ij}^{(3)} = \min\{d_{ij}^{(2)}, d_{i3}^{(2)} + d_{3j}^{(2)}\}\)
・
・
・
STEP n \(k = n\)とし、全ての \(i,j \in V\) に対して \(d_{ij}^{(n)}\) を以下のように更新する。
\(d_{ij}^{(n)} = \min\{d_{ij}^{(n-1)}, d_{in}^{(n-1)} + d_{nj}^{(n-1)}\}\)
…と文字だけで説明されてもよく分からないので具体例を使って1つずつ解説したいと思います。
具体例を使って説明する
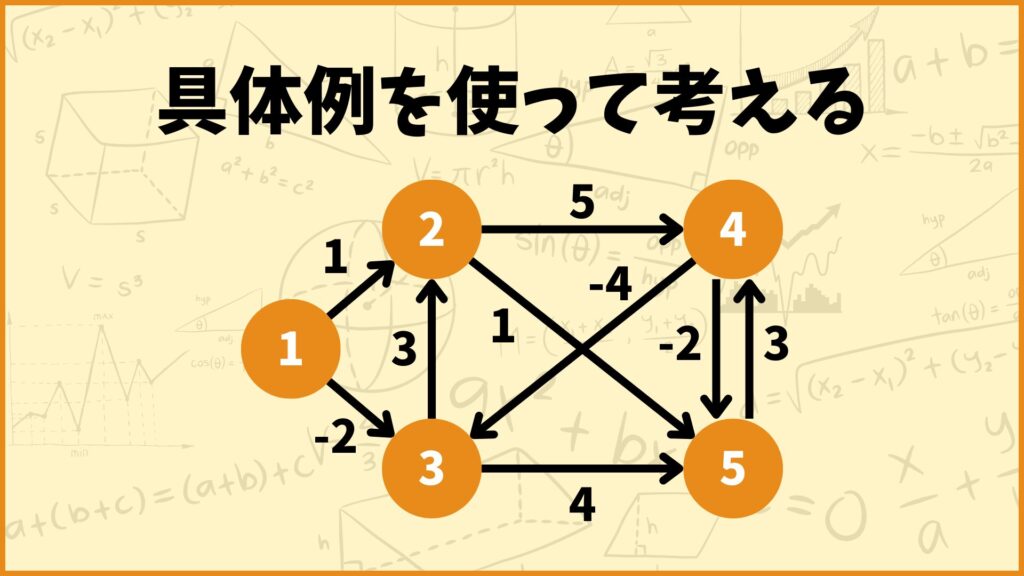
それでは上のグラフにワーシャルフロイド法を適用してみましょう。
STEP 0
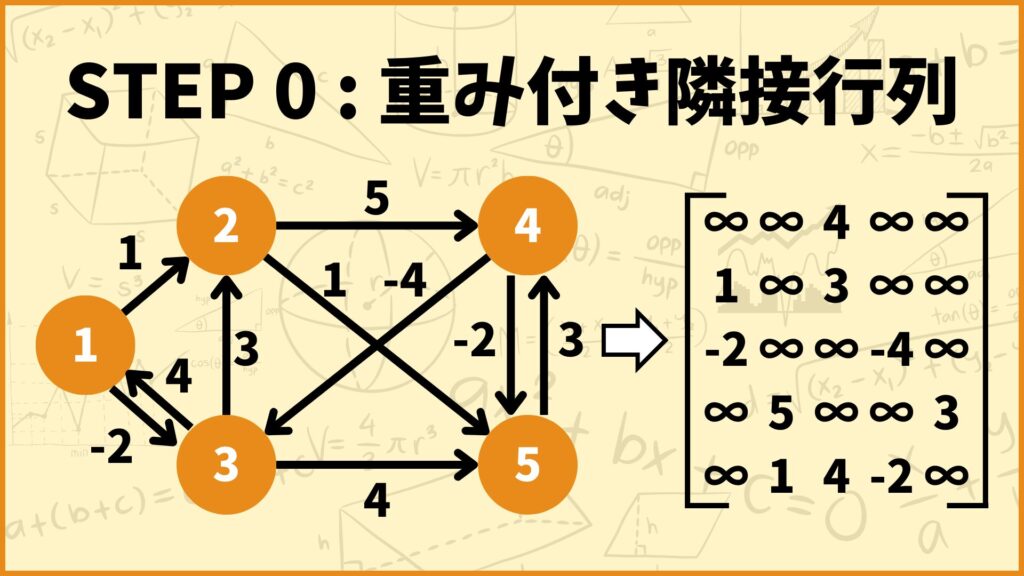
まず最初に重み付き隣接行列を用意します。グラフの頂点数が \(n\) だとすると重み付き隣接行列は \(n \times n\) の正方行列となり、また\((i,j)\) 成分は以下のように設定します。
辺 \((i,j)\) がある:辺 \((i,j)\) の重み
辺 \((i,j)\) がない:\(\infty\)
つまりこの行列の \((i,j)\) 成分は \(d_{ij}^{(0)}\) となります。
上のグラフで言うと例えば辺 \((2,4)\) の重みは5なので行列の \((2,4)\) 成分は5となります。逆に辺 \((1,4)\) は存在しないので行列の \((1,4)\) 成分は \(\infty\) となります。
\(d_{24}^{(0)}=5\)
\(d_{14}^{(0)}=\infty\)
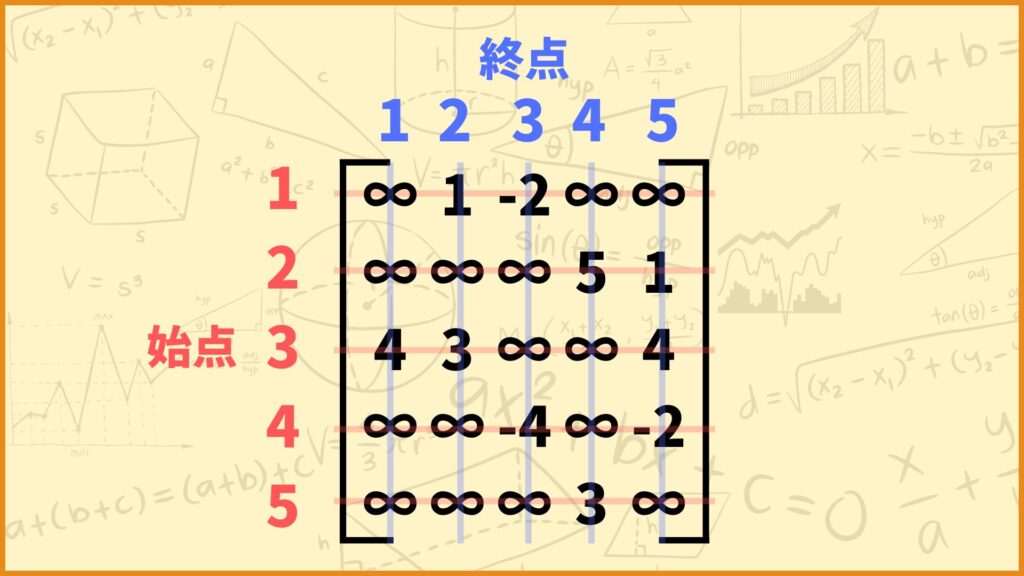
重み付き隣接行列は各行のインデックスが始点、各列のインデックスが終点を表しています。
STEP 1
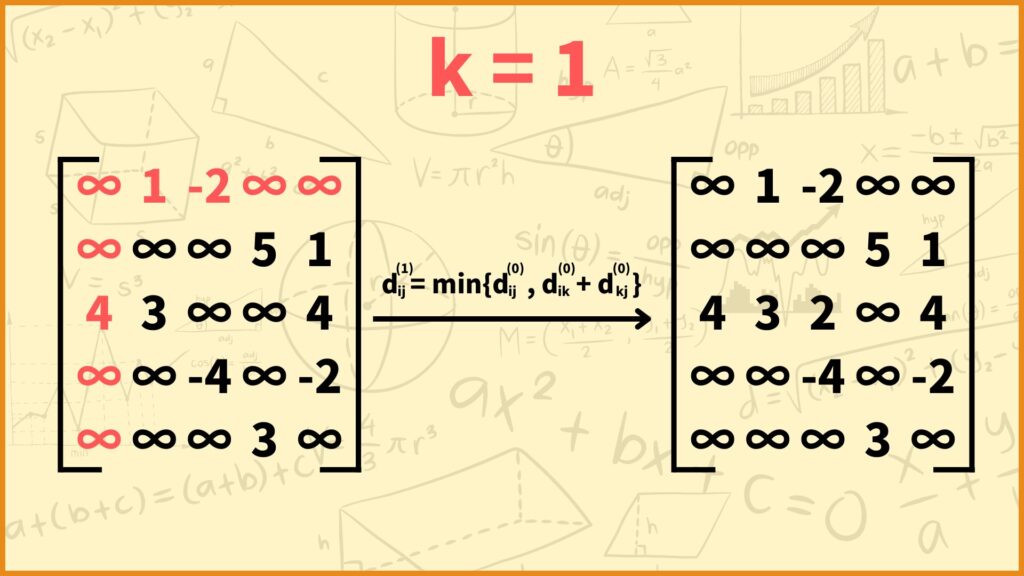
(上図の左側の行列の \((i,j)\) 成分は \(d_{ij}^{(0)}\) を表しており、右側の行列の \((i,j)\) 成分は \(d_{ij}^{(1)}\) を表しています。)
STEP 1では \(d_{ij}^{(1)}\)、つまり
「通って良い頂点が頂点1だけの場合における2頂点間の最短距離」
を求めていきます。下の式に従って \(d_{ij}^{(1)}\) の値を決めていけばOKです。
\(d_{ij}^{(1)} = \min\{d_{ij}^{(0)}, d_{i1}^{(0)} + d_{1j}^{(0)}\}\)
文字だけじゃ分かりづらいので例を挙げて説明します。\((i,j) = (3,3)\) について考えてみましょう。

STEP 0で
\(d_{33}^{(0)} = \infty\)
\(d_{31}^{(0)} = 4, d_{13}^{(0)} = -2\)
であることが分かっています。そのためあの式に従って \(d_{33}^{(1)}\) を計算すると
\(d_{33}^{(1)} = \min\{\infty, 4-2\} = 2\)
となります。
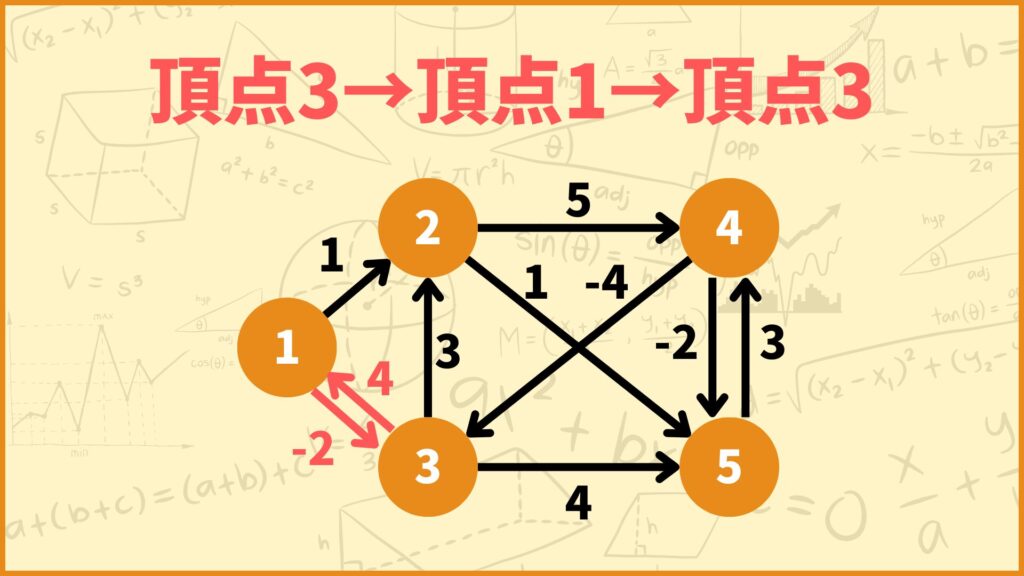
イメージとしては頂点3から直接頂点3に向かうルート(自己ループがないので重みは\(\infty\))よりも頂点1を経由する頂点3→頂点1→頂点3のルートの方が距離の合計が短いのでそっちを採用するみたいな感じです。
他には例えば \((i,j) = (4,2)\) について考えてみましょう。STEP 0より
\(d_{42}^{(0)} = \infty\)
\(d_{41}^{(0)} = \infty, d_{12}^{(0)} = 1\)
であることが分かっています。そのためさっきの式に従って \(d_{42}^{(1)}\) を計算すると
\(d_{42}^{(1)} = \min\{\infty, \infty+1\} = \infty\)
となります。このような計算を全てのマスで行うと下図の右の行列が得られると思います。

STEP 1で得られた行列の \((i,j)\) 成分は \(d_{ij}^{(1)}\) となっており、\(d_{ij}^{(1)}\) は頂点1しか通れないときの \(i\)~\(j\) 間の最短距離を表しています。つまりこの行列は
「全ての2頂点間における、頂点1しか通れないときの最短距離」
をまとめた行列となっているんです。
なぜ\(d_{ij}^{(1)} = \min\{d_{ij}^{(0)}, d_{i1}^{(0)} + d_{1j}^{(0)}\}\)が成り立つのかは下の記事で解説しています!
STEP 2
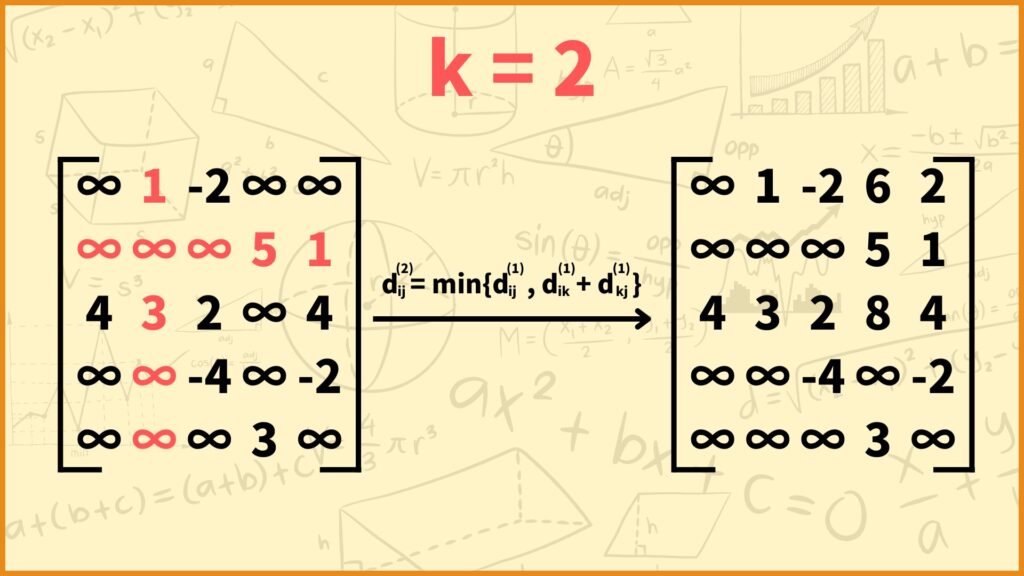
(上図の左側の行列の \((i,j)\) 成分は \(d_{ij}^{(1)}\) を表しており、右側の行列の \((i,j)\) 成分は \(d_{ij}^{(2)}\) を表しています。)
STEP 2では \(d_{ij}^{(2)}\)、つまり
「通って良い頂点が頂点1と頂点2の場合における2頂点間の最短距離」
を求めていきます。下の式に従って \(d_{ij}^{(2)}\) の値を決めていけばOKです。
\(d_{ij}^{(2)} = \min\{d_{ij}^{(1)}, d_{i2}^{(1)} + d_{2j}^{(1)}\}\)
STEP 1とほぼ同じ操作を行うので、変化があった成分だけ説明します。
始点:頂点1
\(d_{14}^{(2)} = \min\{d_{14}^{(1)}, d_{12}^{(1)} + d_{24}^{(1)}\}=\min\{\infty, 1+5\}=6\)
\(d_{15}^{(2)} = \min\{d_{15}^{(1)}, d_{12}^{(1)} + d_{25}^{(1)}\}=\min\{\infty, 1+1\}=2\)
始点:頂点3
\(d_{34}^{(2)} = \min\{d_{34}^{(1)}, d_{32}^{(1)} + d_{24}^{(1)}\}=\min\{\infty, 3+5\}=8\)
例えば \((i,j) = (1,4)\) について考えてみましょう。STEP 1より
\(d_{14}^{(1)} = \infty\)
\(d_{12}^{(1)} = 1, d_{24}^{(1)} = 5\)
であることが分かっています。そのためさっきの式に従って \(d_{42}^{(2)}\) を計算すると
\(d_{42}^{(2)} = \min\{\infty, 1+5\} = 6\)
となります。これは途中で通っても良い頂点が頂点1と頂点2のとき、頂点1~頂点4間の最短距離が6であることを表しています
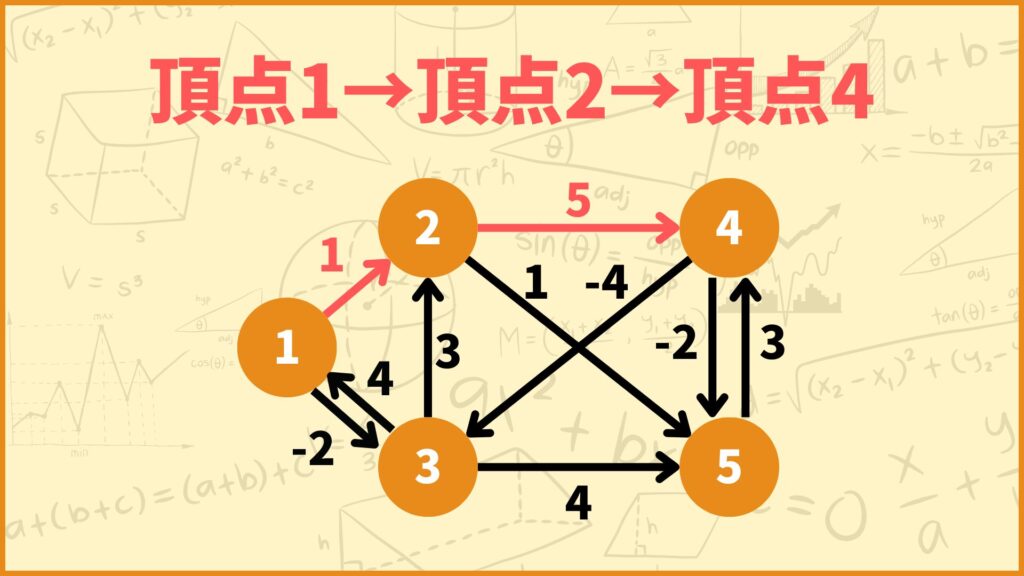
STEP 2で得られた行列の \((i,j)\) 成分は \(d_{ij}^{(2)}\) となっており、\(d_{ij}^{(2)}\) は頂点1と頂点2しか通れないときの \(i\)~\(j\) 間の最短距離を表しています。つまりこの行列は
「全ての2頂点間における、頂点1と頂点2しか通れないときの最短距離」
をまとめた行列となっているんです。
STEP 3
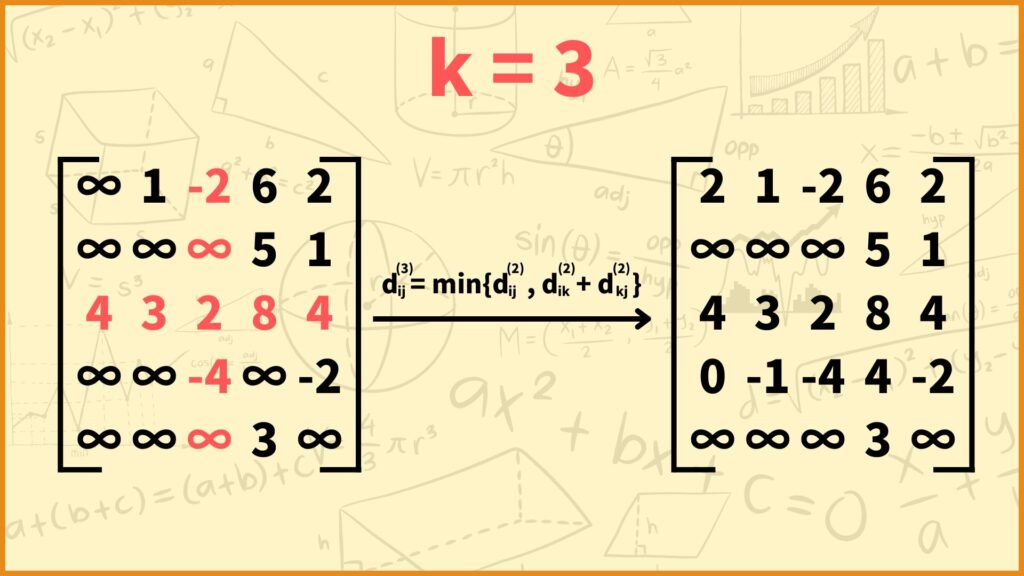
(上図の左側の行列の \((i,j)\) 成分は \(d_{ij}^{(2)}\) を表しており、右側の行列の \((i,j)\) 成分は \(d_{ij}^{(3)}\) を表しています。)
STEP 3では \(d_{ij}^{(3)}\)、つまり
「通って良い頂点が頂点1と頂点2と頂点3の場合における2頂点間の最短距離」
を求めていきます。下の式に従って \(d_{ij}^{(3)}\) の値を決めていけばOKです。
\(d_{ij}^{(3)} = \min\{d_{ij}^{(2)}, d_{i3}^{(2)} + d_{3j}^{(2)}\}\)
STEP 1とほぼ同じ操作を行うので、変化があった成分だけ説明します。
始点:頂点1
\(d_{11}^{(3)} = \min\{d_{11}^{(2)}, d_{13}^{(2)} + d_{31}^{(2)}\}=\min\{\infty, -2+4\}=2\)
始点:頂点4
\(d_{41}^{(3)} = \min\{d_{41}^{(2)}, d_{43}^{(2)} + d_{31}^{(2)}\}=\min\{\infty, -4+4\}=0\)
\(d_{42}^{(3)} = \min\{d_{42}^{(2)}, d_{43}^{(2)} + d_{32}^{(2)}\}=\min\{\infty, -4+3\}=-1\)
\(d_{44}^{(3)} = \min\{d_{44}^{(2)}, d_{43}^{(2)} + d_{34}^{(2)}\}=\min\{\infty, -4+8\}=4\)
例えば \((i,j) = (4,2)\) について考えてみましょう。STEP 2より
\(d_{42}^{(2)} = \infty\)
\(d_{43}^{(2)} = -4, d_{32}^{(2)} = 3\)
であることが分かっています。そのためさっきの式に従って \(d_{42}^{(3)}\) を計算すると
\(d_{42}^{(3)} = \min\{\infty, -4+3\} = -1\)
となります。これは途中で通っても良い頂点が頂点1と頂点2と頂点3のとき、頂点4~頂点2間の最短距離が-1であることを表しています。
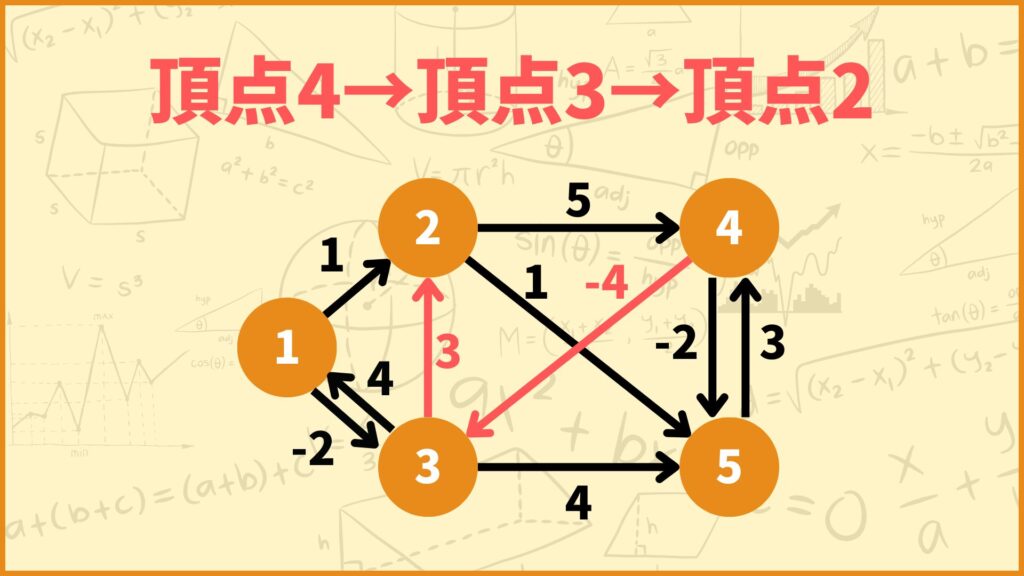
STEP 3で得られた行列の \((i,j)\) 成分は \(d_{ij}^{(3)}\) となっており、\(d_{ij}^{(3)}\) は頂点1と頂点2と頂点3しか通れないときの \(i\)~\(j\) 間の最短距離を表しています。つまりこの行列は
「全ての2頂点間における、頂点1と頂点2と頂点3しか通れないときの最短距離」
をまとめた行列となっているんです。
STEP 4
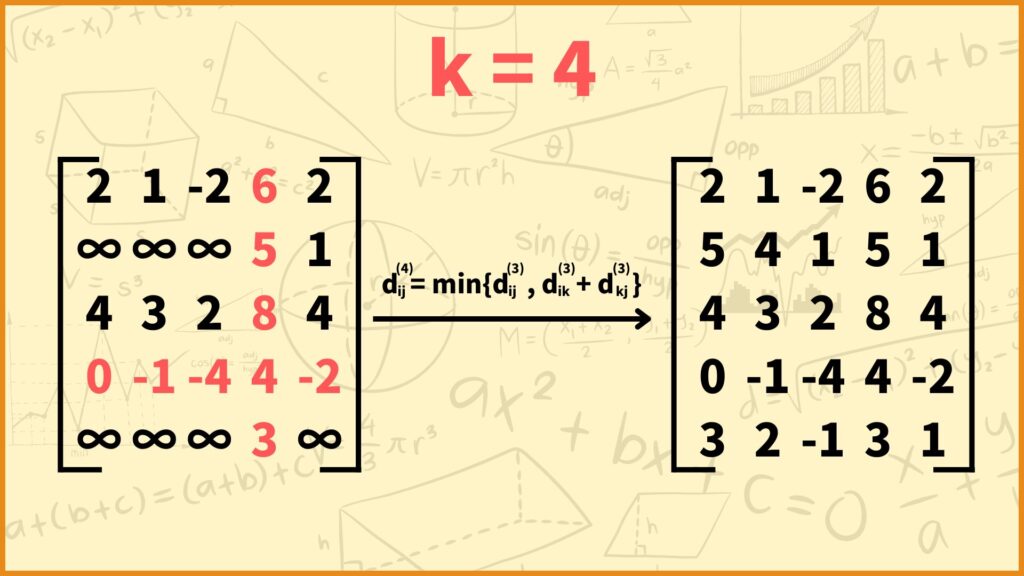
(上図の左側の行列の \((i,j)\) 成分は \(d_{ij}^{(3)}\) を表しており、右側の行列の \((i,j)\) 成分は \(d_{ij}^{(4)}\) を表しています。)
STEP 4では \(d_{ij}^{(4)}\)、つまり
「通って良い頂点が頂点1と頂点2と頂点3と頂点4の場合における2頂点間の最短距離」
を求めていきます。結論以下の式に従って \(d_{ij}^{(4)}\) の値を決めていけばOKです。
\(d_{ij}^{(4)} = \min\{d_{ij}^{(3)}, d_{i4}^{(3)} + d_{4j}^{(3)}\}\)
STEP 1とほぼ同じ操作を行うので、変化があった成分だけ説明します。
始点:頂点2
\(d_{21}^{(4)} = \min\{d_{21}^{(3)}, d_{24}^{(3)} + d_{41}^{(3)}\}=\min\{\infty, 5+0\}=5\)
\(d_{22}^{(4)} = \min\{d_{22}^{(3)}, d_{24}^{(3)} + d_{42}^{(3)}\}=\min\{\infty, 5-1\}=4\)
\(d_{23}^{(4)} = \min\{d_{23}^{(3)}, d_{24}^{(3)} + d_{43}^{(3)}\}=\min\{\infty, 5-4\}=1\)
始点:頂点5
\(d_{51}^{(4)} = \min\{d_{51}^{(3)}, d_{54}^{(3)} + d_{41}^{(3)}\}=\min\{\infty, 3+0\}=3\)
\(d_{52}^{(4)} = \min\{d_{52}^{(3)}, d_{54}^{(3)} + d_{42}^{(3)}\}=\min\{\infty, 3-1\}=2\)
\(d_{53}^{(4)} = \min\{d_{53}^{(3)}, d_{54}^{(3)} + d_{43}^{(3)}\}=\min\{\infty, 3-4\}=-1\)
\(d_{55}^{(4)} = \min\{d_{55}^{(3)}, d_{54}^{(3)} + d_{45}^{(3)}\}=\min\{\infty, 3-2\}=1\)
例えば \((i,j) = (5,1)\) について考えてみましょう。STEP 3より
\(d_{51}^{(3)} = \infty\)
\(d_{54}^{(3)} = 3, d_{41}^{(3)} = 0\)
であることが分かっています。そのためさっきの式に従って \(d_{51}^{(4)}\) を計算すると
\(d_{51}^{(4)} = \min\{\infty, 3+0\} = 3\)
となります。これは途中で通っても良い頂点が頂点1と頂点2と頂点3と頂点4のとき、頂点5~頂点1間の最短距離が3であることを表しています。
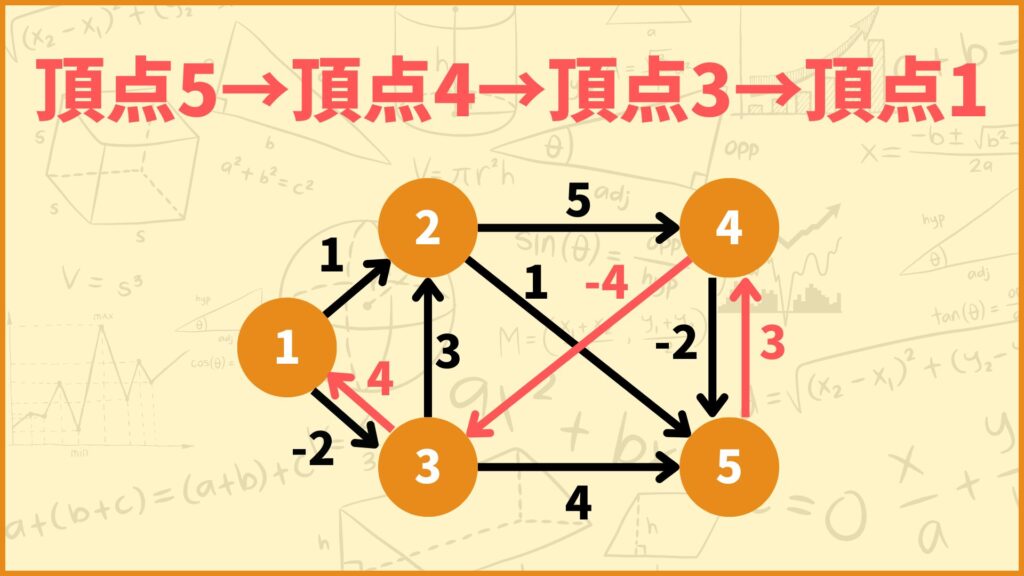
STEP 4で得られた行列の \((i,j)\) 成分は \(d_{ij}^{(4)}\) となっており、\(d_{ij}^{(4)}\) は頂点1と頂点2と頂点3と頂点4しか通れないときの \(i\)~\(j\) 間の最短距離を表しています。つまりこの行列は
「全ての2頂点間における、頂点1と頂点2と頂点3と頂点4しか通れないときの最短距離」
をまとめた行列となっているんです。
STEP 5
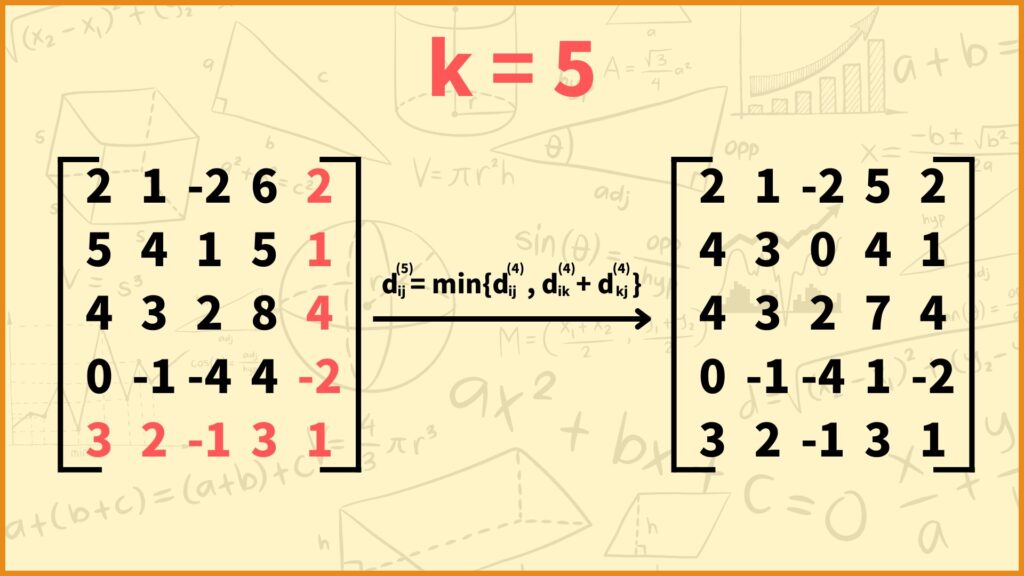
(上図の左側の行列の \((i,j)\) 成分は \(d_{ij}^{(2)}\) を表しており、右側の行列の \((i,j)\) 成分は \(d_{ij}^{(3)}\) を表しています。)
STEP 5では \(d_{ij}^{(5)}\)、つまり
「通って良い頂点が頂点1と頂点2と頂点3と頂点4と頂点5の場合における2頂点間の最短距離」
を求めていきます。下の式に従って \(d_{ij}^{(5)}\) の値を決めていけばOKです。
\(d_{ij}^{(5)} = \min\{d_{ij}^{(4)}, d_{i5}^{(4)} + d_{5j}^{(4)}\}\)
STEP 1とほぼ同じ操作を行うので、変化があった成分だけ説明します。
始点:頂点1
\(d_{14}^{(5)} = \min\{d_{14}^{(4)}, d_{15}^{(4)} + d_{54}^{(4)}\}=\min\{6, 2+3\}=5\)
始点:頂点2
\(d_{21}^{(5)} = \min\{d_{21}^{(4)}, d_{25}^{(4)} + d_{51}^{(4)}\}=\min\{5, 1+3\}=4\)
\(d_{22}^{(5)} = \min\{d_{22}^{(4)}, d_{25}^{(4)} + d_{52}^{(4)}\}=\min\{5, 1+2\}=3\)
\(d_{23}^{(5)} = \min\{d_{23}^{(4)}, d_{25}^{(4)} + d_{53}^{(4)}\}=\min\{5, 1-1\}=0\)
\(d_{24}^{(5)} = \min\{d_{24}^{(4)}, d_{25}^{(4)} + d_{54}^{(4)}\}=\min\{5, 1+3\}=4\)
始点:頂点3
\(d_{34}^{(5)} = \min\{d_{34}^{(4)}, d_{35}^{(4)} + d_{54}^{(4)}\}=\min\{8, 4+3\}=7\)
始点:頂点4
\(d_{44}^{(5)} = \min\{d_{44}^{(4)}, d_{45}^{(4)} + d_{54}^{(4)}\}=\min\{4, -2+3\}=1\)
例えば \((i,j) = (2,1)\) について考えてみましょう。STEP 4より
\(d_{21}^{(4)} = 5\)
\(d_{25}^{(4)} = 1, d_{51}^{(1)} = 3\)
であることが分かっています。そのためさっきの式に従って \(d_{21}^{(4)}\) を計算すると
\(d_{25}^{(5)} = \min\{5, 1+3\} = 4\)
となります。これは途中で通っても良い頂点が頂点1と頂点2と頂点3と頂点4と頂点5のとき、頂点2~頂点1間の最短距離が3であることを表しています。
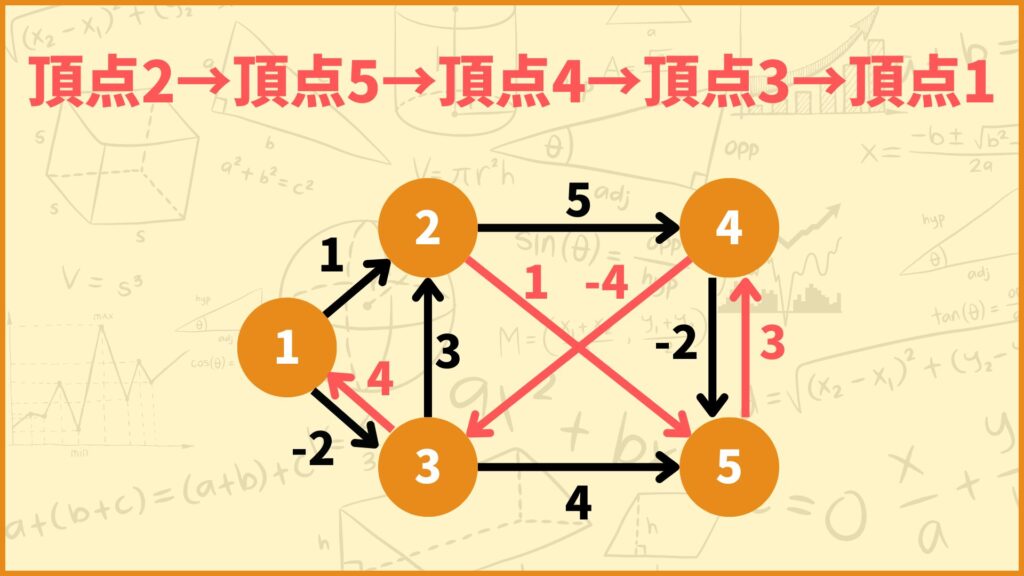
STEP 5で得られた行列の \((i,j)\) 成分は \(d_{ij}^{(5)}\) となっており、\(d_{ij}^{(5)}\) は頂点1と頂点2と頂点3と頂点4と頂点5しか通れないときの \(i\)~\(j\) 間の最短距離を表しています。
これってつまり全ての頂点を通って良いってことですよね。すなわちこの行列は
「全ての2頂点間における最短距離」
をまとめた行列となり、今回求めたいものとなります。
ワーシャルフロイド法を終了する
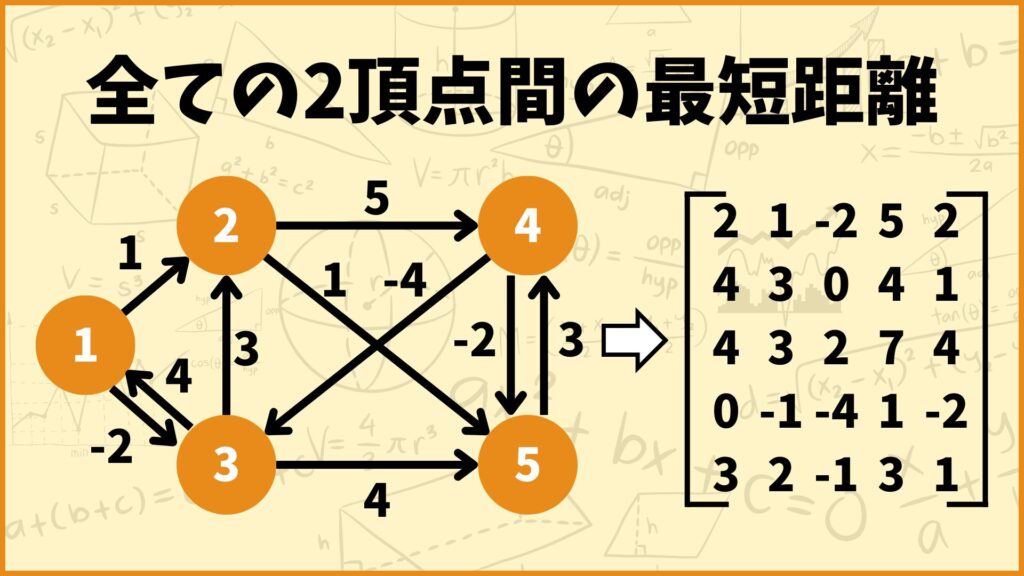
今回のグラフは頂点数が5個なので、5回のステップでワーシャルフロイド法が終了します。ということでSTEP 5で得られた行列が全ての2頂点間の最短距離を表すグラフとなっています。
例えば頂点2~頂点1間の最短距離は行列の \((2,1)\) 成分なので3となります。
ワーシャルフロイド法に関する豆知識
最後にワーシャルフロイド法に関する豆知識を紹介していきます。
負の重みの辺があってもOK

ワーシャルフロイド法は負の重みを持つ辺があるグラフでも使えるアルゴリズムです。具体例で用いた上のグラフにも負の重みを持つ辺がありますね。
最短経路問題でよく用いられるアルゴリズムにダイクストラ法がありますが、こちらは辺の重みが非負でないと使えません。
\\\ ダイクストラ法はこちらの記事で解説しています! ///
負閉路を検知できる
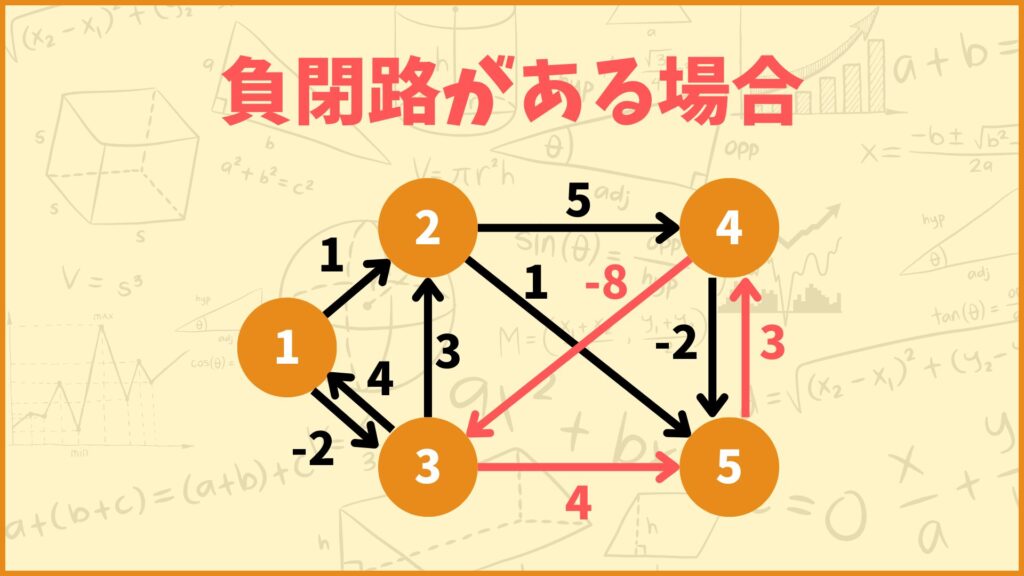
上図の赤い閉路は辺の重みの合計が-1で負の値となりますね。このような閉路のことを負閉路と呼びます。負閉路があるグラフだと、負閉路を周回すれば無限に重みの合計を小さくすることができてしまいます。
でもワーシャルフロイド法は負閉路を検知することができます。結論ワーシャルフロイド法で得られた行列の対角成分の値に負の値があったら負閉路があります。
ワーシャルフロイド法で得られた行列の \((i,i)\) 成分が負の値だったとします。\((i,i)\) 成分の値は頂点 \(i\) から頂点 \(i\) への最短距離、つまり頂点 \(i\) を含むある閉路の重みを表しています。これが負ということは、頂点 \(i\) を含む負閉路が存在することを表しています。
\\\ ワーシャルフロイド法と負閉路についてはこちらの記事で解説しています! ///
計算量は\(O(n^3)\)
グラフの頂点数を\(n\)とするとワーシャルフロイド法の計算量は\(O(n^3)\)です。イメージとしては
\(k\)の反復に\(O(n)\)回
\(i\)の反復に\(O(n)\)回
\(j\)の反復に\(O(n)\)回
\(d_{ij}^{(k)}\)の計算時間が\(O(1)\)
つまり計算時間が\(O(1)\)の計算を\(O(n^3)\)回行うので計算量が\(O(n^3)\)となります。
少しマニアックな話になりますが、全ての2頂点間の最短経路を求める問題はベルマンフォード法を使っても解けるんです。ベルマンフォード法は2頂点が与えられたときに計算量\(O(mn)\)(\(m\):グラフの辺数、\(n\):グラフの頂点数)でその2頂点間の最短距離を求められるアルゴリズムなんですが、全ての2頂点に対してベルマンフォード法を適用すれば全ての2頂点間の最短経路を求めることができます。でも2頂点の選び方の総数が\(O(n^2)\)通りあるのでベルマンフォード法で全ての2頂点間の最短距離を求めようとすると計算量が\(O(mn^3)\)となります。
これに比べてワーシャルフロイド法は\(O(n^3)\)で全ての2頂点間の最短距離を求めることができるのでこっちの方が高速なんです。
おわりに
いかがでしたか。
今回の記事ではワーシャルフロイド法について解説していきました。
今後もこのような組合せ最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。