- ハンガリー法（ハンガリアンアルゴリズム）ってなに？
- ハンガリー法の手順ってなに？
- ハンガリー法を使って割当問題を解きたい…
こんにちは！しゅんです！
今回の記事ではハンガリー法（ハンガリアンアルゴリズム）ついて解説していきます！
前回の記事で割当問題を整数計画問題として定式化する方法を解説しました。この記事ではちょっと視点を変えて、割当問題をハンガリー法で解くやり方を１つずつ丁寧に説明したいと思います！
それではやっていきましょう！
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください！
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます！
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学（けいえいこうがく、英: engineering management）は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
ハンガリー法の手順を1つずつ説明する
説明で使用する2つの具体例
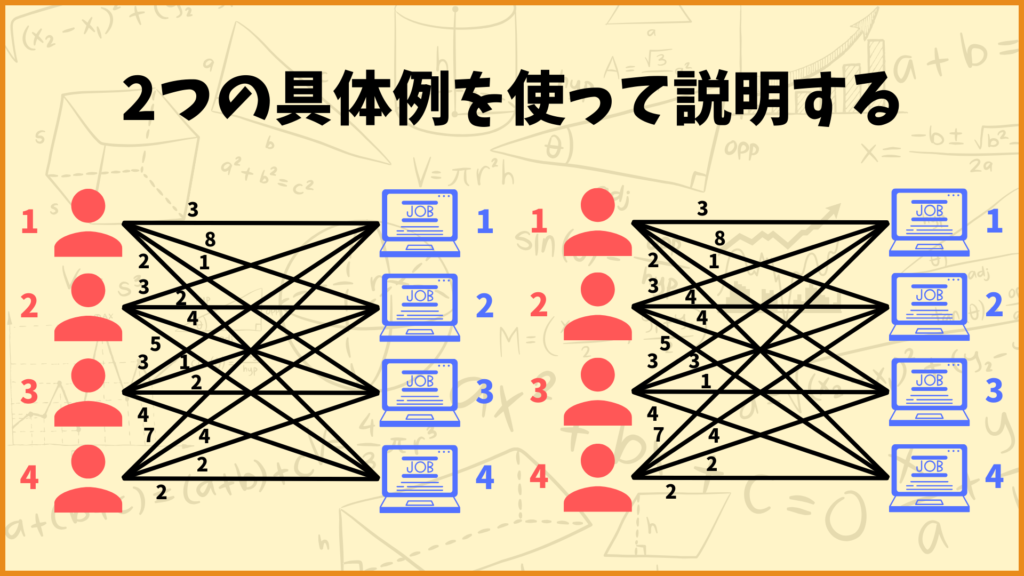
今回は上の2つの具体例を使ってハンガリー法を説明したいと思います。
事前準備
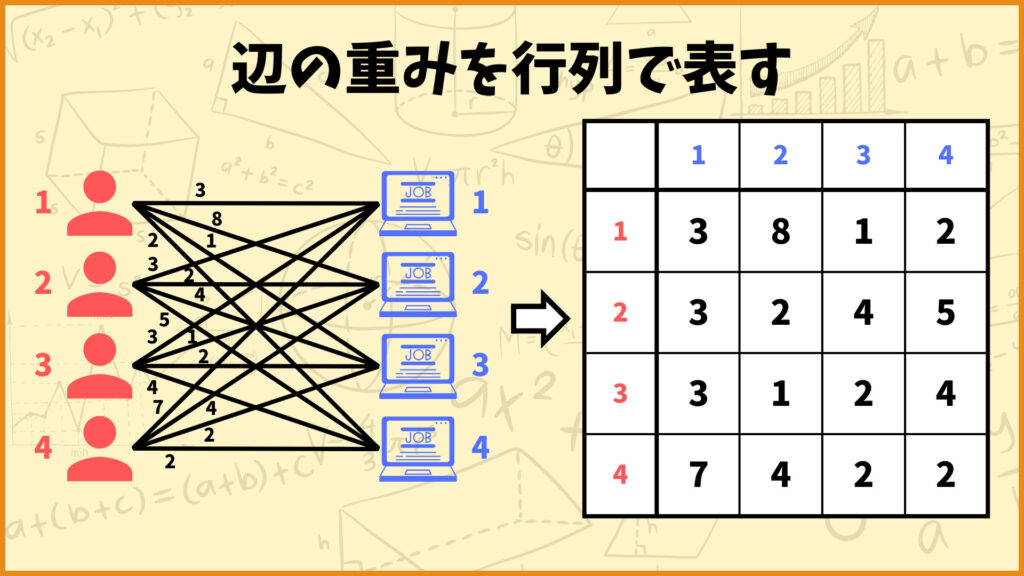
ハンガリー法を説明するための事前準備として辺の重みを行列で表します。各行が各従業員、各列が各仕事、\((i,j)\)成分が辺\((i,j)\)の重みとなるような行列を作りましょう。例えば上図の例で言うと従業員1と仕事2を結ぶ辺の重みが8なので、\((1,2)\)成分の値を8にします。
この行列を使ってハンガリー法の説明をしたいと思います。
ハンガリー法の手順
STEP. 1 :
各行に対して、その行の成分からその行の成分の最小値を引く。
STEP. 2 :
各列に対して、その列の成分からその列の成分の最小値を引く。
STEP. 3 :
値が0となる成分の辺だけから作られた2部グラフで完全マッチングが作れるかを調べる。
作れる → 終了
作れない → STEP. 4へ
STEP. 4 :
全ての0の成分をカバーするような縦線・横線を引く。このとき線の本数が最小なものを考える。
STEP. 5 :
線でカバーされていない成分からそれら成分の最小値を引く。
またその最小値を、縦線・横線両方でカバーされている成分に足す。
STEP. 3に戻る。
なんか長くてややこしそうに見えるので1つずつ丁寧に解説していきます。
具体例1を使って説明をする
事前準備
まず最初に辺の重みを行列で表しましょう。
STEP. 1の説明
STEP. 1でやることは
「各行に対して、その行の成分からその行の成分の最小値を引く。」
です。例えば1行目の各成分を見ていきましょう。1行目の成分は1列目から順に\(3,8,1,2\)となっています。これらの数字で最も値が小さいのは\((1,3)\)成分の\(1\)なので各成分から1を引きましょう。
\(3-1 = 2\)
\(8-1 = 7\)
\(1-1 = 0\)
\(2-1 = 1\)
2～4行目に対しても同じ操作を行います。2,3,4行目の各成分の中でもっとも小さいのはそれぞれ2,1,2なのでこれらを引きましょう。
そうすると上図の右側の行列が得られると思います。
STEP. 2の説明
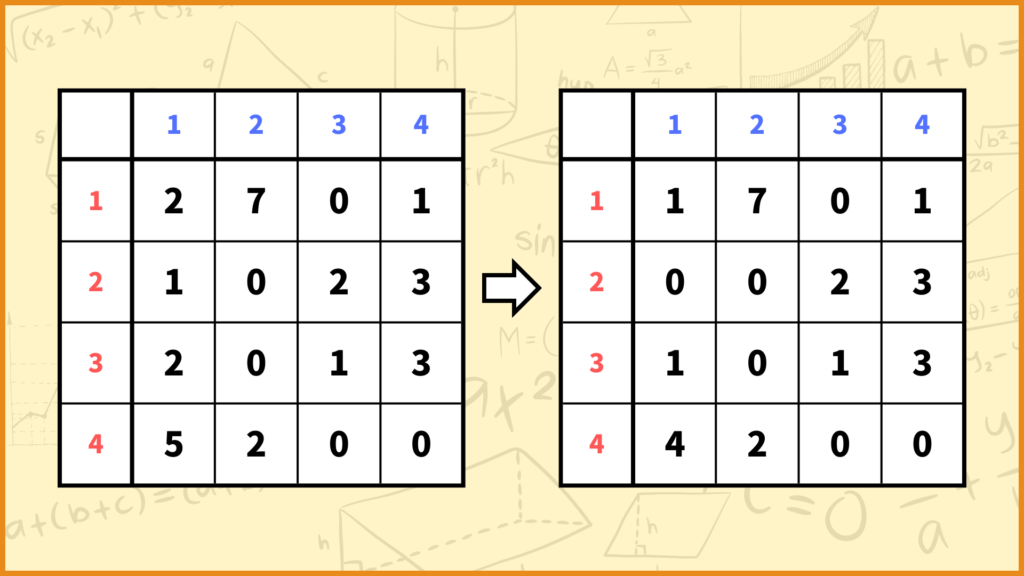
STEP. 2でやることは
「各列に対して、その列の成分からその列の成分の最小値を引く。」
です。例えば1列目の各成分を見ていきましょう。1列目の成分は1行目から順に\(2,1,2,5\)となっています。これらの数字で最も値が小さいのは\((2,1)\)成分の1なので各成分から1を引きましょう。
\(2-1 = 1\)
\(1-1 = 0\)
\(2-1 = 1\)
\(5-1 = 4\)
2～4列目に対しても同じ操作を行います。2,3,4列目の各成分の中でもっとも小さいのは全て0なのでそれぞれ0を引きましょう。（つまりそのままってことです。）
そうすると上図の右側の行列が得られると思います。
STEP. 3の説明
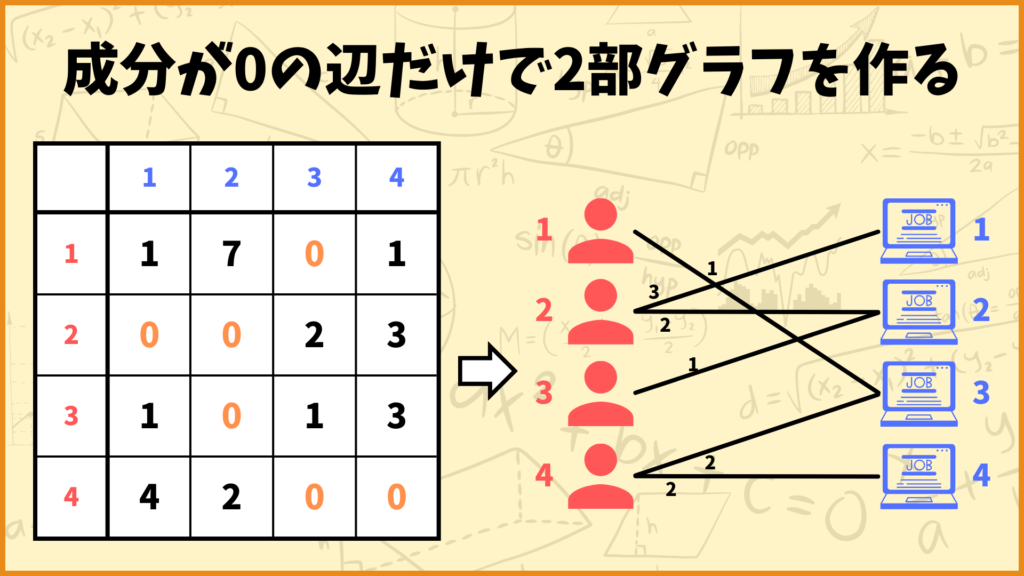
STEP. 3でやることは
「値が0となる成分の辺だけから作られた2部グラフで完全マッチングが作れるかを調べる。」
です。ということでまず値が0となる成分の辺だけから作られた2部グラフを作ってみました。値が0の成分は
\((1,3),(2,1),(2,2),(3,2),(4,3),(4,4)\)
なのでそれに対応する辺だけを使いましょう。
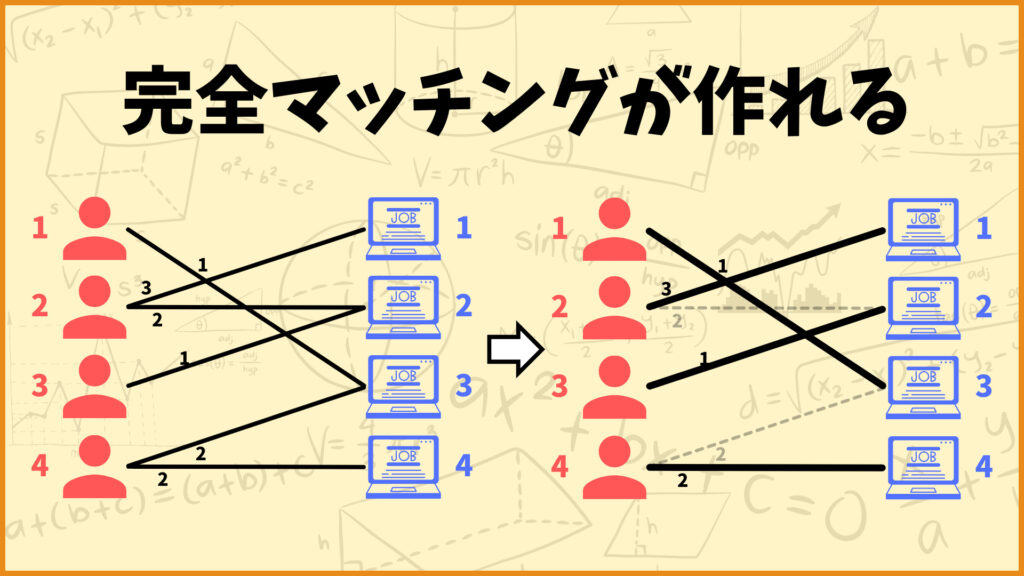
この2部グラフに完全マッチングが存在するかを考えましょう。今回の場合は辺\((1,3),(2,1),(3,2),(4,4)\)を選ぶことで完全マッチングが得られます。
実はここで得られた完全マッチングが元の2部グラフの最小重み完全マッチングになっているんです。
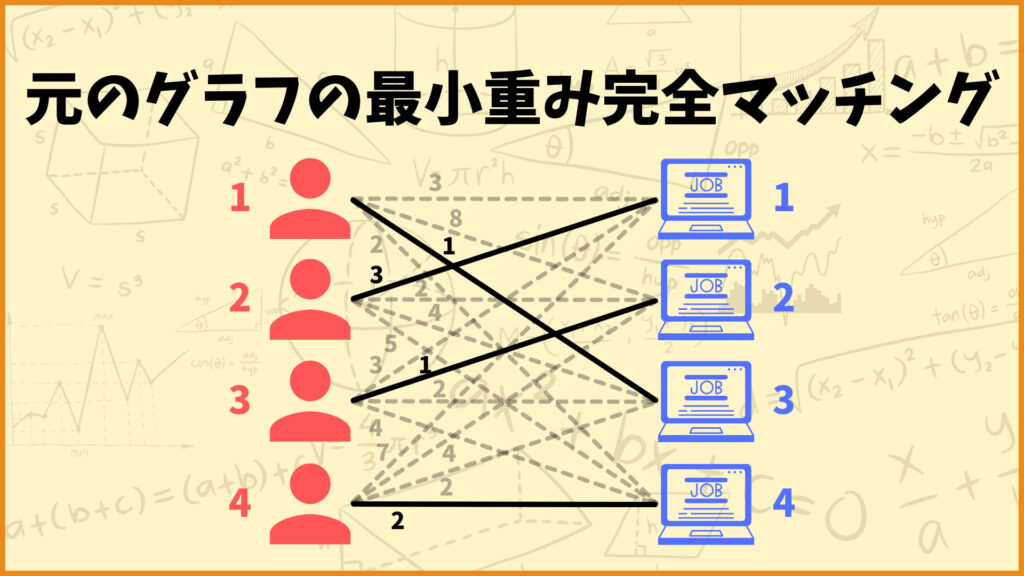
元のグラフの最小重み完全マッチングも辺\((1,3),(2,1),(3,2),(4,4)\)となります。ということでこの時点でハンガリー法が終了します。
ちなみにこのSTEP. 3の操作はわざわざグラフを作らなくても、行列上でできてしまいます。
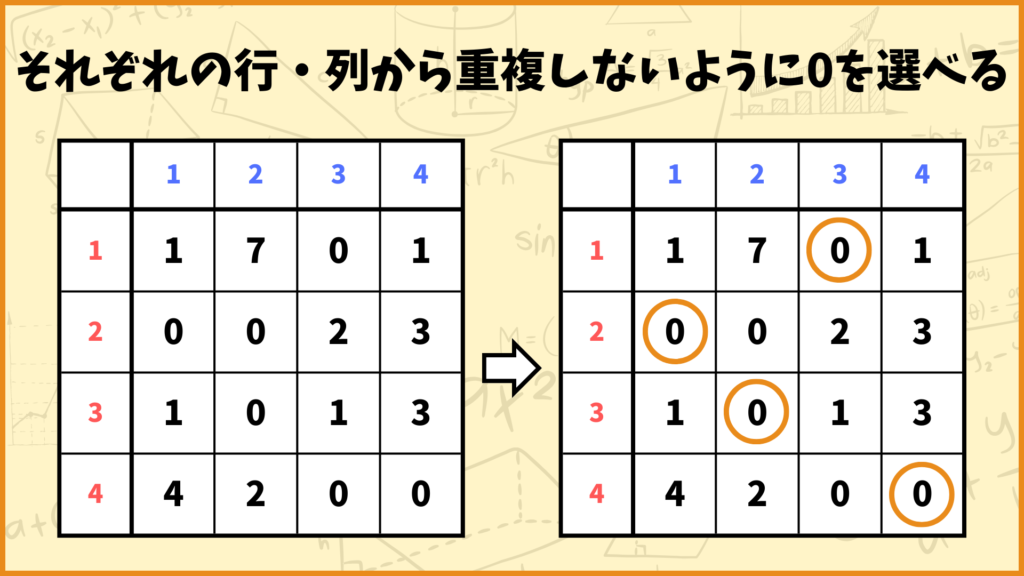
完全マッチングが作れるかどうかを調べることは、行列上で各行・列から重複しないように0を選べるかどうかを調べることと同じです。今回の例だと上図のように0を選ぶことができるので、操作を終了します。
具体例2を使って説明をする
事前準備
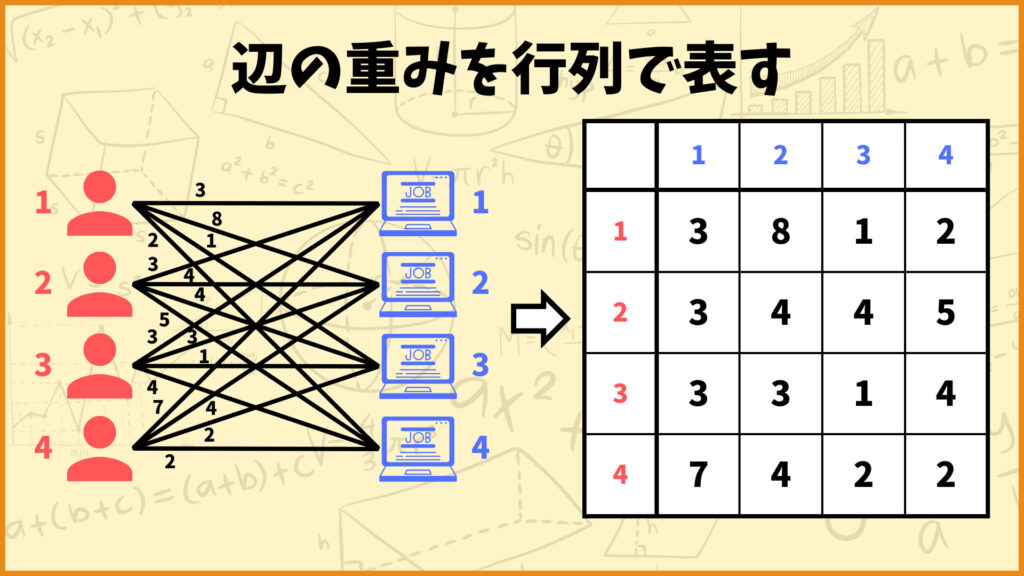
まず最初に辺の重みを行列で表しましょう。
STEP. 1の説明
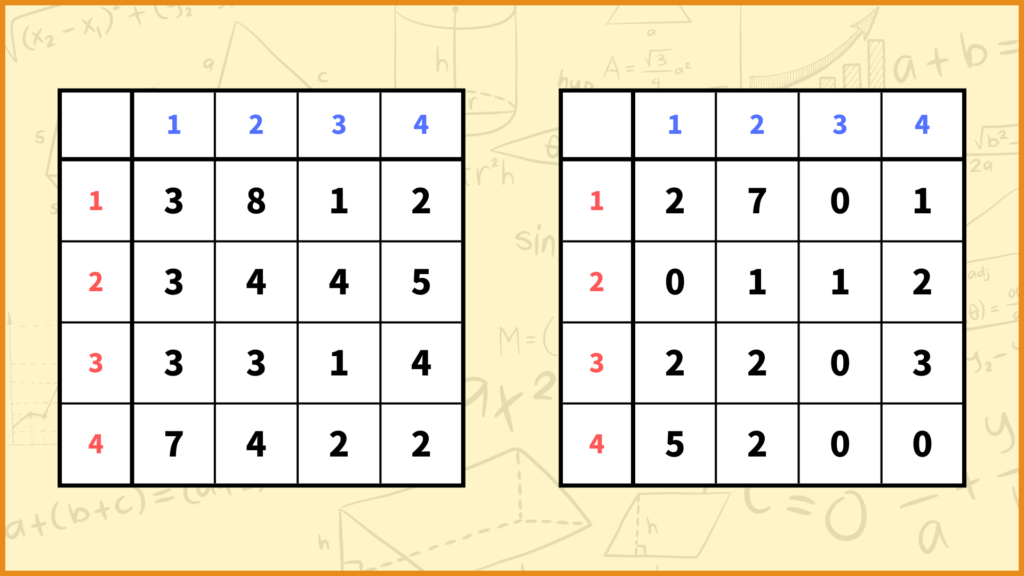
STEP. 1でやることは
「各行に対して、その行の成分からその行の成分の最小値を引く。」
です。例えば1行目の各成分を見ていきましょう。1行目の成分は1列目から順に\(3,8,1,2\)となっています。これらの数字で最も値が小さいのは\((1,3)\)成分の1なので各成分から1を引きましょう。
\(3-1 = 2\)
\(8-1 = 7\)
\(1-1 = 0\)
\(2-1 = 1\)
2～4行目に対しても同じ操作を行います。2,3,4行目の各成分の中でもっとも小さいのはそれぞれ3,1,2なのでこれらを引き算しましょう。
そうすると上図の右側の行列が得られると思います。
STEP. 2の説明
STEP. 2でやることは
「各列に対して、その列の成分からその列の成分の最小値を引く。」
です。例えば2列目の各成分を見ていきましょう。2列目の成分は1行目から順に\(7,1,2,2\)となっています。これらの数字で最も値が小さいのは\((2,2)\)成分の1なので各成分から1を引きましょう。
\(7-1 = 6\)
\(1-1 = 0\)
\(2-1 = 1\)
\(2-1 = 1\)
1,3,4列目に対しても同じ操作を行います。1,3,4列目の各成分の中でもっとも小さいのは全て0なのでそれぞれ0を引き算しましょう。（つまりそのままってことです。）
そうすると上図の右側の行列が得られると思います。
STEP. 3の説明
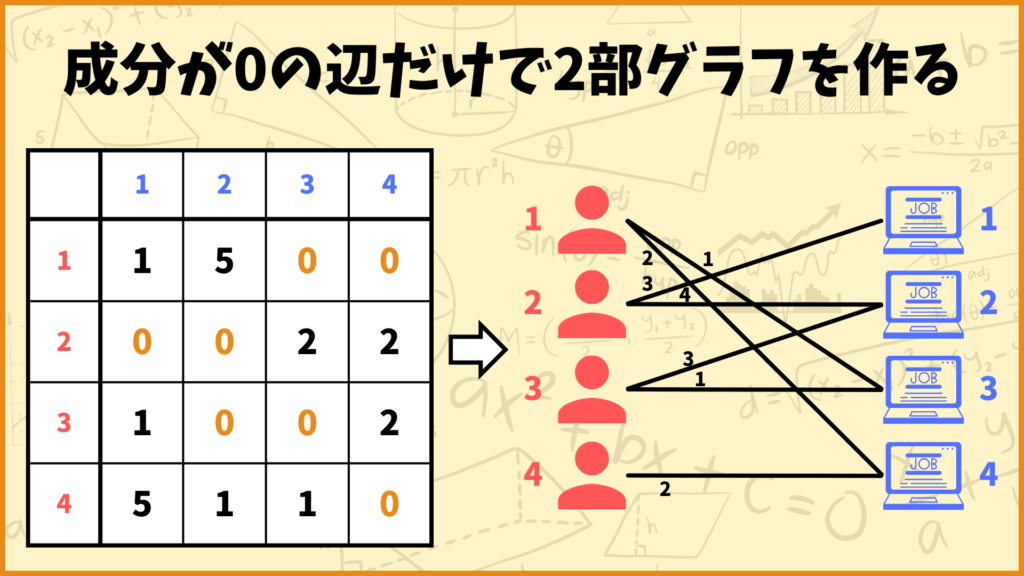
STEP. 3でやることは
「値が0となる成分の辺だけから作られた2部グラフで完全マッチングが作れるかを調べる。」
です。ということでまず値が0となる成分の辺だけから作られた2部グラフを作ってみました。値が0の成分は
\((1,3),(2,1),(2,2),(3,3),(4,3),(4,4)\)
なのでそれに対応する辺だけを使いましょう。残念ながらこのグラフには完全マッチングが存在しません。そのためSTEP. 4に進みます。
STEP. 4の説明
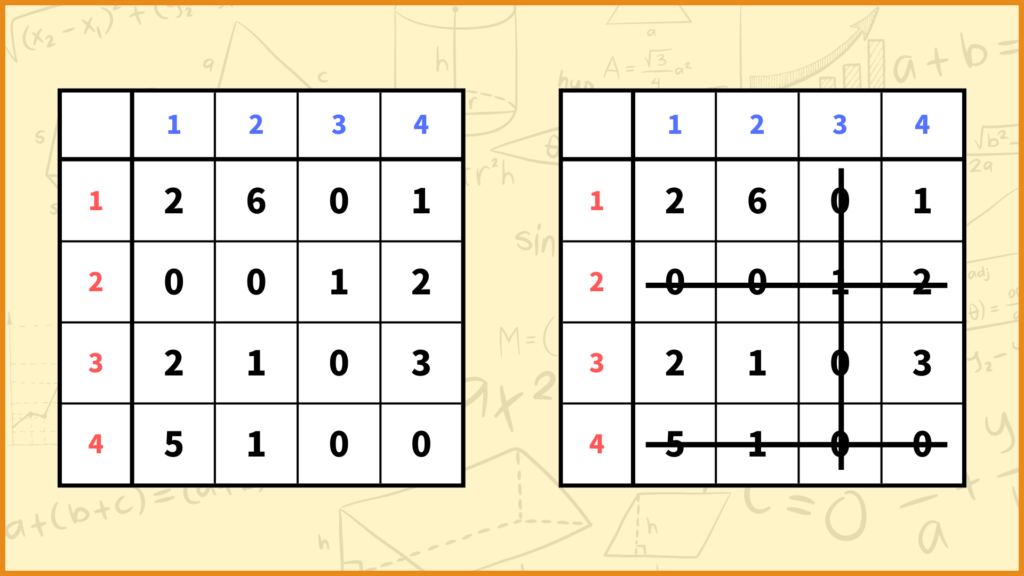
STEP. 4でやることは
「全ての0の成分をカバーするような縦線・横線を引く。このとき線の本数が最小なものを考える。」
です。今回は上図のように線を引くことで全ての0の成分をカバーできます。（上図の例ではどう頑張っても2本の線で全ての0の成分をカバーすることはできません。）
STEP. 5の説明
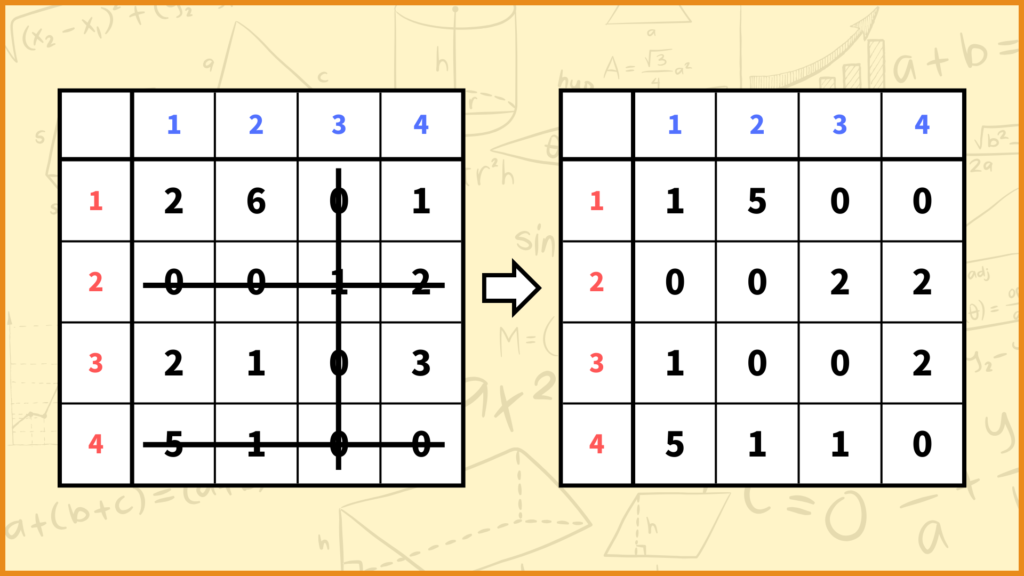
STEP. 5でやることは
「線でカバーされていない成分からそれら成分の最小値を引く。」
「またその最小値を、縦線・横線両方でカバーされている成分に足す。」
です。線でカバーされていない成分は左上から順番に\((1,1),(1,2),(1,4),(3,1),(3,2),(3,4)\)です。この中で最も値が小さいのは\((1,4),(3,2)\)成分の1なので、これらの成分から1を引きましょう。
さらに縦線・横線両方でカバーされている成分は\((2,3),(3,3)\)なのでこの成分に1を足しましょう。そうすると上図の右側の行列が得られると思います。
STEP. 5の操作が全て終了したのでSTEP. 3に戻りましょう。
STEP. 3に戻る
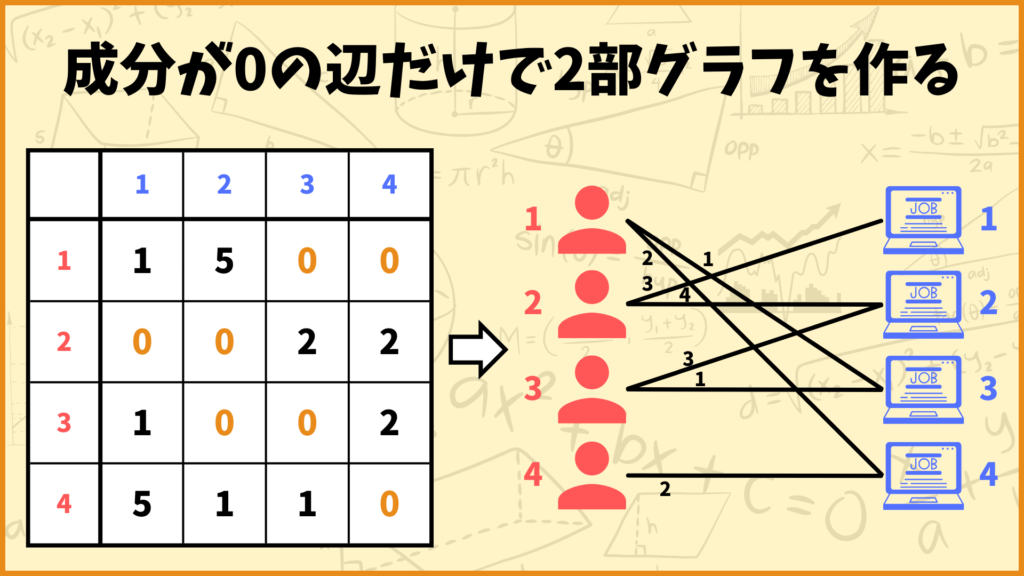
STEP. 3に戻ります。STEP. 3でやることは
「値が0となる成分の辺だけから作られた2部グラフで完全マッチングが作れるかを調べる。」
です。ということで値が0となる成分の辺だけから作られた2部グラフを作ってみました。値が0の成分は
\((1,3),(1,4),(2,1),(2,2),(3,2),(3,3),(4,4)\)
なのでそれに対応する辺だけを使いましょう。
この2部グラフに完全マッチングが存在するかを考えましょう。今回の場合は辺\((1,3),(2,1),(3,2),(4,4)\)を選ぶことで完全マッチングが得られます。
ここで得られた完全マッチングが元の2部グラフの最小重み完全マッチングになっています。
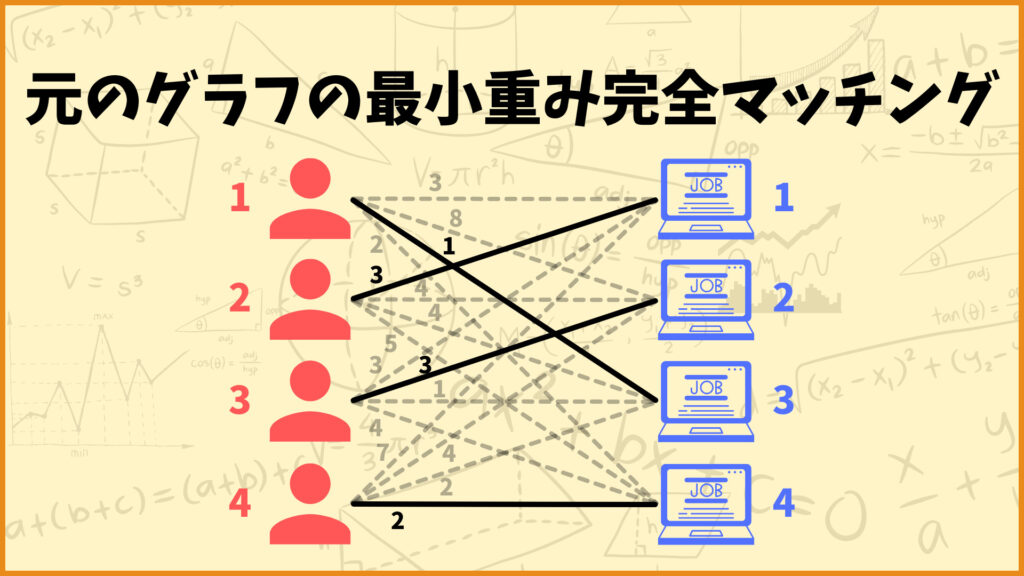
元のグラフの最小重み完全マッチングも辺\((1,3),(2,1),(3,2),(4,4)\)となります。ということでこの時点でハンガリー法が終了します。
今回はハンガリー法の手順について紹介しました。下の記事ではどうしてハンガリー法で割当問題の最適解が得られるのかについて考えています！
おわりに
いかがでしたか。
今回の記事ではハンガリー法について解説していきました。
今後もこのような組合せ最適化に関する記事を書いていきます！
最後までこの記事を読んでくれてありがとうございました。
