- ロジスティック回帰ってなに?
- ロジスティック回帰のアルゴリズムが知りたい…
- ロジスティック回帰を数式で理解したい…
こんにちは!しゅんです!
今回はロジスティック回帰分析について解説していきます!
この記事はロジスティック回帰のアルゴリズムの解説をして、次回の記事ではロジスティック回帰をpythonで実装する方法を解説します。
それではやっていきましょう!
本記事を書くにあたって、この書籍を使って勉強しました。
ロジスティック回帰ってなに?
ロジスティック回帰:
データが2つのグループのどっちに属すかを確率で表す手法
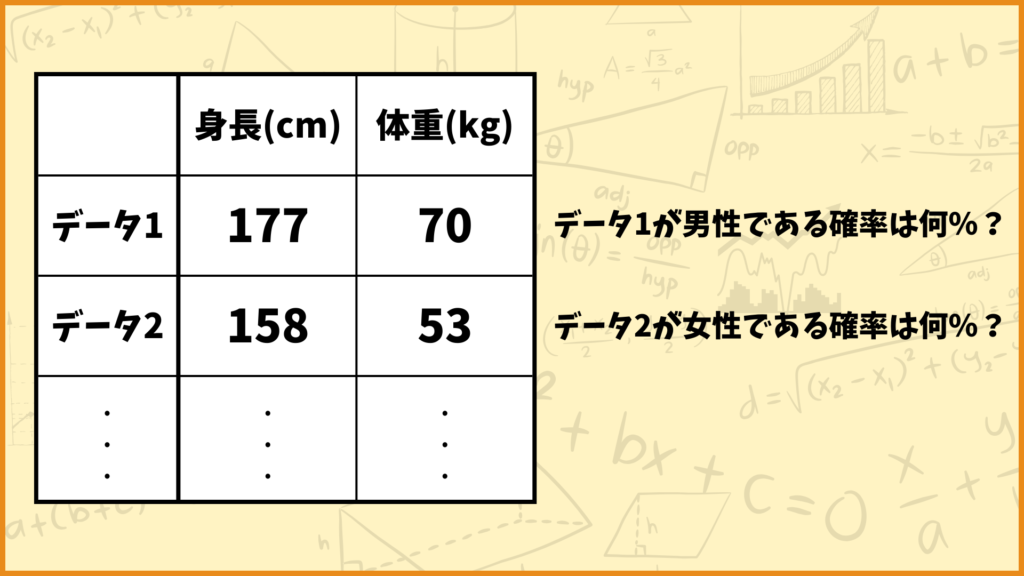
上図の例を見てみましょう。例えばデータ1は身長177cm、体重70kgというデータですが、これは男性のデータっぽいですね。一方でデータ2は身長158cm、体重53kgのデータですが、これは女性のデータっぽいですね。
ロジスティック回帰では与えられたデータがどれだけ男性っぽいか、どれだけ女性っぽいかを確率として出力します。データ1を入力したら90%という数字が出力されてデータ2を入力したら15%が出力されるようなイメージです。
ロジスティック回帰による予測結果はそのデータが男性である確率を表します。女性である確率は1から男性である確率を引き算すれば計算できます。今の例で言うとデータ1が女性である確率は10%、データ2が女性である確率は85%と計算できます。
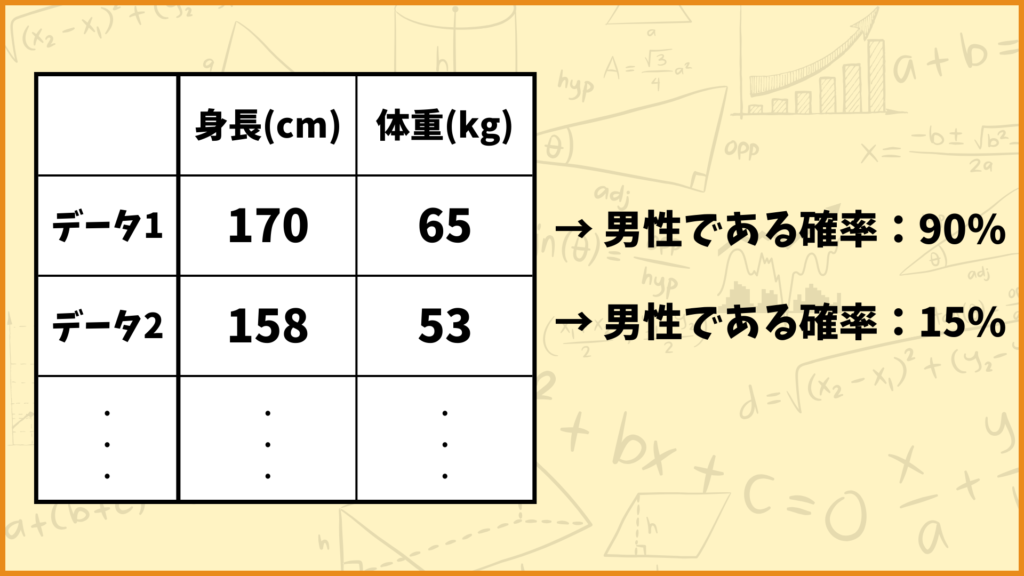
ロジスティック回帰は教師あり学習の1つです。すなわちそのデータが男性なのか女性なのかという正解のデータがある状態で学習を行います。
ロジスティック回帰の説明に使うデータ
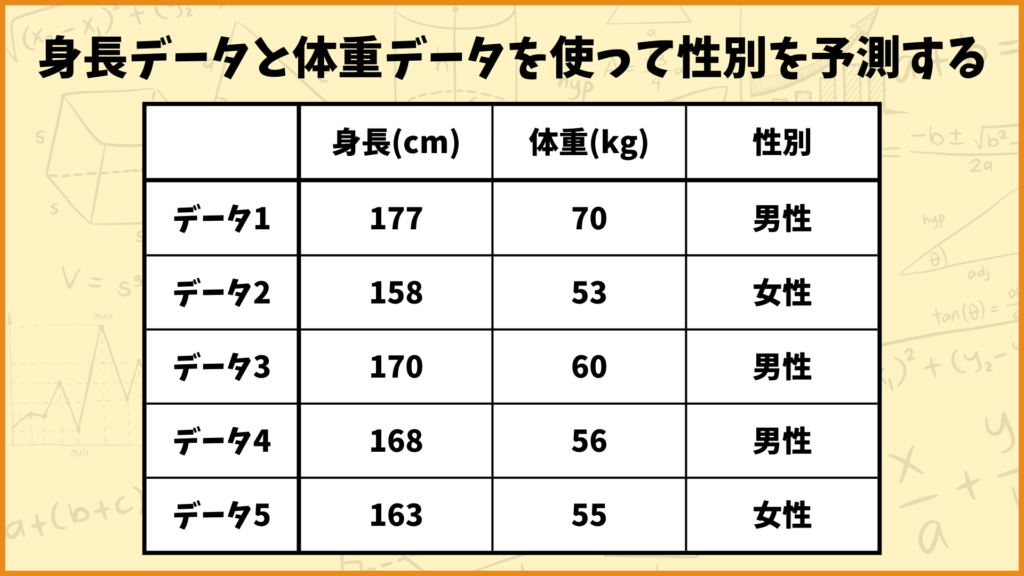
今回は上のデータを使ってロジスティック回帰のアルゴリズムを説明したいと思います。上のデータは
説明変数:身長、体重
目的変数:性別
となっています。すなわち身長、体重のデータを使って性別を予測します。
数式を使ってロジスティック回帰のアルゴリズムを説明する
ここからは実際にロジスティック回帰のアルゴリズムを説明していきます。ゴリゴリに数式を使うので1つずつ丁寧に解説していきます。なお第3章で説明したデータを使って説明します。
説明に使う文字を設定する
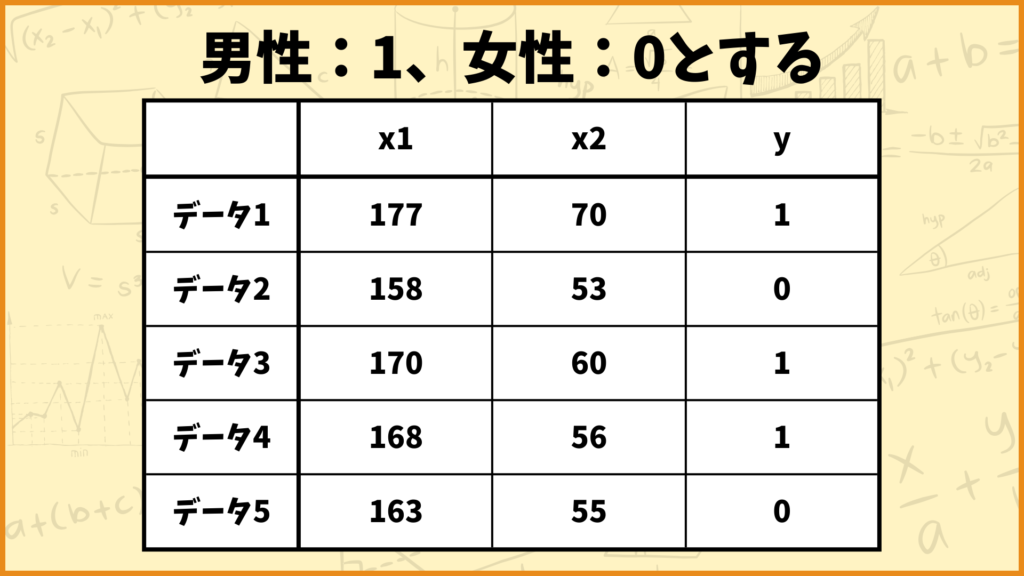
それではまずアルゴリズムの説明をするために文字を設定します。
身長データ:\(x_1\)
体重データ:\(x_2\)
性別データ:\(y\)
としました。なお性別データ\(y\)は男性なら1、女性なら0を取ります。またデータ \(i\) の身長データ \((x_1)\) は \(x_{i1}\) と表し、データ \(i\) の体重データ \((x_2)\) は \(x_{i2}\) と表します。各データは
\((x_{11},x_{12},y_1)=(177,70,1)\)
\((x_{21},x_{22},y_2)=(158,53,0)\)
\((x_{31},x_{32},y_3)=(170,60,1)\)
\((x_{41},x_{42},y_4)=(168,56,1)\)
\((x_{51},x_{52},y_5)=(163,55,0)\)
となっています。またパラメータとして\(a_0,a_1,a_2\)を用意します。
これらパラメータは後で登場するのでそのときに詳しく説明しますが、ロジスティック回帰ではこの\(a_0,a_1,a_2\)を動かして最適なパラメータを決定します。
重み付き和を計算する
それでは次に各データの重み付き和\(z_i\)を計算します。具体的には
\(z_1 = a_0+a_1x_{11}+a_2x_{12}\)
\(z_2 = a_0+a_1x_{21}+a_2x_{22}\)
\(z_3 = a_0+a_1x_{31}+a_2x_{32}\)
\(z_4 = a_0+a_1x_{41}+a_2x_{42}\)
\(z_5 = a_0+a_1x_{51}+a_2x_{52}\)
を計算します。例えば\((a_0,a_1,a_2)=(0,0.02,-0.04)\)としたときの各重み付き和の値は
\(z_1 = 0+0.02\times177-0.04\times70=0.74\)
\(z_2 = 0+0.02\times158-0.04\times53=1.04\)
\(z_3 = 0+0.02\times170-0.04\times60=1\)
\(z_4 = 0+0.02\times168-0.04\times56=1.12\)
\(z_5 = 0+0.02\times163-0.04\times55=1.06\)
と計算できます。この計算はパーセプトロンの重み付き和を計算するのと同じですね。
\\\ パーセプトロンの詳しい解説はこちらから! ///
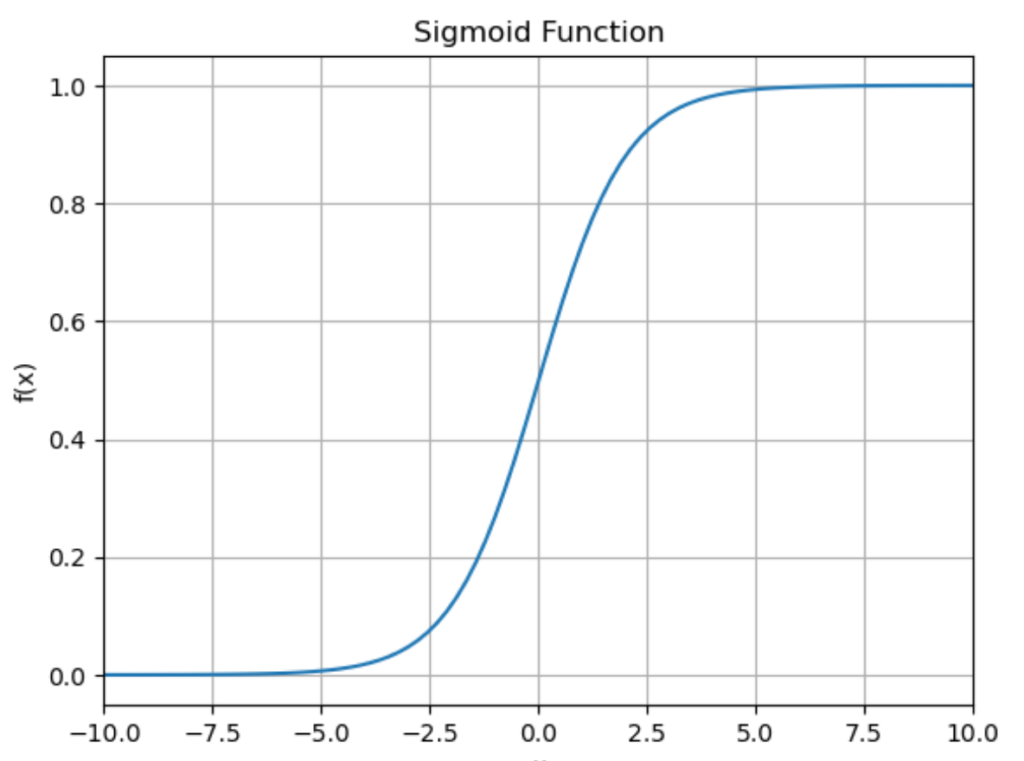
シグモイド関数を使って確率を表す
次に今計算した \(z_1,z_2,…,z_5\) をそれぞれシグモイド関数に入力します。シグモイド関数は下の式で表される関数です。
シグモイド関数:
\(h(z) = \frac{1}{1+\exp(-z)}\)
なお \(\exp(x)\) は \(e^x\) を表す。
シグモイド関数に入力して得られたものをそれぞれ \(p_1,p_2,..,p_5\) とすると、すなわち
\(p_1 = \frac{1}{1+\exp(-z_1)}= \frac{1}{1+\exp(-a_0-a_1x_{11}-a_2x_{12})}\)
\(p_2 = \frac{1}{1+\exp(-z_2)}= \frac{1}{1+\exp(-a_0-a_1x_{21}-a_2x_{22})}\)
\(p_3 = \frac{1}{1+\exp(-z_3)}= \frac{1}{1+\exp(-a_0-a_1x_{31}-a_2x_{32})}\)
\(p_4 = \frac{1}{1+\exp(-z_4)}= \frac{1}{1+\exp(-a_0-a_1x_{41}-a_2x_{42})}\)
\(p_5 = \frac{1}{1+\exp(-z_5)}= \frac{1}{1+\exp(-a_0-a_1x_{51}-a_2x_{52})}\)
を計算します。例えば \((a_0,a_1,a_2)=(0,0.02,-0.04)\) とすると
\(p_1 = \frac{1}{1+\exp(-0.74)}=0.677\)
\(p_2 = \frac{1}{1+\exp(-1.04)}=0.739\)
\(p_3 = \frac{1}{1+\exp(-1.00)}=0.731\)
\(p_4 = \frac{1}{1+\exp(-1.12)}=0.754\)
\(p_5 = \frac{1}{1+\exp(-1.06)}=0.743\) (小数第位を四位を四捨五入)
となります。ロジスティック回帰ではここで得られた\(p\)を確率として考えます。すなわち
データ1が男性である確率は0.677である。
データ2が男性である確率は0.739である。
データ3が男性である確率は0.731である。
データ4が男性である確率は0.754である。
データ5が男性である確率は0.743である。
ということを表しています。しかしこの結果を見ると全然正しく予測できていないですね。今パラメータを \((a_0,a_1,a_2)=(0,0.02,-0.04)\) と設定していますが、パラメータを変更する必要がありそうです。
重み付き和 \(z_i\) は1以上の値を取ったりマイナスの値を取ったりするので、確率として解釈することができません。そこで登場するのがシグモイド関数です。シグモイド関数はどんな実数が入力されても必ず0以上1以下の値を返す関数なので、出力値を確率として解釈することができます。

データのような結果になる確率を計算する
それではここからどのようにパラメータを変更していけば良いのかについて話していきます。これを考えるために「データ \(i\) が男性である確率が \(p_i\) で表される中で、データのような結果が実際に起こる確率」を考えていきます。
より詳しく説明します。今データ1~データ5が男性である確率がそれぞれ \((p_1,p_2,p_3,p_4,p_5)\) で表されています。実際には
データ1:男性
データ2:女性
データ3:男性
データ4:男性
データ5:女性
なんですが、確率が \((p_1,p_2,p_3,p_4,p_5)\) のもとでこのような結果になる確率は
\(p_1\times(1-p_2)\times p_3\times p_4\times(1-p_5)\)
と計算できます。
上の式の説明:
上で言っていることをを言い換えると
「データ1が男性かつデータ2が女性かつデータ3が男性かつデータ4が男性かつデータ5が女性である確率を計算したい」
となります。データ1が男性である確率は \(p_1\) なのは良いんですが、データ2が女性である確率はすなわちデータ2が男性でない確率なので \(1-p_2\) で表されます。またデータ1が男性かつデータ2が女性である確率は互いの確率の積で表すことができるので \(p_1(1-p_2)\) と計算できます。以上のことをデータ1~データ5に対して計算すれば今考えている事象が起こる確率は \(p_1\times(1-p_2)\times p_3\times p_4\times(1-p_5)\) となることが分かります。
例えば \((p_1,p_2,p_3,p_4,p_5)=(0.677,0.739,0.731,0.754,0.743)\) のとき、データ1から順に男性、女性、男性、男性、女性である確率は
\(p_1\times(1-p_2)\times p_3\times p_4\times(1-p_5)\)
\(=0.677 \times (1-0.739) \times 0.731 \times 0.754 \times (1-0.743)\)
\(= 0.0250\) (小数第四位を四捨五入)
と計算できます。つまりこれは
データ1が男性、データ2が女性、データ3が男性、データ4が男性、データ5が女性となる確率は0.025である
ということを表しています。ほぼ0なので、\(p_1,…,p_5\) の値は適切ではなさそうです。\(a_0,a_1,a_2\) を色々動かせば \(p_1,…,p_5\) の値も変わるので、ロジスティック回帰では \(p_1\times(1-p_2)\times p_3\times p_4\times(1-p_5)\) を最大にするようなパラメータ \(a_0,a_1,a_2\) を探します。
確率の式を変形する
それでは次に今考えていた下記の式を変形していきます。
\(p_1\times(1-p_2)\times p_3\times p_4\times(1-p_5)\)
変形その1
この式を\(y,p\)を使って表します。結論以下の式で表すことができます。
\(p_1^{y_1}(1-p_1)^{1-y_1}\times p_2^{y_2}(1-p_2)^{1-y_2}\times \cdots \times p_5^{y_5}(1-p_5)^{1-y_5}\)
本当にこの式で表せるのか1つずつ見ていきましょう。
データ1 \((y_1=1)\):\(p_1^{y_1}(1-p_1)^{1-y_1}=(p_1)^1\times(1-p_1)^0=p_1\)
データ2 \((y_2=0)\):\(p_2^{y_2}(1-p_2)^{1-y_2}=(p_2)^0\times(1-p_2)^1=1-p_2\)
データ3 \((y_3=1)\):\(p_3^{y_3}(1-p_3)^{1-y_3}=(p_3)^1\times(1-p_3)^0=p_3\)
データ4 \((y_4=1)\):\(p_4^{y_4}(1-p_4)^{1-y_4}=(p_4)^1\times(1-p_4)^0=p_4\)
データ5 \((y_5=0)\):\(p_5^{y_5}(1-p_5)^{1-y_5}=(p_5)^0\times(1-p_5)^1=1-p_5\)
ちゃんと正しく変形できていることが分かります。このように変形することで後々表記するのが楽になります。
この式はベルヌーイ分布の確率質量関数です。
\(P(X=k)=p^{k}(1-p)^{1-k}\)
ベルヌーイ分布は確率\(p\)で1、確率\(1-p\)で0を取る確率分布です。
変形その2
次にこの式の対数を取りましょう。
\(\log\{p_1^{y_1}(1-p_1)^{1-y_1}\times p_2^{y_2}(1-p_2)^{1-y_2}\times \cdots \times p_5^{y_5}(1-p_5)^{1-y_5}\}\)
\(=\sum\limits_{i=1}^{5}\log\{p_i^{y_i}(1-p_i)^{1-y_i}\}\)
\(=\sum\limits_{i=1}^{5}\{\log p_i^{y_i}+\log(1-p_i)^{1-y_i}\}\)
\(=\sum\limits_{i=1}^{5}\{y_i\log p_i+(1-y_i)\log(1-p_i)\}\)
上記のように変形できました。対数を取ることで掛け算で表されていたものを足し算で表すことができます。この後微分を計算するんですが、足し算で表されていた方が計算しやすいので対数を取っています。
また今回の目標は\(p_1^{y_1}(1-p_1)^{1-y_1}\times p_2^{y_2}(1-p_2)^{1-y_2}\times \cdots \times p_5^{y_5}(1-p_5)^{1-y_5}\)が最大となるときを見つけることですが、対数関数は単調増加関数なので\(p_1^{y_1}(1-p_1)^{1-y_1}\times p_2^{y_2}(1-p_2)^{1-y_2}\times \cdots \times p_5^{y_5}(1-p_5)^{1-y_5}\)が最大となるとき\(\sum\limits_{i=1}^{5}\{y_i\log p_i+(1-y_i)\log(1-p_i)\}\)も最大となります。
従ってロジスティック回帰では下の式を最大化するようなパラメータ\(a_0,a_1,a_2\)を探します。
\(\sum\limits_{i=1}^{5}\{y_i\log p_i+(1-y_i)\log(1-p_i)\}\)
ちょっと前に登場した \(p_1\times(1-p_2)\times p_3\times p_4\times(1-p_5)\) は尤度と呼ばれます。尤度はデータが与えられたときに、そのデータを生成したと考えられる確率のパラメータが、どれだけ「もっともらしいか」を表す指標です。今回の例で言うと\(p_1,p_2,…,p_5\)が与えられたときに、データのような結果(データ1が男性でデータ2が女性で…)になる確率がどれくらいになるかが尤度で \(p_1\times(1-p_2)\times p_3\times p_4\times(1-p_5)\) と計算できます。尤度が大きいほど \(p_1,..,p_5\) がもっともらしいことを表します。この例では尤度が0.025なので全然もっともらしくないです。
今回はこの尤度が最大になるようなパラメータ \(a_0,a_1,a_2\) を求めることが目的ですが、これは最尤推定と呼ばれます。最尤推定はだいたい尤度の対数を取ってから微分して最適パラメータを求めます。対数を取る理由は先ほども説明したように積の形から和の形で表すことができ、微分が楽に計算できるからです。これを尤度の対数を取ったものを対数尤度と言ったりします。
ロジスティック回帰では実はこの最尤推定を行って最適なパラメータを求めています。
変形その3
最後の変形は超単純で、今計算した対数尤度にマイナスを掛け算します。すなわち
\(L = -\sum\limits_{i=1}^{5}\{y_i\log p_i+(1-y_i)\log(1-p_i)\}\)
とします。これ以降上の式を \(L\) とします。ちなみに \((p_1,p_2,p_3,p_4,p_5)=(0.677,0.739,0.731,0.754,0.743)\) のとき \(L\) の値は
\(L = -\sum\limits_{i=1}^{5}\{y_i\log p_i+(1-y_i)\log(1-p_i)\}\)
\(= -\log0.677-\log0.261-\log0.731-\log0.754-\log0.257\)
\(=3.69\) (小数第三位を四捨五入)
と計算できます。ロジスティック回帰では変形その2で得られた対数尤度を最大化することが目的でしたが、これはすなわち \(L\) を最小化することと同じです。
ここまでやってきたことをまとめると、ロジスティック回帰では下の式を最小化するようなパラメータ \(a_0,a_1,a_2\) を求めることを目的とします。
最小化したい式:
\(L = -\sum\limits_{i=1}^{5}\{y_i\log p_i+(1-y_i)\log(1-p_i)\}\)
微分を計算する
関数の最小値を求めるために \(L\) をパラメータ \(a_0,a_1,a_2\) で微分しましょう。 \(a_0\) で偏微分した場合、\(a_1\) で偏微分した場合、\(a_2\) で偏微分した場合それぞれについて見ていきます。
\(a_0\) で \(L\) を偏微分する
\(L\) を \(a_0\) で偏微分した式、すなわち \(\frac{\partial L}{\partial a_0}\) を求めます。
\(L= -\sum\limits_{i=1}^{5}\{y_i\log p_i+(1-y_i)\log(1-p_i)\}\)
\(p_i = \frac{1}{1+\exp(-z_i)}\)
\(z_i = a_0+a_1x_{i1}+a_2x_{i2}\)
ところが直接 \(\frac{\partial L}{\partial a_0}\) を計算しようとすると、\(z_i\) の式を \(p_i\) に代入してそれを \(L\) に代入して複雑な式を微分する必要がありめちゃめちゃ大変です。
そのため連鎖律を使って \(\frac{\partial L}{\partial a_0}\) を計算します。具体的には
\(\frac{\partial L}{\partial a_0}=\frac{\partial L}{\partial p_1}\frac{dp_1}{dz_1}\frac{\partial z_1}{\partial a_0}+\frac{\partial L}{\partial p_2}\frac{dp_2}{dz_2}\frac{\partial z_2}{\partial a_0}\)
\(+\frac{\partial L}{\partial p_3}\frac{dp_3}{dz_3}\frac{\partial z_3}{\partial a_0}+\frac{\partial L}{\partial p_4}\frac{dp_4}{dz_4}\frac{\partial z_4}{\partial a_0}+\frac{\partial L}{\partial p_5}\frac{dp_5}{dz_5}\frac{\partial z_5}{\partial a_0}\)
を計算します。それぞれ計算していきます。
\(\frac{\partial L}{\partial p_i} = -\frac{y_i}{p_i} +\frac{1-y_i}{1-p_i}=\frac{-y_i+p_iy_i+p_i-p_iy_i}{p_i(1-p_i)}=\frac{p_i-y_i}{p_i(1-p_i)}\)
\(\frac{dp_i}{dz_i}=-\frac{-\exp(-z_i)}{(1+\exp(-z_i))^2} = \frac{1}{1+\exp(-z_i)}\times\frac{\exp(-z_i)}{1+\exp(-z_i)}=p_i(1-p_i)\)
\(\frac{\partial z_i}{\partial a_0}=1\)
従って
\(\frac{\partial L}{\partial p_i}\frac{dp_i}{dz_i}\frac{\partial z_i}{\partial a_0}=\frac{p_i-y_i}{p_i(1-p_i)}\times p_i(1-p_i)\times 1 = p_i-y_i\)
となります。以上より
\(\frac{\partial L}{\partial a_0}=\sum\limits_{i=1}^{5}(p_i-y_i)\)
と計算することができました。
\(a_1\) で \(L\) を偏微分する
\(L\) を \(a_1\) で偏微分した式、すなわち \(\frac{\partial L}{\partial a_1}\) を求めます。
\(L= -\sum\limits_{i=1}^{5}\{y_i\log p_i+(1-y_i)\log(1-p_i)\}\)
\(p_i = \frac{1}{1+\exp(-z_i)}\)
\(z_i = a_0+a_1x_{i1}+a_2x_{i2}\)
こちらも連鎖律を使って \(\frac{\partial L}{\partial a_1}\) を計算します。具体的には
\(\frac{\partial L}{\partial a_1}=\frac{\partial L}{\partial p_1}\frac{dp_1}{dz_1}\frac{\partial z_1}{\partial a_1}+\frac{\partial L}{\partial p_2}\frac{dp_2}{dz_2}\frac{\partial z_2}{\partial a_1}\)
\(+\frac{\partial L}{\partial p_3}\frac{dp_3}{dz_3}\frac{\partial z_3}{\partial a_1}+\frac{\partial L}{\partial p_4}\frac{dp_4}{dz_4}\frac{\partial z_4}{\partial a_1}+\frac{\partial L}{\partial p_5}\frac{dp_5}{dz_5}\frac{\partial z_5}{\partial a_1}\)
を計算します。それぞれ計算していきます。
\(\frac{\partial L}{\partial p_i} = -\frac{y_i}{p_i} +\frac{1-y_i}{1-p_i}=\frac{-y_i+p_iy_i+p_i-p_iy_i}{p_i(1-p_i)}=\frac{p_i-y_i}{p_i(1-p_i)}\)
\(\frac{dp_i}{dz_i}=-\frac{-\exp(-z_i)}{(1+\exp(-z_i))^2} = \frac{1}{1+\exp(-z_i)}\times\frac{\exp(-z_i)}{1+\exp(-z_i)}=p_i(1-p_i)\)
\(\frac{\partial z_i}{\partial a_1}=x_{i1}\)
従って
\(\frac{\partial L}{\partial p_i}\frac{dp_i}{dz_i}\frac{\partial z_i}{\partial a_0}=\frac{p_i-y_i}{p_i(1-p_i)}\times p_i(1-p_i)\times x_{i1} = (p_i-y_i)x_{i1}\)
となります。以上より
\(\frac{\partial L}{\partial a_1}=\sum\limits_{i=1}^{5}\{(p_i-y_i)x_{i1}\}\)
と計算することができました。
\(a_2\) で \(L\) を偏微分する
\(L\) を \(a_2\) で偏微分した式、すなわち \(\frac{\partial L}{\partial a_2}\) を求めます。
\(L= -\sum\limits_{i=1}^{5}\{y_i\log p_i+(1-y_i)\log(1-p_i)\}\)
\(p_i = \frac{1}{1+\exp(-z_i)}\)
\(z_i = a_0+a_1x_{i1}+a_2x_{i2}\)
こちらも連鎖律を使って \(\frac{\partial L}{\partial a_2}\) を計算します。具体的には
\(\frac{\partial L}{\partial a_2}=\frac{\partial L}{\partial p_1}\frac{dp_1}{dz_1}\frac{\partial z_1}{\partial a_2}+\frac{\partial L}{\partial p_2}\frac{dp_2}{dz_2}\frac{\partial z_2}{\partial a_2}\)
\(+\frac{\partial L}{\partial p_3}\frac{dp_3}{dz_3}\frac{\partial z_3}{\partial a_2}+\frac{\partial L}{\partial p_4}\frac{dp_4}{dz_4}\frac{\partial z_4}{\partial a_2}+\frac{\partial L}{\partial p_5}\frac{dp_5}{dz_5}\frac{\partial z_5}{\partial a_2}\)
を計算します。それぞれ計算していきます。
\(\frac{\partial L}{\partial p_i} = -\frac{y_i}{p_i} +\frac{1-y_i}{1-p_i}=\frac{-y_i+p_iy_i+p_i-p_iy_i}{p_i(1-p_i)}=\frac{p_i-y_i}{p_i(1-p_i)}\)
\(\frac{dp_i}{dz_i}=-\frac{-\exp(-z_i)}{(1+\exp(-z_i))^2} = \frac{1}{1+\exp(-z_i)}\times\frac{\exp(-z_i)}{1+\exp(-z_i)}=p_i(1-p_i)\)
\(\frac{\partial z_i}{\partial a_2}=x_{i2}\)
従って
\(\frac{\partial L}{\partial p_i}\frac{dp_i}{dz_i}\frac{\partial z_i}{\partial a_0}=\frac{p_i-y_i}{p_i(1-p_i)}\times p_i(1-p_i)\times x_{i1} = (p_i-y_i)x_{i2}\)
となります。以上より
\(\frac{\partial L}{\partial a_2}=\sum\limits_{i=1}^{5}\{(p_i-y_i)x_{i2}\}\)
と計算することができました。
微分した式を行列・ベクトルを使って表してみましょう。
\(X = \begin{pmatrix}1&x_{11}&x_{12} \\ 1&x_{21}&x_{22} \\ 1&x_{31}&x_{32} \\ 1&x_{41}&x_{42} \\ 1&x_{51}&x_{52}\end{pmatrix}, \; a = \begin{pmatrix}a_0\\a_1\\a_2\end{pmatrix}\)
とします。このとき \(Xa\) は
\(Xa = \begin{pmatrix}a_0+a_1x_{11}+a_2x_{12}\\a_0+a_1x_{21}+a_2x_{22}\\a_0+a_1x_{31}+a_2x_{32}\\a_0+a_1x_{41}+a_2x_{42}\\a_0+a_1x_{51}+a_2x_{52}\end{pmatrix}\)
となります。これを見ると \(Xa\) の \(i\) 行目は \(z_i\) になっていることが分かります。続いてシグモイド関数を \(h(z)\) と表すことにします。すなわち
\(h(Xa) = \begin{pmatrix}\frac{1}{1+\exp(a_0+a_1x_{11}+a_2x_{12})} \\ \frac{1}{1+\exp(a_0+a_1x_{21}+a_2x_{22})} \\ \frac{1}{1+\exp(a_0+a_1x_{31}+a_2x_{32})} \\ \frac{1}{1+\exp(a_0+a_1x_{41}+a_2x_{42})} \\ \frac{1}{1+\exp(a_0+a_1x_{51}+a_2x_{52})}\end{pmatrix} = \begin{pmatrix}p_1\\p_2\\p_3\\p_4\\p_5\end{pmatrix}\)
となり \(h(Xa)\) が確率 \(p\) を表します。ここでさらに
\(x_0 = \begin{pmatrix}1\\1\\1\\1\\1\end{pmatrix} \; x_1 = \begin{pmatrix}x_{11}\\x_{21}\\x_{31}\\x_{41}\\x_{51}\end{pmatrix} \; x_2 = \begin{pmatrix}x_{12}\\x_{22}\\x_{32}\\x_{42}\\x_{52}\end{pmatrix} \; y = \begin{pmatrix}y_1\\y_2\\y_3\\y_4\\y_5\end{pmatrix}\)
とすると
\(x_0^\top (h(Xa)-y) = \begin{pmatrix}1&1&1&1&1\end{pmatrix}\begin{pmatrix}p_1-y_1\\p_2-y_2\\p_3-y_3\\p_4-y_4\\p_5-y_5\end{pmatrix} = \sum\limits_{i=1}^5(p_i-y_i)=\frac{\partial L}{\partial a_0}\)
\(x_1^\top (h(Xa)-y) = \begin{pmatrix}x_{11}\;x_{21}\;x_{31}\;x_{41}\;x_{51}\end{pmatrix}\begin{pmatrix}p_1-y_1\\p_2-y_2\\p_3-y_3\\p_4-y_4\\p_5-y_5\end{pmatrix} = \sum\limits_{i=1}^5\{(p_i-y_i)x_{i1}\}=\frac{\partial L}{\partial a_1}\)
\(x_2^\top (h(Xa)-y) = \begin{pmatrix}x_{12}\;x_{22}\;x_{32}\;x_{42}\;x_{52}\end{pmatrix}\begin{pmatrix}p_1-y_1\\p_2-y_2\\p_3-y_3\\p_4-y_4\\p_5-y_5\end{pmatrix} = \sum\limits_{i=1}^5\{(p_i-y_i)x_{i2}\}=\frac{\partial L}{\partial a_2}\)
が成り立ちます。以上より微分した式を行列・ベクトルを使って表すと
\(\frac{\partial L}{\partial a_i} = x_i^\top(h(Xa)-y)\)
となります。
微分した式が0になる点を求めるのが困難
関数の最大・最小を求めるときによくある手法は微分した式が0になる点を探すという手法です。しかし今回は式が複雑なので \(\frac{\partial L}{\partial a_0},\frac{\partial L}{\partial a_1},\frac{\partial L}{\partial a_2}\) が全て0になる\(a_0,a_1,a_2\)の組を探すのが困難です。
ということで別の手法を用いる必要があります。今回は勾配降下法を使って最適なパラメータを決定する方法について説明していきます。
\(\frac{\partial L}{\partial a_0}=\frac{\partial L}{\partial a_1}=\frac{\partial L}{\partial a_2}=0\) になる点を求めようとすると
\(\frac{\partial L}{\partial a_0} = \sum\limits_{i=1}^5(\frac{1}{1+\exp(-a_0-a_1x_{i1}-a_2x_{i2})}-y_i)=0\)
\(\frac{\partial L}{\partial a_1} = \sum\limits_{i=1}^5\{(\frac{1}{1+\exp(-a_0-a_1x_{i1}-a_2x_{i2})}-y_i)x_{i1}\}=0\)
\(\frac{\partial L}{\partial a_2} = \sum\limits_{i=1}^5\{(\frac{1}{1+\exp(-a_0-a_1x_{i1}-a_2x_{i2})}-y_i)x_{i2}\}=0\)
上の3つの連立方程式を解かないといけないんですが、ちょっと厳しそうですね。
勾配降下法を使って最適なパラメータを求める
大雑把に説明すると、勾配降下法は微分した値を使って最適値にどんどん近づいていく手法です。詳しい話は別の記事で解説しているのでそちらを見てみてください。
今回は下の式に従って \(a_0,a_1,a_2\) をどんどん更新していきます。なおここで登場する \(\eta\) は学習率を表していて、自分で決めるパラメータです。
\(a_0 \to a_0 – \eta\frac{\partial L}{\partial a_0}\)
\(a_1 \to a_1 – \eta\frac{\partial L}{\partial a_1}\)
\(a_2 \to a_2 – \eta\frac{\partial L}{\partial a_2}\)
\(\frac{\partial L}{\partial a_0},\frac{\partial L}{\partial a_1},\frac{\partial L}{\partial a_2}\) は先ほど計算したので代入しましょう。
\(a_0 \to a_0 – \eta\sum\limits_{i=1}^5(p_i-y_i)\)
\(a_1 \to a_1 – \eta\sum\limits_{i=1}^5(p_i-y_i)x_{i1}\)
\(a_2 \to a_2 – \eta\sum\limits_{i=1}^5(p_i-y_i)x_{i2}\)
ということでパラメータ更新の式が上のように得られました。この式に従ってパラメータを繰り返し更新していきます。今回の例を使って具体的に計算してみましょう。各文字の値は
\((x_{11},x_{21},x_{31},x_{41},x_{51})=(177,158,170,168,163)\)
\((x_{12},x_{22},x_{32},x_{42},x_{52})=(70,53,60,56,55)\)
\((a_0,a_1,a_2)=(0,0.02,-0.04)\)
\((p_1,p_2,p_3,p_4,p_5)=(0.677,0.739,0.731,0.754,0.743)\)
\((y_1,y_2,y_3,y_4,y_5)=(1,0,1,1,0)\)
\(\eta = 0.1\)
とすると更新後のパラメータ \(a_0,a_1,a_2\) の値は
\(a_0 = 0-0.1 \times \{(0.677-1)+\cdots+(0.743-0)\}\)
\(=0 -0.1 \times 0.644 = -0.0644\)
\(a_1 = 0.02-0.1 \times \{(0.677-1)\times177+\cdots+(0.743-0)\times163\}\)
\(=0 -0.1 \times 96.332 = -9.6132\)
\(a_1 = -0.04-0.1 \times \{(0.677-1)\times70+\cdots+(0.743-0)\times55\}\)
\(=0 -0.1 \times 27.506 = -2.7906\)
と計算できます。この計算によってパラメータが
\((0,0.02,-0.04) \to (-0.0644,-9.6132,-2.7906)\)
と更新されました。今は1回しか更新していませんが、これを10回、100回、1000回と更新していって最適なパラメータを求めていきます。
ロジスティック回帰を行うときはまずデータを標準化してスケールを合わせるのが一般的です。今回のデータは身長と体重を説明変数に使いましたが、これらはスケールが違うデータなので、上の説明のようにデータをそのまま使って勾配降下法を適用しても良いパラメータが求められない可能性があります。
異常でロジスティック回帰のアルゴリズムの説明を終了します。
おまけ:パラメータ更新の様子を可視化して確認してみる
ロジスティック回帰では勾配降下法を用いてどんどんパラメータ更新していきます。ということでパラメータ更新の様子を可視化して確認してみしょう。
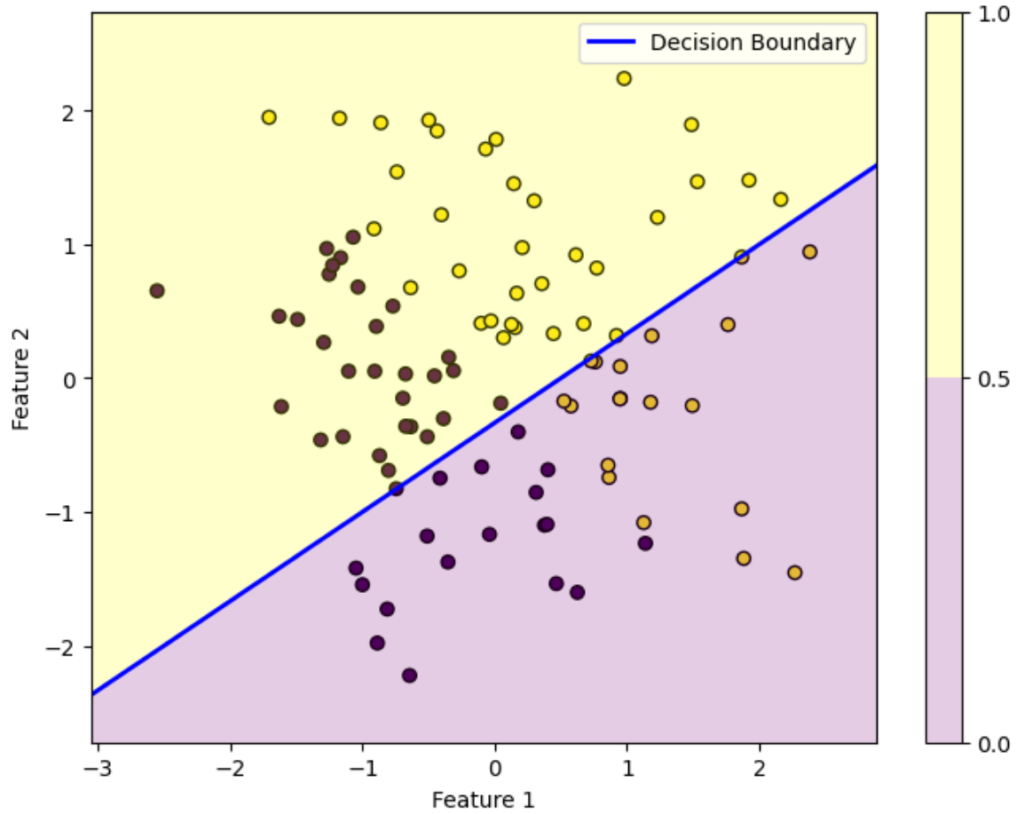
初期パラメータ
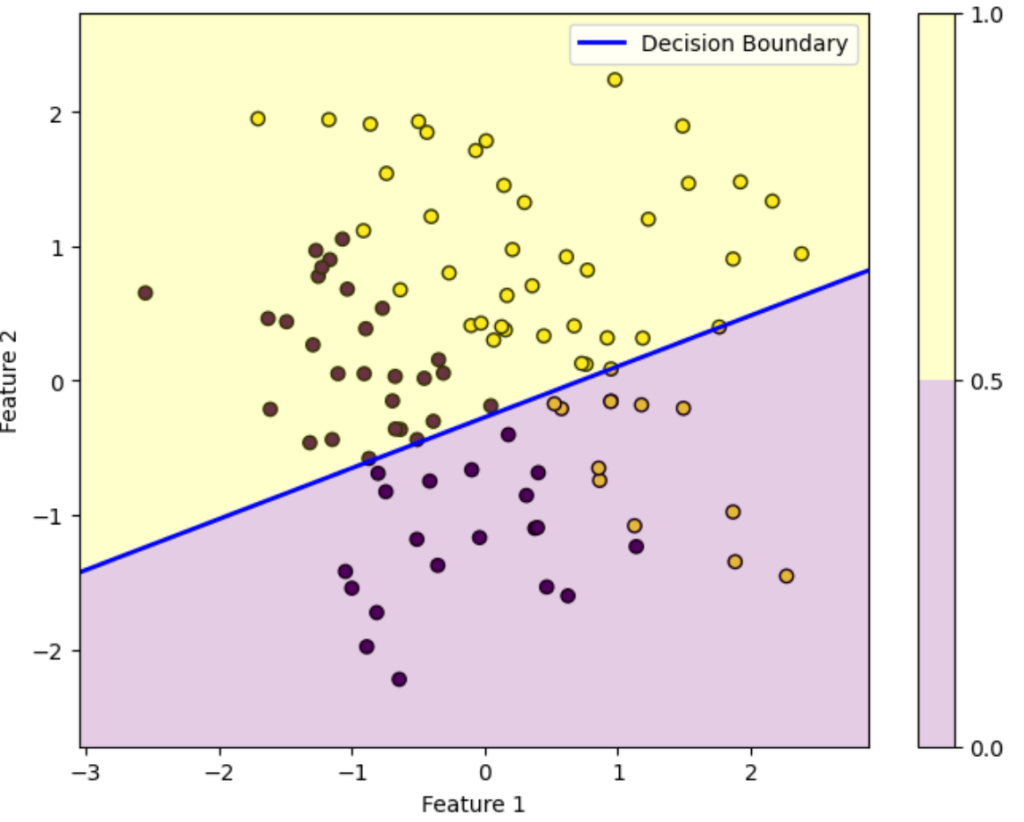
反復10回目
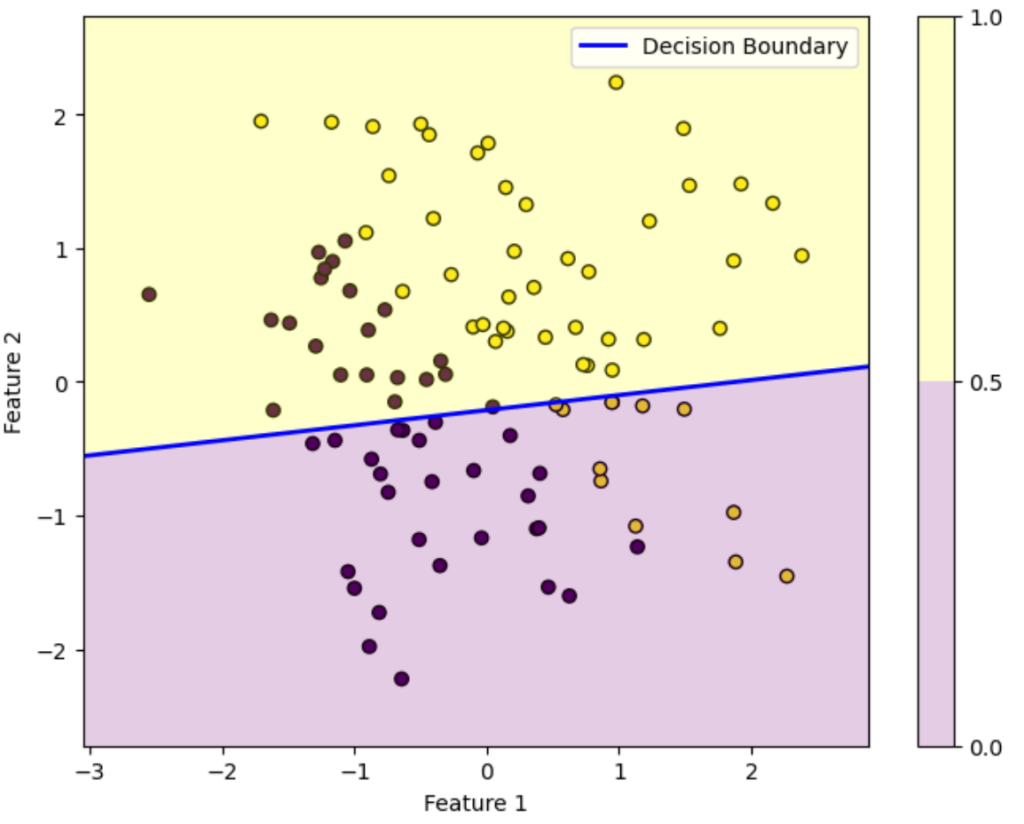
反復20回目
反復30回目
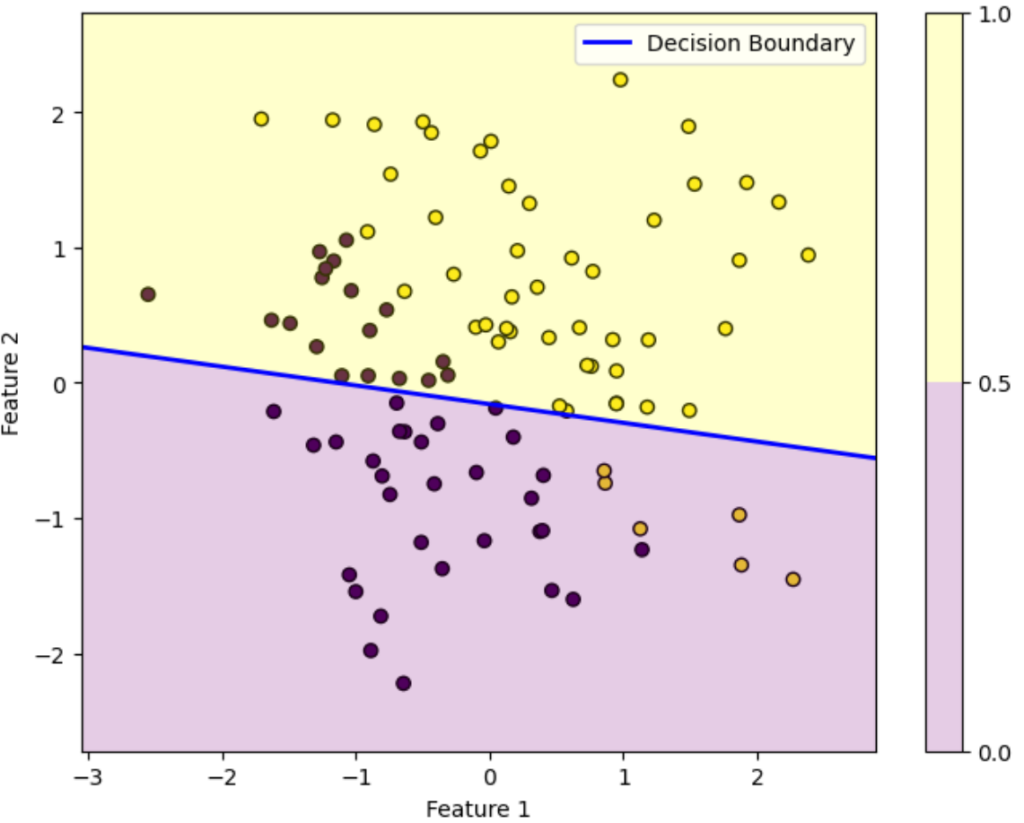
反復40回目
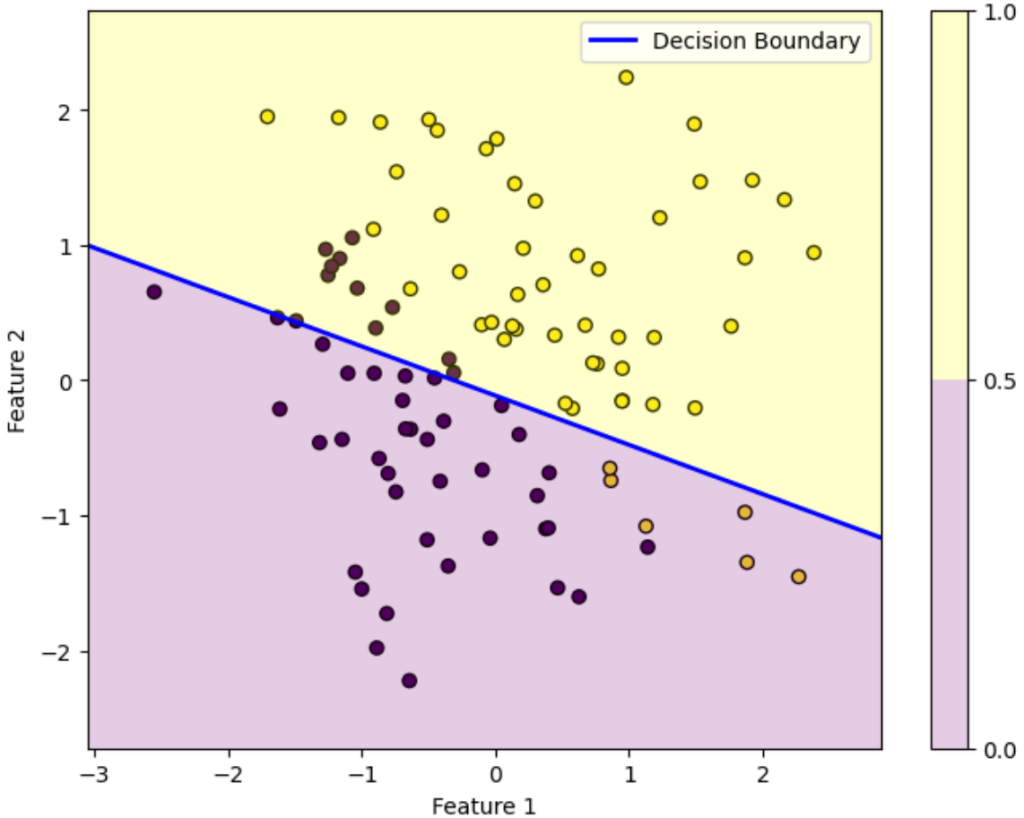
反復50回目
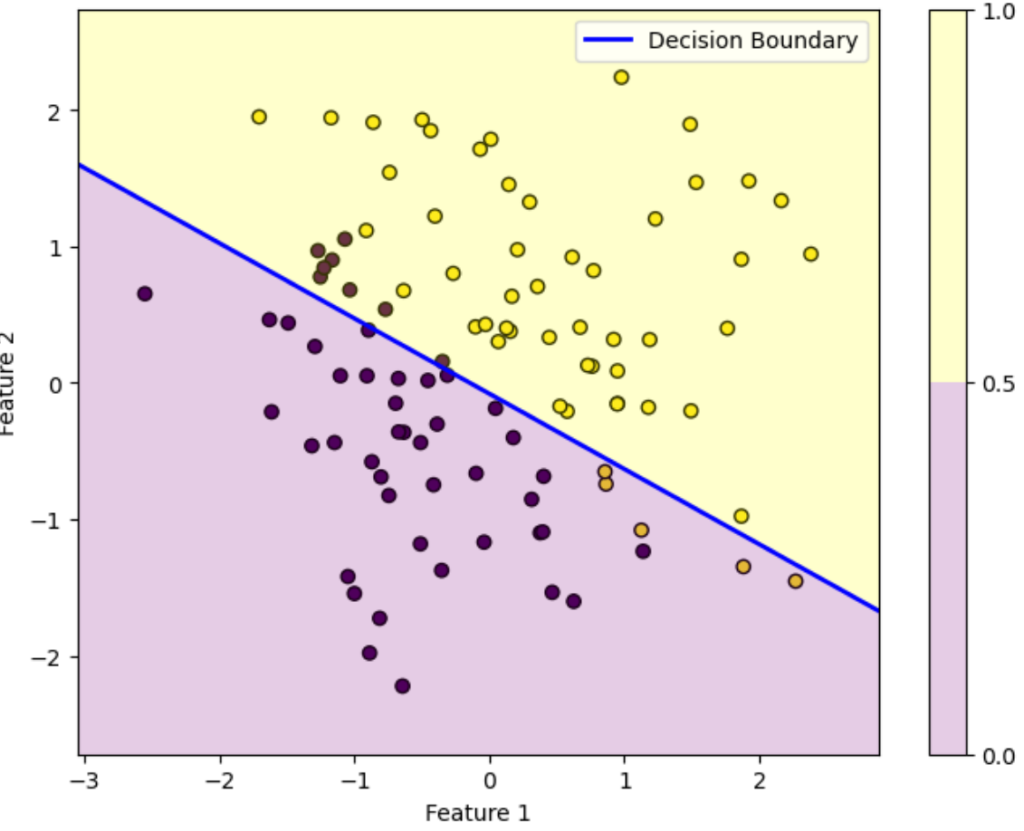
反復60回目
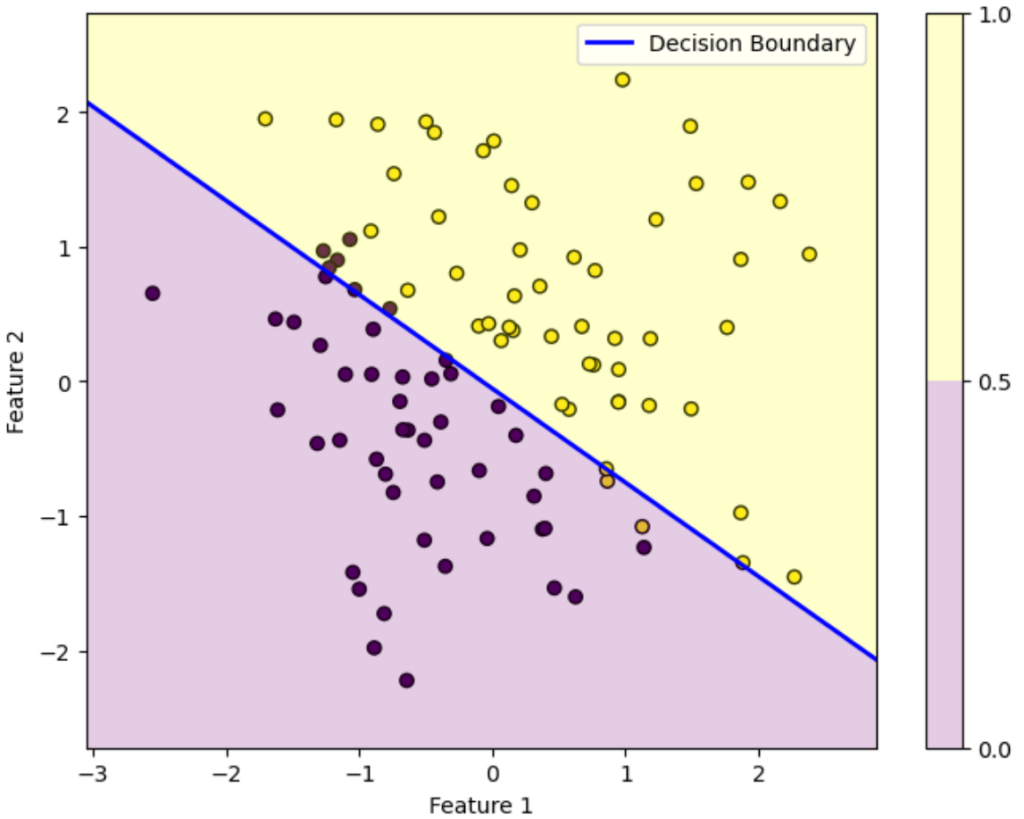
反復70回目
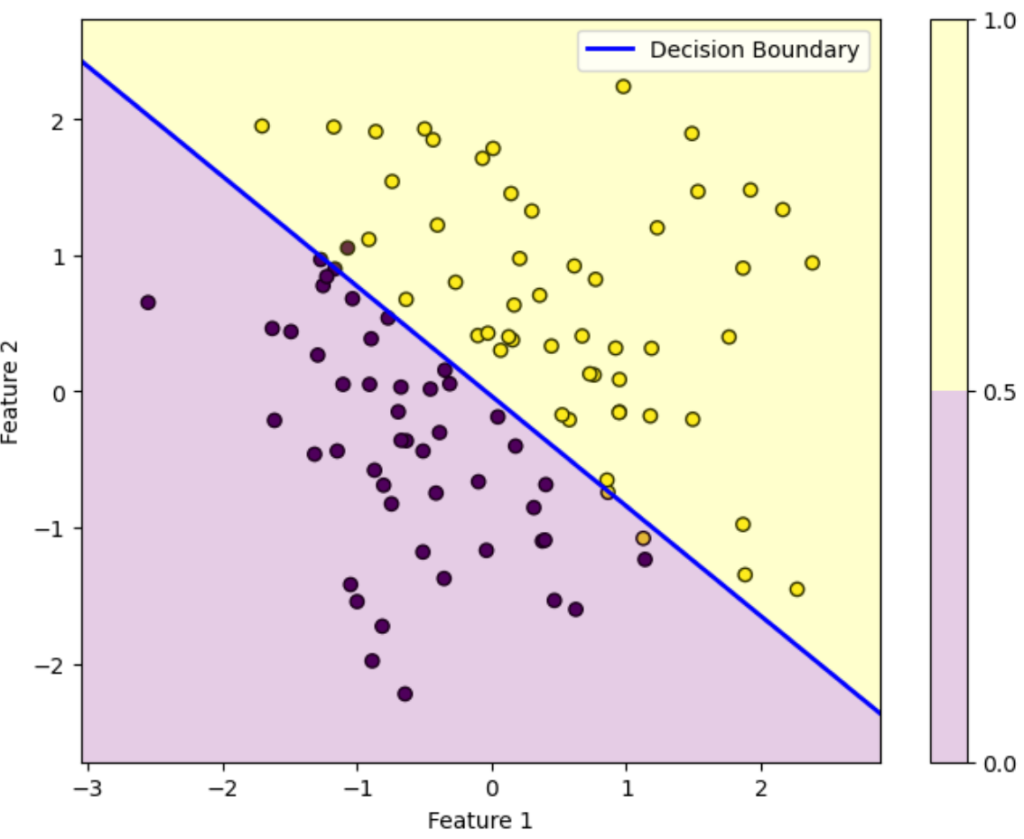
反復80回目
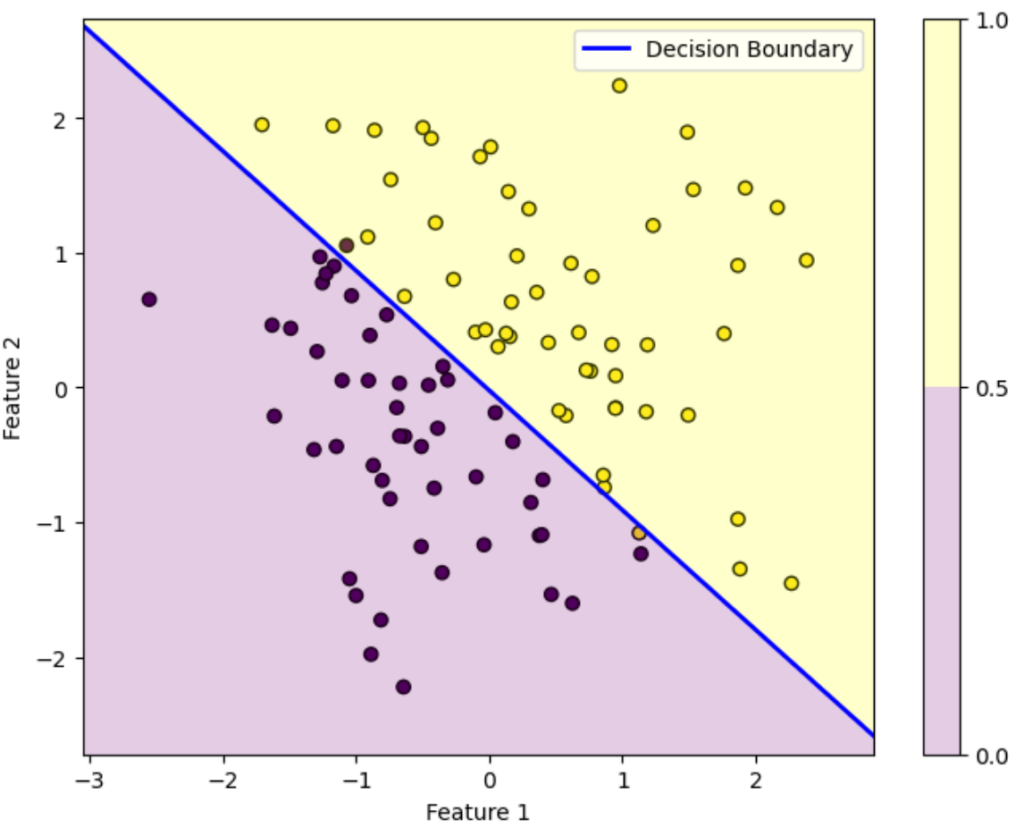
反復90回目
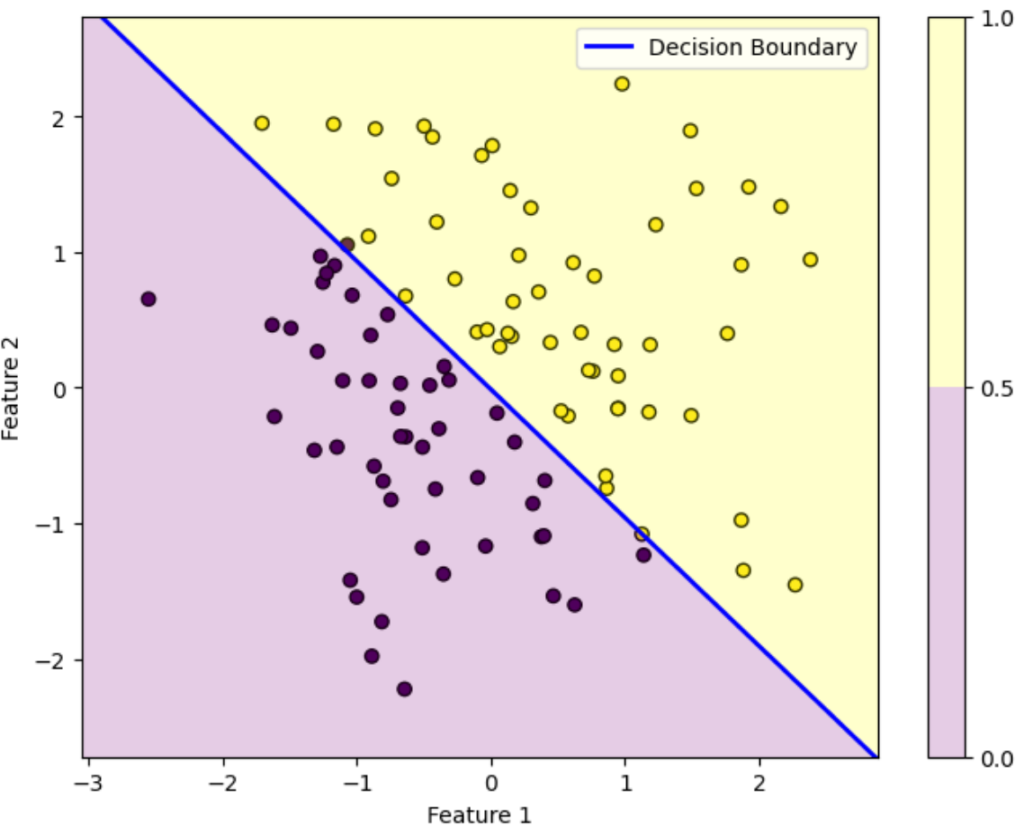
反復100回目
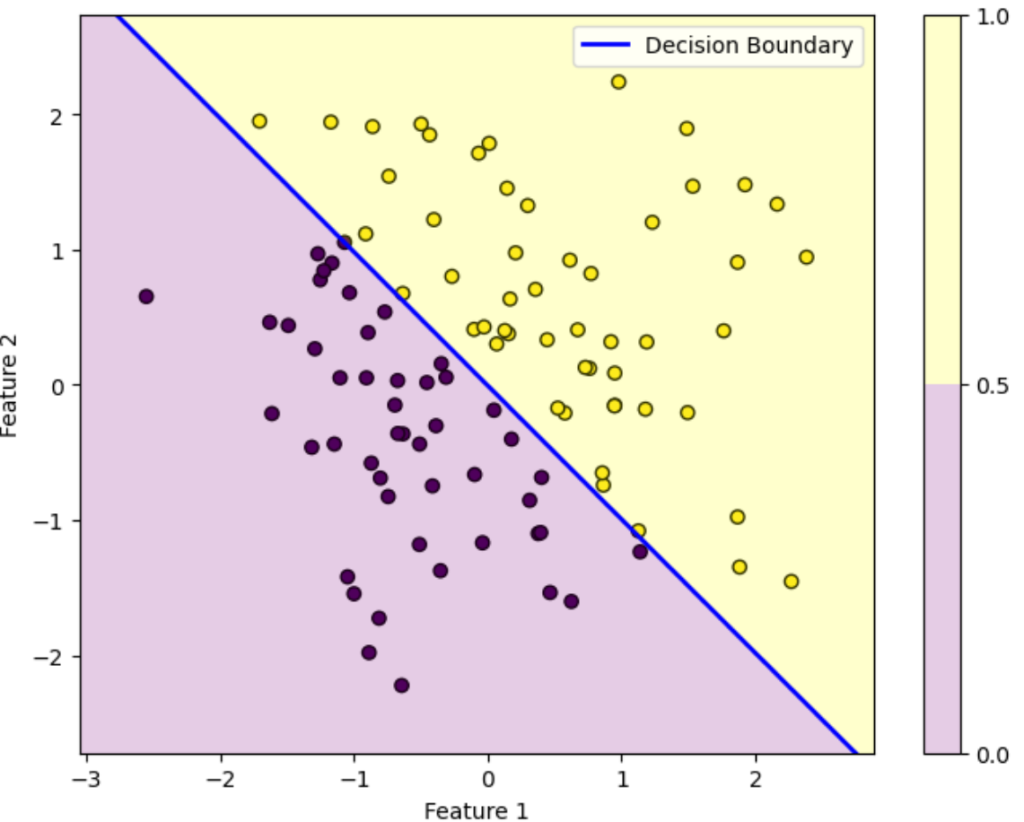
総反復回数:100回
学習率:0.2
初期パラメータ:
\(a_0 = 1\)
\(a_1 = -2\)
\(a_2 = 3\)
この図はデータを黄色のデータか紫色のデータかを判別する様子を表しています。ロジスティック回帰によって得られた確率が0.5を超えている領域は黄色、0.5未満の領域は紫色に塗っています。青い直線は確率がちょうど0.5になる境界を表しています。
初期パラメータの図を見ると全然正しく分類できていないことが分かります。しかし反復を重ねるにつれパラメータが更新されていき、反復100回目を見ると正しく分類できていることが分かります。
このようにロジスティック回帰では最初は全然ダメなパラメータでも更新を重ねるにつれだんだん適切なパラメータになっていくことが上図を見れば分かります。
境界の方程式について考えてみましょう。境界はロジスティックによって得られた確率がちょうど0.5のラインを表しています。確率はシグモイド関数によって表されるので、この境界の方程式は
\(\frac{1}{1+e^{-z}}=0.5\)
となります。下図を見ると分かるように、シグモイド関数は\(z=0\)のときに0.5を取るという性質があります。

ロジスティック回帰ではシグモイド関数に入力する \(z\) が重み付き和 \(a_0+a_1x_1+a_2x_2\) なので、結局境界の方程式は
\(a_0+a_1x_1+a_2x_2=0\)
となります。
おわりに
いかがでしたか。
今回の記事ではロジスティック回帰について解説しました。
今後もこのような機械学習に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
参考文献







