- 最小全域木ってなに?
- 最小全域木問題を整数計画問題として定式化したい…
- 最小全域木問題をpythonで解きたい…
こんにちは!しゅんです!
今回は最小全域木について解説していきます!
最小全域木は最適化やグラフ理論で登場する用語です。この記事では最小全域木を求める問題を整数計画問題として定式化してpythonで解く方法を解説したいと思います。
それではやっていきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
最小全域木ってなに?
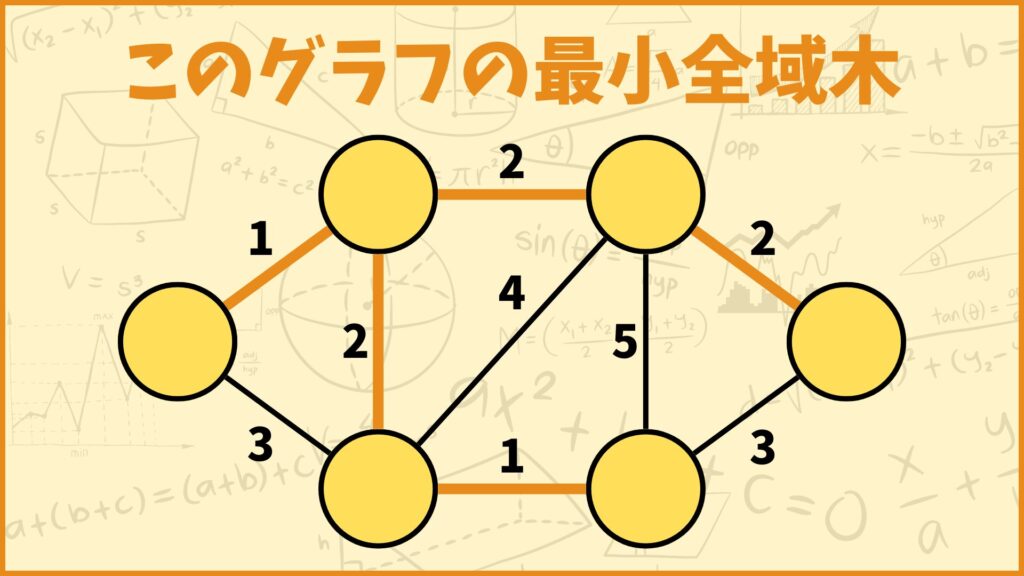
最小全域木は全域木の中でも辺の重みの合計が最小となるものです。例えば上のグラフの最小全域木は橙で塗った辺集合です。
この最小全域木の重みの合計は
\(1+2+1+2+2 = 8\)
となります。
最小全域木問題を整数計画問題として定式化する
パラメータ:
\(V\):頂点集合
\(E\):辺集合
\(c_e\):辺 \(e\) の重み
\(\delta(S)\):頂点集合 \(S\) と \(V\backslash S\) つなぐ辺集合
変数:
\(x_e\):辺 \(e\) を採用するなら1、そうでないなら0を取る0-1変数
目的関数(最小化):
\(\sum\limits_{e \in E}c_ex_e\)
制約条件:
\(\sum\limits_{e \in E}x_e = |V|-1\)
\(\sum\limits_{e \in \delta(S)}x_e\geq 1 \;\;\; (\forall S \subset V, S \ne \emptyset)\)
\(x_e \in \{0,1\} \;\;\; (\forall e \in E)\)
結論上のように定式化することができます。1つずつ解説していきます。
最小全域木問題はクラスカル法やプリム法など、多項式時間で最適解が得られるアルゴリズムが見つかっています。
パラメータ・変数の設定
パラメータ:
\(V\):頂点集合
\(E\):辺集合
\(c_e\):辺 \(e\) の重み
\(\delta(S)\):頂点集合 \(S\) と \(V\backslash S\) つなぐ辺集合
変数:
\(x_e\):辺 \(e\) を採用するなら1、そうでないなら0を取る0-1変数
パラメータとして頂点集合、辺集合、辺の重み、そして \(\delta(S)\) を設定します。\(\delta(S)\) の説明は2つ目の制約条件の所で説明します。
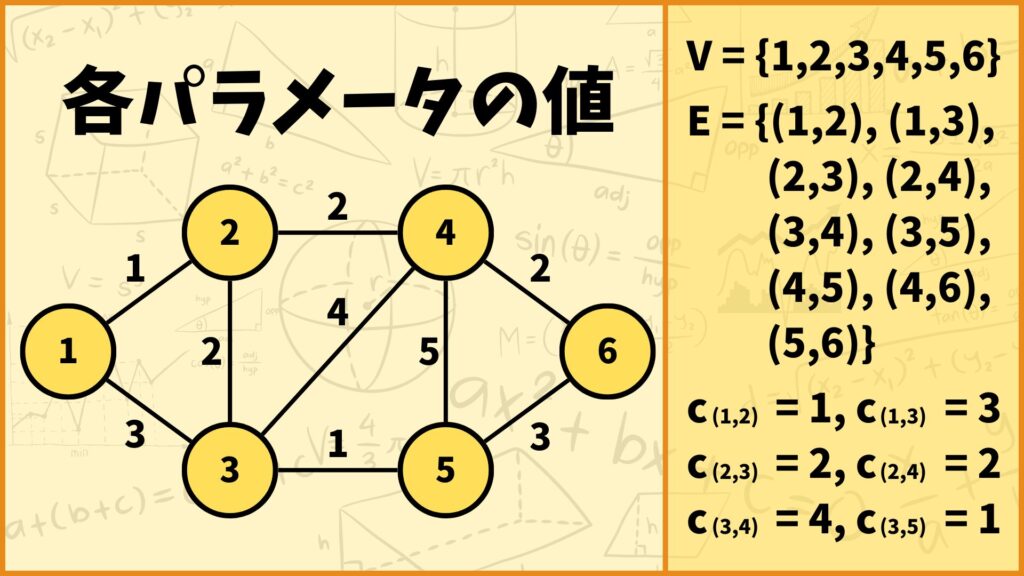
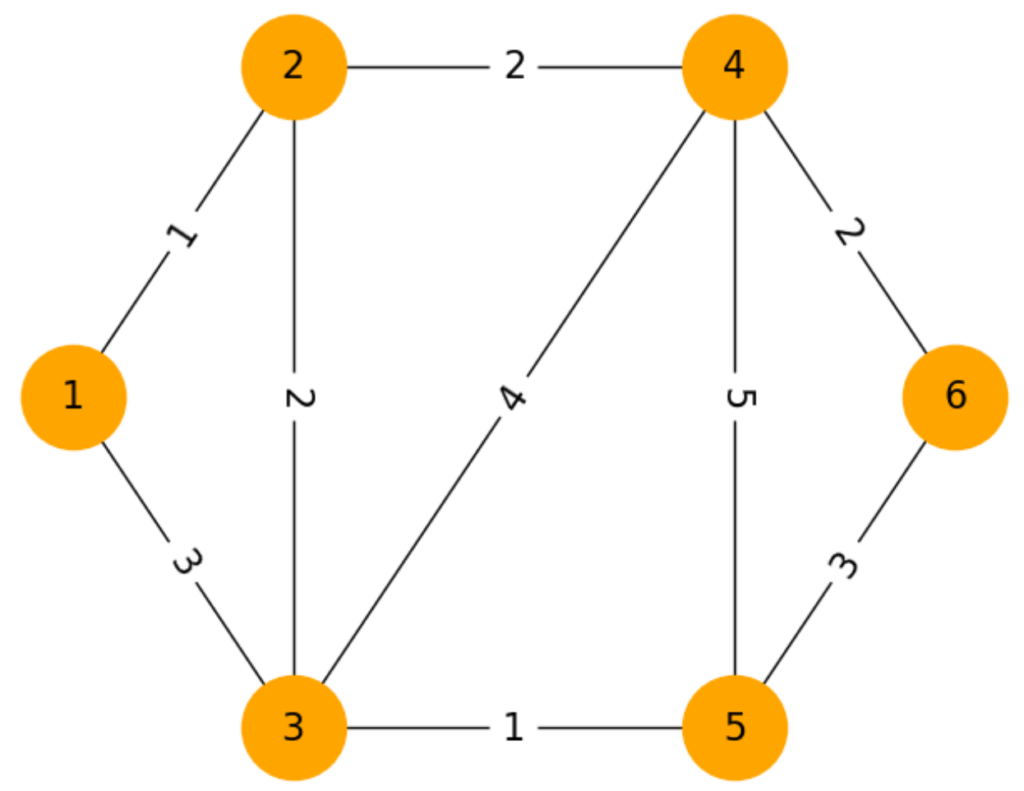
例えば上図の例だと、
\(V = \{1,2,3,4,5,6\}\)
\(E = \{(1,2),(1,3),(2,3),(2,4),(3,4),(3,5),(4,5),(4,6),(5,6)\}\)
\(c_{(1,2)}=1,c_{(1,3)}=3,c_{(2,3)}=2,\)
\(c_{(2,4)}=2,c_{(3,4)}=4,c_{(3,5)}=1,\)
\(c_{(4,5)}=5,c_{(4,6)}=2,c_{(5,6)}=3\)
となります。
また0-1変数として \(x_e\) を用意します。
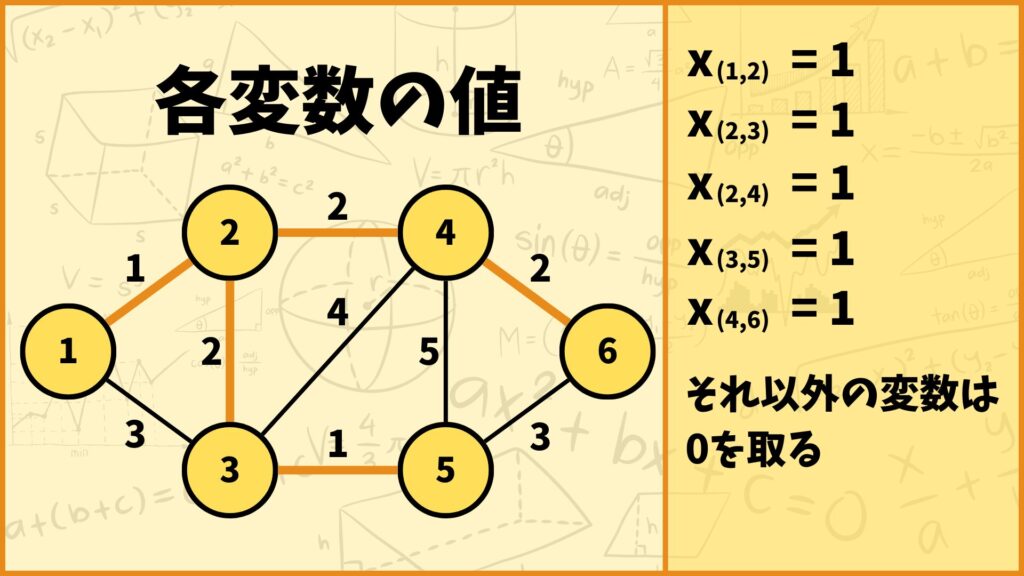
例えば上図の例だと
\(x_{(1,2)}=1\)
\(x_{(2,3)}=1\)
\(x_{(2,4)}=1\)
\(x_{(3,5)}=1\)
\(x_{(4,6)}=1\)
でそれ以外の変数は0を取ります。
目的関数の設定
目的関数(最小化):
\(\sum\limits_{e \in E}c_ex_e\)

例えば上図の例だと、この目的関数値は
\(\sum\limits_{e \in E}c_ex_e\)
\(=c_{(1,2)}x_{(1,2)}+c_{(2,3)}x_{(2,3)}+c_{(2,4)}x_{(2,4)}+c_{(3,5)}x_{(3,5)}+c_{(4,6)}x_{(4,6)}\)
\(=1+2+2+1+2=8\)
となり、これは上の全域木の重みの合計と一致します。今回は辺の重みが最小となる全域木を求めたいので、この目的関数を最小化することを考えます。
制約条件の設定
制約条件:
\(\sum\limits_{e \in E}x_e = |V|-1\)
\(\sum\limits_{e \in \delta(S)}x_e\geq 1 \;\;\; (\forall S \subset V, S \ne \emptyset)\)
\(x_e \in \{0,1\} \;\;\; (\forall e \in E)\)
3つ目の制約は変数が0か1しか取らないことを表しているだけなので説明は飛ばします。1つ目と2つ目の制約条件に付いてそれぞれ詳しく見ていきます。
この制約条件はグラフが木であるための条件である
グラフが
①連結である
②(頂点数-1)本の辺を持つ
ということを数式で表したものになります。
1つ目の制約条件
1つ目の制約条件:
\(\sum\limits_{e \in E}x_e = |V|-1\)
1つ目の制約条件は
採用する辺の本数は(頂点数-1)本
ということを表しています。
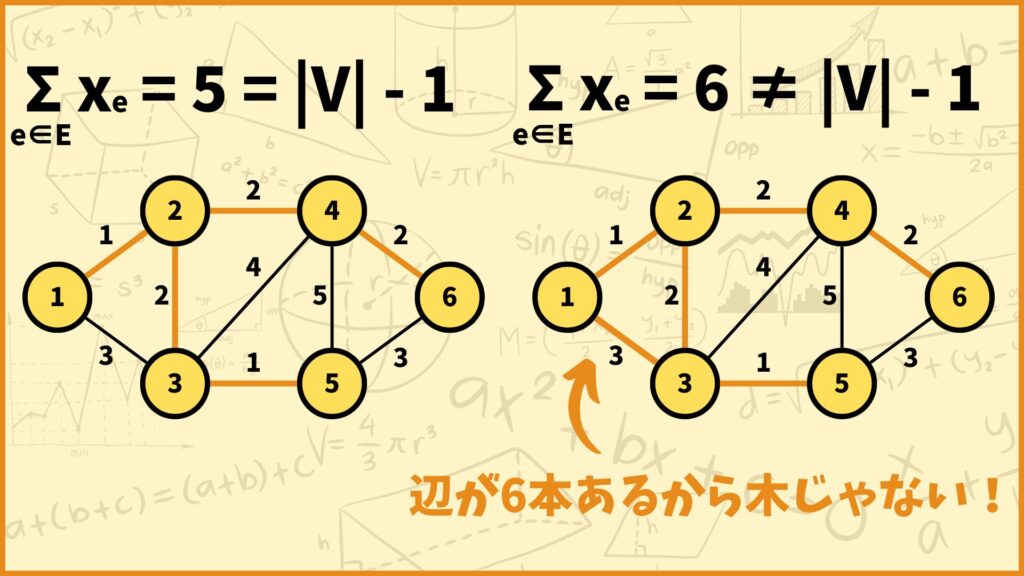
例えば上図の2つのグラフは6つの頂点を持つので、
\(|V|-1=6-1=5\)
となります。まず左側の例を見ると、5つの辺を採用していることが分かります。従って制約式の左辺は
\(\sum\limits_{e \in E}x_e = x_{(1,2)}+x_{(2,3)}+x_{(2,4)}+x_{(3,5)}+x_{(4,6)}=5\)
となり右辺の値と一致します。
それでは次に上図の右側の例を見ると6つの辺を採用していることが分かります。従って制約式の左辺は
\(\sum\limits_{e \in E}x_e = x_{(1,2)}+x_{(1,3)}+x_{(2,3)}+x_{(2,4)}+x_{(3,5)}+x_{(4,6)}=6\)
となり右辺の値と一致しません。
1つ目の制約条件は
②(頂点数-1)本の辺を持つ
ということを数式で表したものになります。
2つ目の制約条件
2つ目の制約条件:
\(\sum\limits_{e \in \delta(S)}x_e\geq 1 \;\;\; (\forall S \subset V, S \ne \emptyset)\)
\(\delta(S)\):頂点集合 \(S\) と \(V\backslash S\) つなぐ辺集合
2つ目の制約条件は
グラフが連結である
ということを表しています。
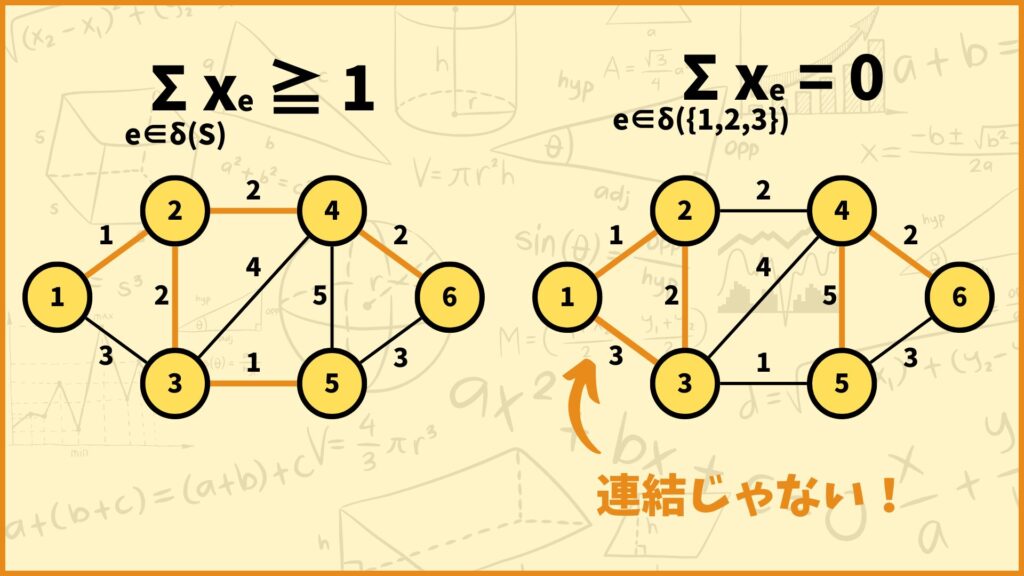
上図のグラフはどちらも5本の辺を持つので1つ目の制約条件を満たしています。ところがグラフを見てみると。左側は木ですが右側は木ではありません。なぜなら右側のグラフは2つ目の制約条件を満たしていないからです。
まず2つ目の制約条件に登場する \(\delta(S)\) について説明します。 \(\delta(S)\) は頂点集合 \(S\) と \(V\backslash S\) をつなぐ辺集合です。
例えば \(S = \{1,2,3\}\) とすると \(V\backslash S = \{4,5,6\}\) となります。このとき \(\{1,2,3\}\) と \(\{4,5,6\}\)をつなぐ辺は \((2,4), (3,5), (4,5)\) です。従って
\(\delta(\{1,2,3\}) = \{(2,4),(3,5),(4,5)\}\)
となります。これを踏まえて \(S=\{1,2,3\}\) の場合における2つ目の制約条件を考えてみましょう。まず左側のグラフについて制約式の左辺を考えると
\(\sum\limits_{e \in \delta(\{1,2,3\})}x_e=x_{(2,4)}+x_{(3,5)}+x_{4,5}=1+0+1=2\geq1\)
となり、制約式を満たしています。一方で右側のグラフについて考えてみると
\(\sum\limits_{e \in \delta(\{1,2,3\})}x_e=x_{(2,4)}+x_{(3,5)}+x_{4,5}=0+0+0=0<1\)
となり制約式を満たしていません。このように考えていくと、\(S = \{1,2,3\}\) 以外の頂点集合についても左側のグラフは2つ目の制約条件を満たしていることが分かります。
2つ目の制約条件は
①連結である
ということを数式で表したものになります。
最小全域木問題をpythonで解く
上のグラフの最小全域木を求めるコードは下の通りです。
## 必要なライブラリをインポート
import pulp
from itertools import combinations
## パラメータの設定
V = [1, 2, 3, 4, 5, 6] # 頂点集合
E = [(1, 2), (1, 3), (2, 3), (2, 4), (3, 4), (3, 5), (4, 5), (4, 6), (5, 6)] # 辺集合
c = {(1, 2) : 1,
(1, 3) : 3,
(2, 3) : 2,
(2, 4) : 2,
(3, 4) : 4,
(3, 5) : 1,
(4, 5) : 5,
(4, 6) : 2,
(5, 6) : 3} # 辺の重みの設定
# δ(S)を作成する関数を定義
def create_delta_S(S, E):
delta = [(i, j)
for (i, j) in E
if (i in S and j not in S)
or (i not in S and j in S)] # S と V\S を結ぶ辺を探す
return delta
## 整数計画問題として定式化
prob = pulp.LpProblem(sense = pulp.LpMinimize) # 問題を最小化に設定
x = pulp.LpVariable.dicts("x", E, cat="Binary") # 0-1変数の設定
prob += pulp.lpSum(c[e] * x[e] for e in E) # 目的関数
prob += pulp.lpSum(x[e] for e in E) == len(V) - 1 # 1つ目の制約
for r in range(1, len(V)):
for S in combinations(V, r):
delta_S = create_delta_S(S,E)
prob += pulp.lpSum(x[e] for e in delta_S) >= 1 # 2つ目の制約
prob.solve() # 問題を解く
## 結果の表示
print(f"解の状態 : {pulp.LpStatus[prob.status]}")
solution = [e for e in E if pulp.value(x[e]) == 1]
print("最適解 :")
for e in solution:
print(f"辺{e}")
このコードを実行すると上図の結果が得られました。
コードの解説
長いので1つずつ解説していきます。
必要なライブラリをインポート
## 必要なライブラリをインポート
import pulp
from itertools import combinations
ここではpulpとitertoolsからcombinationsをインポートしています。
pulpはpythonで整数計画問題を扱うのに使います。
combinationは頂点集合 \(V\) の部分集合 \(S\) を作成するために使います。
パラメータの設定
## パラメータの設定
V = [1, 2, 3, 4, 5, 6] # 頂点集合
E = [(1, 2), (1, 3), (2, 3), (2, 4), (3, 4), (3, 5), (4, 5), (4, 6), (5, 6)] # 辺集合
c = {(1, 2) : 1,
(1, 3) : 3,
(2, 3) : 2,
(2, 4) : 2,
(3, 4) : 4,
(3, 5) : 1,
(4, 5) : 5,
(4, 6) : 2,
(5, 6) : 3} # 辺の重みの設定
# δ(S)を作成する関数を定義
def create_delta_S(S, E):
delta = [(i, j)
for (i, j) in E
if (i in S and j not in S)
or (i not in S and j in S)] # S と V\S を結ぶ辺を探す
return delta
ここではパラメータを設定しています。
2行目では頂点集合 \(V\) をリストで設定しています。
3行目では辺集合 \(E\) をリストで設定しています。
4~12行目ではコスト \(c_e\) を辞書で設定しています。
14~20行目では \(\delta(S)\) を作成する関数を定義を設定しています。名前は「create_delta_S」で引数は頂点集合の部分集合「S」と辺集合「E」です。
「delta」に追加する辺「(i, j)」は(「S」中の頂点かつ「j」は「S」中の頂点じゃないもの)または(「S」中の頂点じゃないかつ「j」は「S」中の頂点であるもの)となります。
例えば「S = [1,2,3]」の場合、この関数に「S」と「E」を入力すると「(2,4), (3,4), (3,5)」が返されます。

整数計画問題として定式化
## 整数計画問題として定式化
prob = pulp.LpProblem(sense = pulp.LpMinimize) # 問題を最小化に設定
x = pulp.LpVariable.dicts("x", E, cat="Binary") # 0-1変数の設定
prob += pulp.lpSum(c[e] * x[e] for e in E) # 目的関数
prob += pulp.lpSum(x[e] for e in E) == len(V) - 1 # 1つ目の制約
for r in range(1, len(V)):
for S in combinations(V, r):
delta_S = create_delta_S(S,E)
prob += pul.lpSum(x[e] for e in delta_S) >= 1 # 2つ目の制約
prob.solve() # 問題を解く
ここでは整数計画問題として定式化しています。
2行目で問題を最小化に設定しています。引数の「sense」の所で最小化にするか最大化にするか決めることができます。
3行目で変数 \(x_e\) を設定しています。変数を設定する場合は「pulp.LpVariable」で設定できます。
引数は左から順に(名前, 添字の集合, 変数の種類)となっています。変数名は「x」、添字の集合は辺集合の「E」、変数の種類は0-1変数「Binary」としています。
4行目では目的関数を設定しています。\(\sum\)は「pulp.lpSum」で設定でき、括弧の中を「c[e] * x[e] for e in E」とすることで\(\sum\limits_{e \in E}c_ex_e\)を設定できます。
5行目では1つ目の制約の \(\sum\limits_{e \in E}x_e = |V|-1\) を設定しています。
6~9行目では2つ目の制約の \(\sum\limits_{e \in \delta(S)}x_e\geq 1 \; (\forall S \subset V, S \ne \emptyset)\) を設定しています。
「combination(V, r)」はリスト「V」中から「r」個の要素を選んだ時の選び方を列挙することができます。
例えば「V = [1,2,3,4,5]」、「r = 2」のときは「V」中の5個の要素から2個選んだ時の選び方を列挙するので、合計 \({}_5 C_2 = 10\) 個の要素を列挙します。

10行目では問題を解いています。
結果の表示
## 結果の表示
print(f"解の状態 : {pulp.LpStatus[prob.status]}")
solution = [e for e in E if pulp.value(x[e]) == 1]
print("最適解 :")
for e in solution:
print(f"辺{e}")
ここでは結果を表示しています。
2行目で解の状態を表示しています。「Optimal」と表示されたら最適解が得られています。
3~6行目で最適解を表示しています。

上図が出力結果ですがこれを見るとちゃんと最適解が得られており、最適解は辺 \((1,2),(2,3),(2,4),(3,5),(4,6)\) であることが分かります。
結果を図示する
最適解を表示することができましたが、文字だけだと分かりづらいので図示してみましょう。
# 必要なライブラリをインポート
import networkx as nx
import matplotlib.pyplot as plt
# 各ノードの座標を指定
pos = {
1: (0, 1),
2: (2, 1.5),
3: (2, 0.5),
4: (6, 1.5),
5: (6, 0.5),
6: (8, 1)
}
# グラフの作成
G = nx.Graph()
for (i, j) in E:
G.add_edge(i, j, weight=c[(i, j)])
# グラフの描画
nx.draw(G, pos, with_labels=True, node_color="orange", node_size=2000, font_size=16)
nx.draw_networkx_edge_labels(G, pos, edge_labels={(i, j): G[i][j]["weight"] for (i, j) in E}, font_size = 16)
# グラフを表示
plt.show()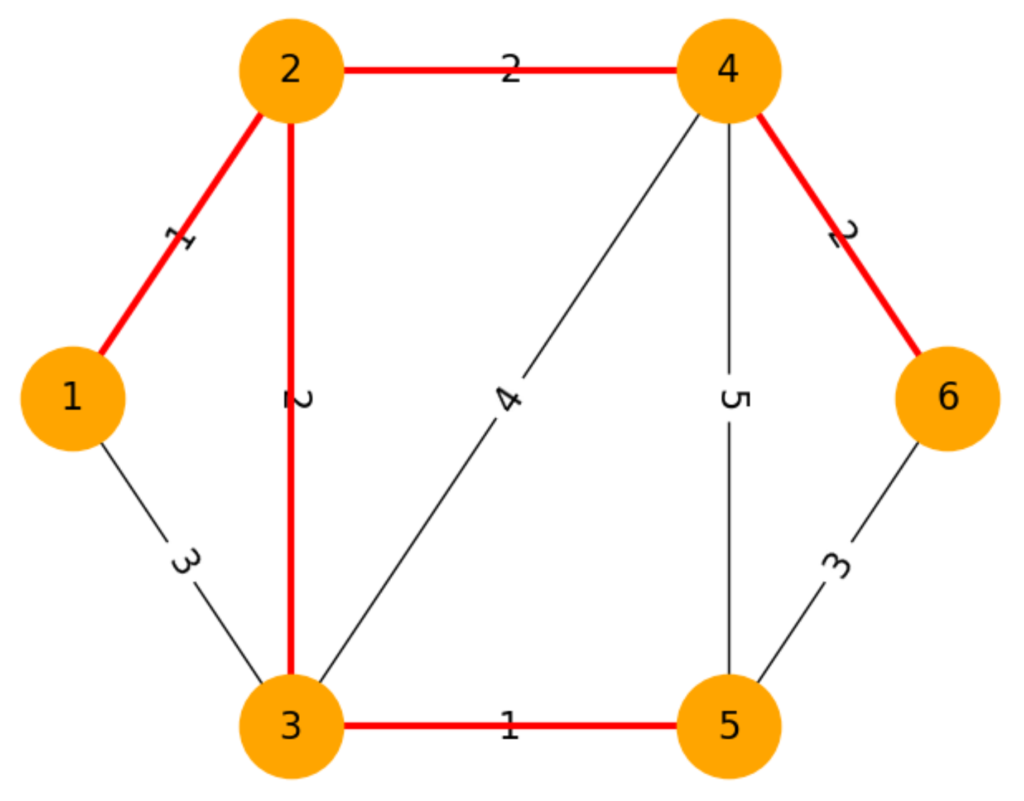
# 必要なライブラリをインポート
import networkx as nx
import matplotlib.pyplot as plt
# 各ノードの座標を指定
pos = {
1: (0, 1),
2: (2, 1.5),
3: (2, 0.5),
4: (6, 1.5),
5: (6, 0.5),
6: (8, 1)
}
# グラフの作成
G = nx.Graph()
for (i, j) in E:
G.add_edge(i, j, weight=c[(i, j)])
# グラフの描画
nx.draw(G, pos, with_labels=True, node_color="orange", node_size=2000, font_size=16)
nx.draw_networkx_edge_labels(G, pos, edge_labels={(i, j): G[i][j]["weight"] for (i, j) in E}, font_size = 16)
# 選ばれたエッジ(最小全域木のエッジ)を太線で強調表示
nx.draw_networkx_edges(G, pos, edgelist=solution, width=3, edge_color="red")
# グラフを表示
plt.show()
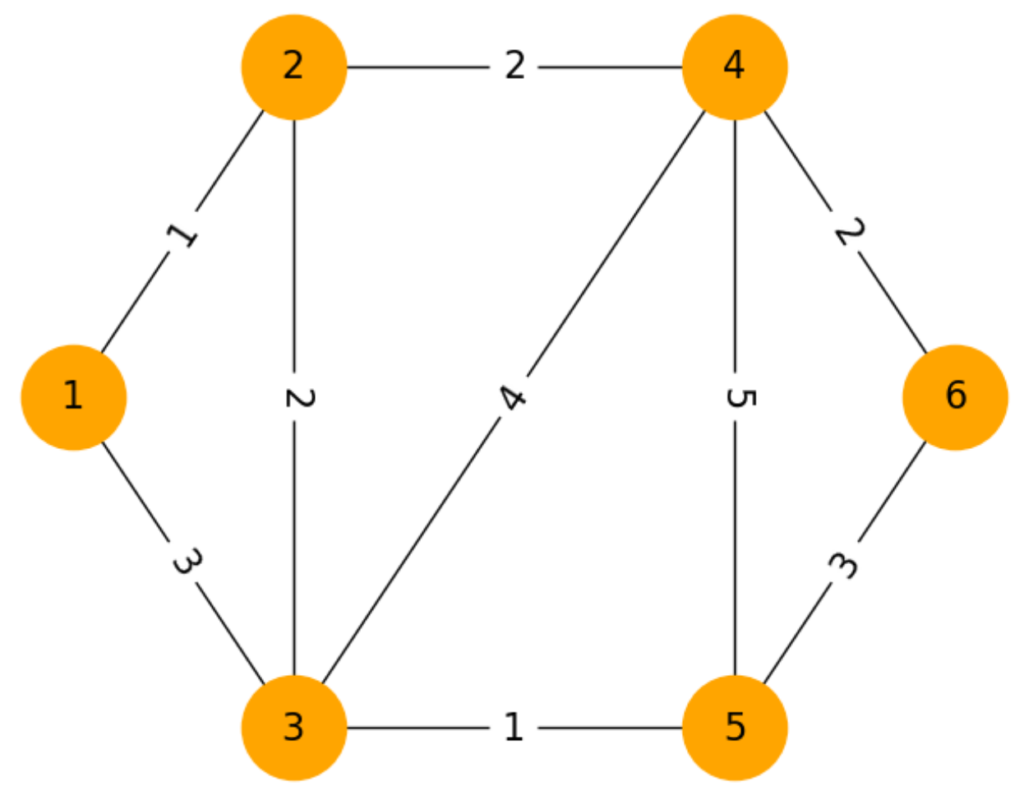
上のグラフはnetworkXとmatplotlibを使って描画しています。(本題ではないのでコードの説明は省略します。)
左側のグラフは今考えているグラフで、右側の赤線が最適解を表しています。こっちの方が最適解がどんな解なのか理解しやすいですね。
色々なグラフに対して問題を解いてみる
それでは最後に色々なグラフに対してこのコードを適用して最小全域木を求めてみましょう。
頂点数:8
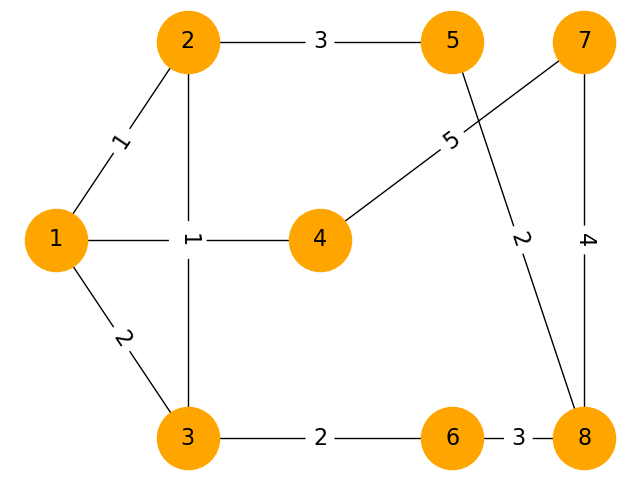
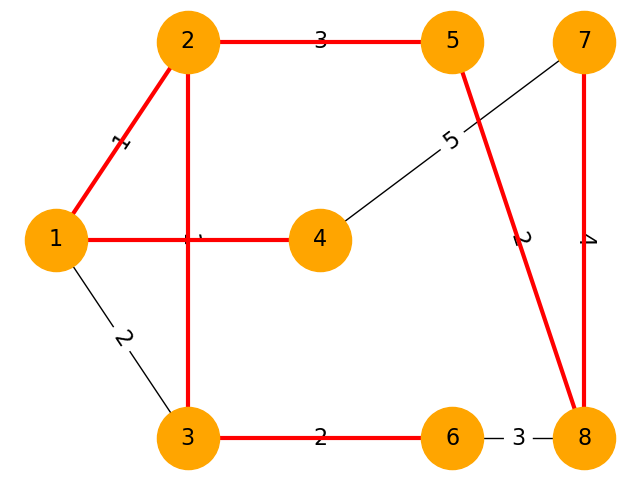
頂点数:10
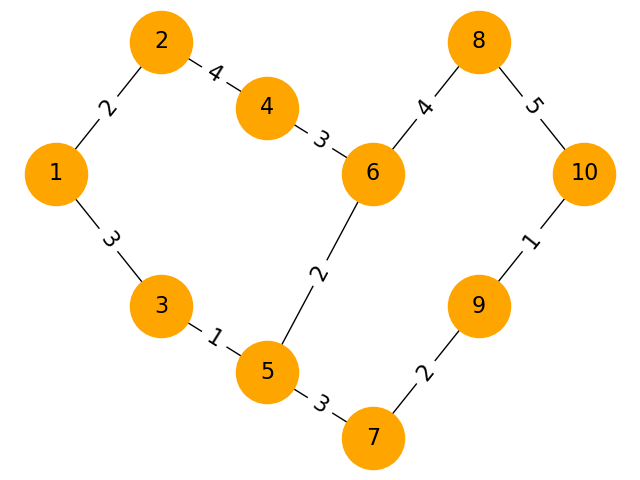
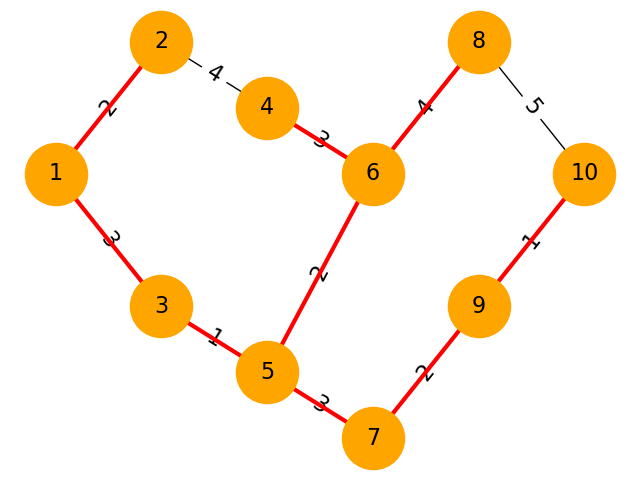
頂点数:15

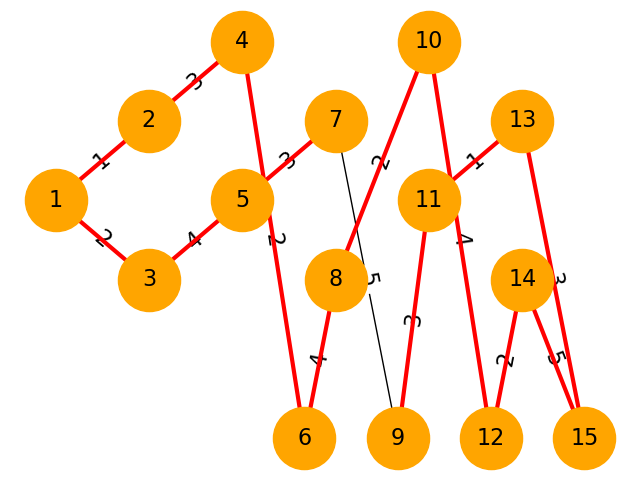
おわりに
いかがでしたか。
今回の記事では最小全域木問題について解説しました。
今後もこのような組合せ最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。
参考文献