- 焼きなまし法が遅い…
- 焼きなまし法をより高速にしたい…
- 実用的な焼きなまし法を実装したい…
こんにちは!しゅんです!
この記事は前回の記事の続きです。前回の記事を見てからこの記事を読む方が分かりやすいです!
\\ 前回の記事はこちら! //
それではやっていきましょう!
【Udemy講座公開のお知らせ】
このたびUdemyで数理最適化の講座を公開しました!この講座は「数理最適化を勉強してみたいけど数式が多くて難しい…」という方向けに、どうやって最適化問題を定式化すれば良いかを優しく丁寧に解説しています!
前回までのおさらい
まず最初に前回の記事でどんなことをしたのかを簡単に説明したいと思います。
割当問題を焼きなまし法で解いた
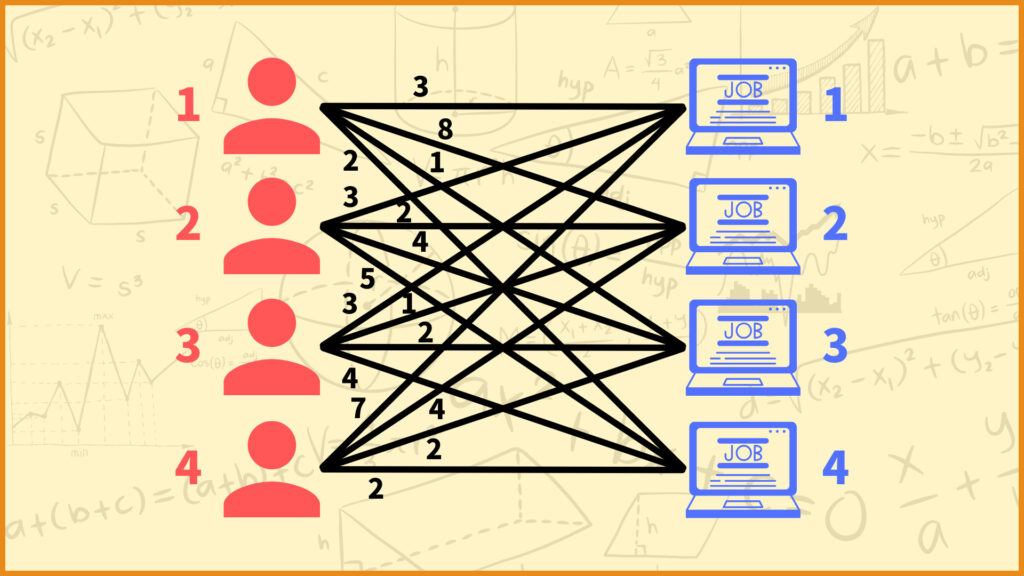
前回の記事では割当問題を焼きなまし法で解きました。例えば4人の従業員を4つの仕事に割り当てるときに、従業員の不満度が最小になるような割当を考えます。
また焼きなまし法では近傍解を考える必要があります。現在の解からちょっとだけ変更を加えた解を近傍解と言います。近傍解に作り方に関しては
近傍解の作り方:
現在の解からランダムに2つの仕事を選んで入れ替える
としました。例えば現在の解が
従業員1 ー 仕事3
従業員2 ー 仕事1
従業員3 ー 仕事4
従業員4 ー 仕事2
のとき、ランダムに2つの仕事を選んで入れ替えます。例えば仕事3と仕事4を入れ替えて得られる近傍解は
従業員1 ー 仕事4
従業員2 ー 仕事1
従業員3 ー 仕事3
従業員4 ー 仕事2
詳しい話は前回の記事で話しています。
\\ 前回の記事はこちら! //
割当問題を解く焼きなまし法をpythonで実装した
下のpythonコードによって割当問題を解く焼きなまし法を実装しました。
## 必要なライブラリをインポート
import numpy as np
import random
import copy
import math
np.random.seed(42)
## コストの合計を計算する関数を定義
def calculate_total_cost(cost_matrix, assignment):
total_cost = 0
for i, j in enumerate(assignment):
total_cost += cost_matrix[i][j]
return total_cost
## 近傍解を生成する関数を定義
def generate_neighbor(assignment):
neighbor = copy.deepcopy(assignment)
i, j = random.sample(assignment, 2)
neighbor[i], neighbor[j] = neighbor[j], neighbor[i]
return neighbor
## 焼きなまし法を実装する関数を定義
def simulated_annealing(cost_matrix, initial_temp, cooling_rate, max_iter):
# 初期解の生成(ランダムな割り当て)
current_assignment = list(range(len(cost_matrix)))
random.shuffle(current_assignment)
current_cost = calculate_total_cost(cost_matrix, current_assignment)
# 最良解の初期化
best_assignment = copy.deepcopy(current_assignment)
best_cost = current_cost
# 温度の初期化
temperature = initial_temp
# 最大反復回数(max_iter)まで繰り返し操作を行う
print("------------------------計算開始")
for iteration in range(max_iter):
neighbor = generate_neighbor(current_assignment) # generate_neighbor関数を使って近傍解の生成
neighbor_cost = calculate_total_cost(cost_matrix, neighbor) # calculate_total_cost関数を使って近傍解の目的関数値を計算
# 目的関数値の差の計算
delta_E = neighbor_cost - current_cost
# 解の受け入れ判定
if delta_E < 0:
# 目的関数値が改善された場合は受け入れる
current_assignment = neighbor
current_cost = neighbor_cost
# その時点での最良解より目的関数値が小さかったら再良解を更新
if neighbor_cost < best_cost:
best_assignment = neighbor
best_cost = neighbor_cost
else:
# 目的関数値が悪化した場合は確率的に受け入れる
acceptance_prob = math.exp(-delta_E / temperature) # 受け入れる確率を計算
if random.random() < acceptance_prob: # 0以上1以下のランダムに生成した実数が確率値より小さかったら解を受け入れる
current_assignment = neighbor
current_cost = neighbor_cost
# 温度の更新
temperature *= cooling_rate
# 終了条件(温度が十分低くなった場合)
if temperature < 1e-20:
break
# デバッグ用: 進捗表示
if iteration % 1000 == 0:
print(f"反復回数 {iteration}: 目的関数値 = {best_cost}")
print("------------------------計算終了")
return best_assignment, best_cost
## 問題例を入力して結果を出力する
# コスト行列を設定
n = 10 # 割当問題のサイズ
cost_matrix = np.random.randint(1, 11, size=(n, n)) # コスト行列を計算
# パラメータの設定
initial_temperature = 1000
cooling_rate = 0.995
max_iterations = 10001
# 焼きなまし法の実行
best_assignment, best_cost = simulated_annealing(cost_matrix, initial_temperature, cooling_rate, max_iterations)
# 結果の表示
print("最良の割り当て:", best_assignment)
print("目的関数値:", best_cost)
詳しい話は前回の記事で話しています。
\\ 前回の記事はこちら! //
前回のコードの問題点
ということで前回の記事では焼きなまし法で割当問題を解くpythonコードを紹介して終わったのですが、このコードには1つ問題点があります。それは
「近傍解の生成に時間がかかる」
「近傍解の評価に時間がかかる」
ということです。これについてもう少し詳しく見ていきましょう。
近傍解の生成に時間がかかる
まず前回のpythonコードの近傍解の生成方法をおさらいしていきます。「simulated_annealing」関数の36行目を見てみると
neighbor = generate_neighbor(current_assignment) # generate_neighbor関数を使って近傍解の生成「generate_neighbor」関数を使って近傍解を生成していることが分かります。「generate_neighbor」関数の中身を見てみると
## 近傍解を生成する関数を定義
def generate_neighbor(assignment):
neighbor = copy.deepcopy(assignment)
i, j = random.sample(assignment, 2)
neighbor[i], neighbor[j] = neighbor[j], neighbor[i]
return neighborという感じになっています。「assignment」は割当(1次元リスト)を表しています。例えば従業員数=仕事数=4で、「assignment = [3,1,4,2]」のときは
従業員1 – 仕事3
従業員2 – 仕事1
従業員3 – 仕事4
従業員4 – 仕事2
という割当を表します。
問題なのは
neighbor = copy.deepcopy(assignment)の部分です。まず「assignment」は1次元リストなので「deepcopy」を使う必要はないです。なぜ当時の自分は「deepcopy」を使っていたのか謎です。
ということでただの「copy」を使ってみます。
## 近傍解を生成する関数を定義
def generate_neighbor(assignment):
neighbor = assignment.copy()
i, j = random.sample(assignment, 2)
neighbor[i], neighbor[j] = neighbor[j], neighbor[i]
return neighborで次に、今のコードは「generate_neighbor」関数を呼び出すたびに「copy」を実施しています。「copy」の計算量は\(O(n)\)なので、これだと計算時間がかなりかかってしまいます。
「copy」を実行するのは最良解を更新するときだけで良いので、近傍解を生成するたびに「copy」を使う必要はないですね。
近傍解の評価に時間がかかる
次に前回のpythonコードの近傍解の評価方法をおさらいしていきます。「simulated_annealing」関数の36~39行目を見てみると
neighbor = generate_neighbor(current_assignment) # generate_neighbor関数を使って近傍解の生成
neighbor_cost = calculate_total_cost(cost_matrix, neighbor) # calculate_total_cost関数を使って近傍解の目的関数値を計算
# 目的関数値の差の計算
delta_E = neighbor_cost - current_costとなっています。簡単な流れを説明すると
- STEP 1:「generate_neighbor」関数で近傍解を生成する
- STEP 2:「calculate_total_cost」関数で近傍解の目的関数値を計算する
- STEP 3:「neighbor_cost」(近傍解の目的関数値)から「current_cost」(最良解の目的関数値)を引き算して目的関数値が改善されたか調べる
という感じです。STEP 1で登場する「generate_neighbor」関数は今さっき説明しました。しかしまだ問題があります。それは「calculate_total_cost」関数です。
「calculate_total_cost」関数の中身を見てみると下のコードのようになっています。
## コストの合計を計算する関数を定義
def calculate_total_cost(cost_matrix, assignment):
total_cost = 0
for i, j in enumerate(assignment):
total_cost += cost_matrix[i][j]
return total_cost「cost_matrix」がコスト行列、「assignment」が割当を表しています。例えば従業員数=仕事数=4で、「assignment = [3,1,4,2]」を考えます。これは
従業員1 – 仕事3
従業員2 – 仕事1
従業員3 – 仕事4
従業員4 – 仕事2
という割当を表します。そのため上のコードの
for i, j in enumerate(assignment):
total_cost += cost_matrix[i][j]という部分はfor文で4回足し算を行っていることになります。
より一般的に考えると\(n\)人の従業員を\(n\)個の仕事に割り当てるとき、「neighbor_cost」を計算するためにかかる計算量は\(O(n)\)となります。
これだと時間がかかってしまいます。何とかこの部分を\(O(1)\)で評価できないかを考えます。
どうやって近傍解の評価にかかる計算量を少なくするの?
それではどうやって近傍解の評価にかかる計算量を\(O(1)\)に減らすのかを考えていきます。
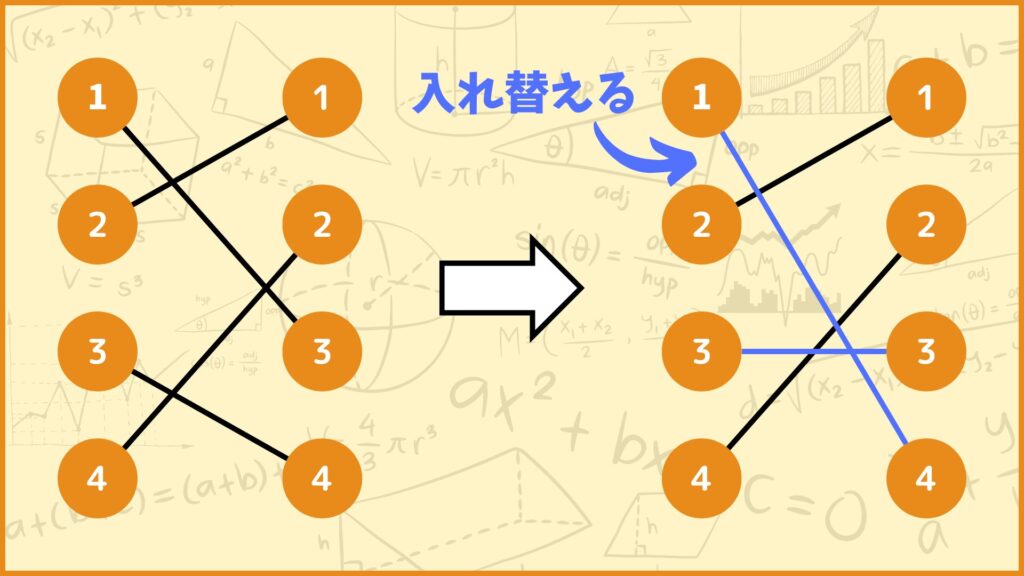
上図のように近傍解を生成したとします。元々は1-3、3-4という割当だったんですけど、ここを入れ替えて1-4、3-3という近傍解を作成しました。このときコストを\(c_{ij}\)とすると、今の解と近傍解の目的関数値の差は
\((c_{14}+c_{21}+c_{33}+c_{42})-(c_{13}+c_{21}+c_{34}+c_{42})\)
\(=(c_{14}+c_{33})-(c_{13}+c_{34})\)
と計算できます。ここでポイントなのは
入れ替えてないペアのコストは考えなくてよい
ということです。例えば2-1というペアは今の解にも近傍解にもありますね。計算式を見てみると\(c_{21}\)は左側にも右側にも登場しているので結果的に足し引き0になります。
そう考えると、今の解と近傍解の目的関数値の差は近傍解を作成する際に入れ替えた2ペアだけを考えればOKです。
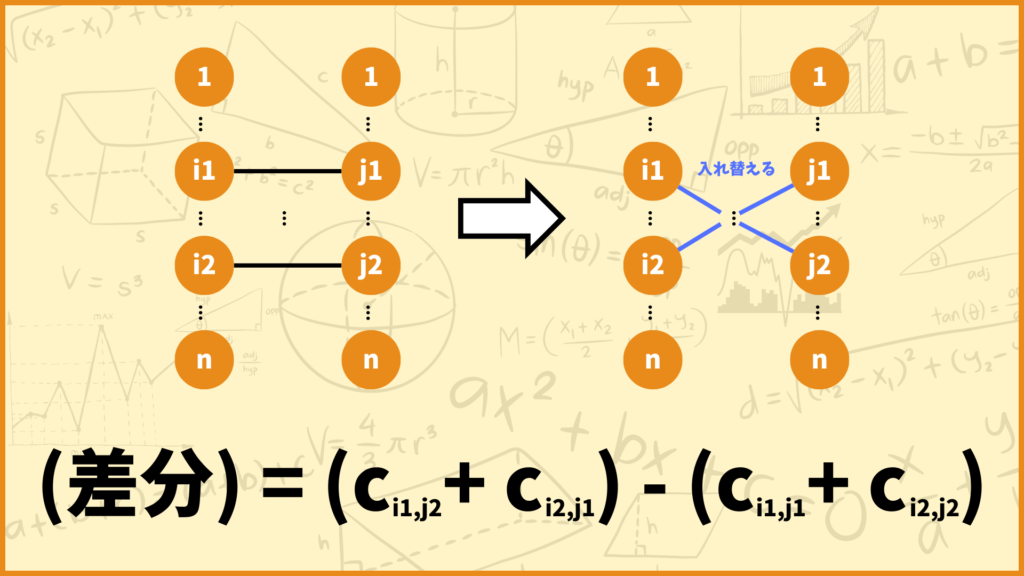
より一般的に考えてみます。今の解の \(i_1-j_1,\; i_2-j_2\) を \(i_1-j_2,\; i_2-j_1\) に入れ替えたものを近傍解とします。このとき今の解と近傍解の目的関数値の差は
\((c_{i_1,j_2}+c_{i_2,j_1})-(c_{i_1,j_1}+c_{i_2,j_2})\)
と計算できます。\(n=100\)でも\(n=1000\)でも\(n=10000\)でも上の式で差分を計算することができます。従ってこの計算式を使えば近傍解の評価を\(O(1)\)で行うことができます。
pythonで改良版焼きなまし法を実装する
それではここまで話してきたことをpythonで実装していきましょう。
## 必要なライブラリをインポート
import numpy as np
import random
import copy
import math # mathモジュールの追加
np.random.seed(42)
## コストの合計を計算する関数を定義
def calculate_total_cost(cost_matrix, assignment):
total_cost = 0
for i, j in enumerate(assignment):
total_cost += cost_matrix[i][j]
return total_cost
## 焼きなまし法を実装する関数を定義
def simulated_annealing(cost_matrix, initial_temp, cooling_rate, max_iter):
# 初期解
current_assignment = list(range(len(cost_matrix)))
random.shuffle(current_assignment)
current_cost = calculate_total_cost(cost_matrix, current_assignment)
# 最良解
best_assignment = current_assignment.copy() # 一度だけコピー
best_cost = current_cost
temperature = initial_temp
for iteration in range(max_iter):
# 交換する2つの位置を選択するだけ(コピーなし)
i1, i2 = random.sample(range(len(current_assignment)), 2)
# 現在の割り当て値
j1 = current_assignment[i1]
j2 = current_assignment[i2]
# コスト差分の計算
delta_E = (cost_matrix[i1][j2] + cost_matrix[i2][j1]) - (cost_matrix[i1][j1] + cost_matrix[i2][j2])
# 解の受け入れ判定
if delta_E < 0 or random.random() < math.exp(-delta_E / temperature):
# 受け入れる場合は現在の解を実際に変更
current_assignment[i1], current_assignment[i2] = current_assignment[i2], current_assignment[i1]
current_cost += delta_E
# 最良解の更新
if current_cost < best_cost:
best_assignment = current_assignment.copy() # 最良解の時だけコピー
best_cost = current_cost
# 温度の更新
temperature *= cooling_rate
# 終了条件(温度が十分低くなった場合)
if temperature < 1e-20:
break
# デバッグ用: 進捗表示
if iteration % 1000 == 0:
print(f"反復回数 {iteration}: 目的関数値 = {best_cost}")
print("------------------------計算終了")
return best_assignment, best_cost
## 問題例を入力して結果を出力する
# コスト行列を設定
n = 10 # 割当問題のサイズ
cost_matrix = np.random.randint(1, 11, size=(n, n)) # コスト行列を計算
# パラメータの設定
initial_temperature = 1000
cooling_rate = 0.995
max_iterations = 10001
# 焼きなまし法の実行
best_assignment, best_cost = simulated_annealing(cost_matrix, initial_temperature, cooling_rate, max_iterations)
# 結果の表示
print("最良の割り当て:", best_assignment)
print("目的関数値:", best_cost)
大きく変更したところは2つあります。1つは近傍解生成を行う「generate_neighbor」関数を削除し、「simulated_annealing」関数内部で近傍解の生成及び最良解の更新を行っています。
2つ目は近傍解の評価をするときに毎回「calculate_total_cost」関数を使っていたのを止めて、\(O(1)\)の計算で解の評価を行っています。
どれくらい計算時間が短くなったか実験してみる
それでは最後に改良前と改良後でどれくらい計算時間が短くなったのか簡単に実験してみましょう。実験の設定は下記のようにします。
・\(n=10,100,1000,10000\) の4パターンで実験する。
・「np.random.seed(42)」でシード値を固定し、改良前と改良後で同じ問題を1回ずつ解く。
・コスト \(c_{ij}\) は \(1\leq c_{ij}\leq n\) を満たす任意の自然数を取りうる。
なお計算環境は下記の通りである。
プロセッサ:Intel(R) Core(TM) i5-1035G7 CPU @ 1.20GHz 1.50 GHz
実装RAM:16.0 GB
| 問題サイズ | 改良前(秒) | 改良後(秒) | 何倍速くなったか |
|---|---|---|---|
| \(n=10\) | 0.34 | 0.10 | 3.4倍 |
| \(n=100\) | 1.64 | 0.14 | 11.7倍 |
| \(n=1000\) | 13.38 | 0.28 | 47.8倍 |
| \(n=10000\) | 210.54 | 0.38 | 554.1倍 |
ということで計算結果を上の表にまとめました。違いがはっきりと表れていますね。改良前は \(n=10000\) で210秒程度かかっていますが、改良後はたった0.38秒と554倍速く計算することができました。
おわりに
今回は焼きなまし法のロジックを改良して計算時間を短くしてみました!
今後もこのような組合せ最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。





