こんにちは!しゅんです!
割当問題を簡単に説明すると、例えば10人の従業員を10個の仕事に割り当てるときにどのように割り当てたら効率的になるかを考える問題です。
今回の記事では割当問題の中でも
「時間帯によって異なる仕事を行う場合の割当問題」
を整数計画問題として定式化してみたいと思います。それではやっていきましょう!
「従業員に余りが出る場合の割当問題」
「従業員が複数の仕事を担当できる場合の割当問題」
「時間帯によって異なる仕事を行う場合の割当問題」
「1日でやる仕事数に上限がある場合の割当問題」
「最も負担がかかる従業員の負担を最小にする割当問題」
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
具体例を使って考える
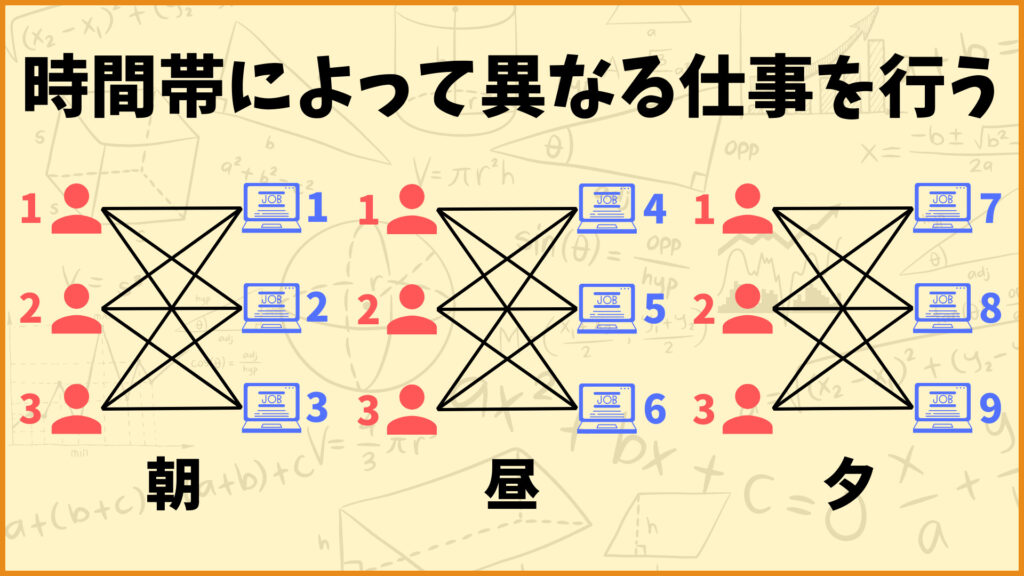
今回は3人の従業員に9個の仕事を割り当てることを考えます。9個の仕事は朝、昼、夕の3つの時間帯で分けられていて、朝に仕事1,2,3、昼に仕事4,5,6、夕に仕事7,8,9を行います。
各時間帯において各従業員は必ず1つの仕事が割り当てられ、各仕事は必ず1人の従業員に割り当てられます。各辺には重みがあります。ごちゃごちゃするので図では省略しています。
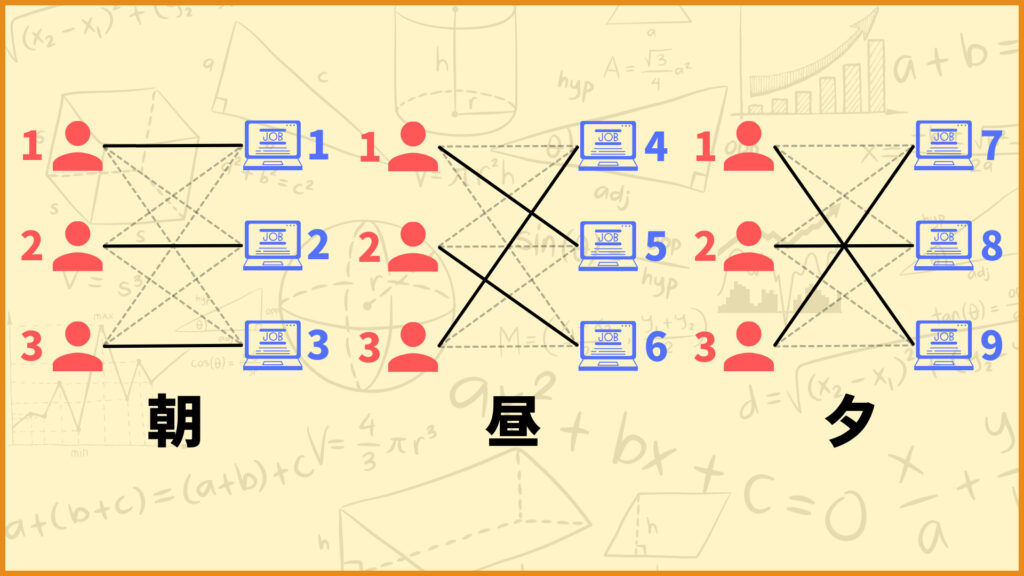
上図の例で言うと、朝は「従業員1が仕事1、従業員2が仕事2、従業員3が仕事3」を担当し、昼は「従業員1が仕事5、従業員2が仕事6、従業員3が仕事4」を担当し、夕は「従業員1が仕事9、従業員2が仕事8、従業員3が仕事7」を担当します。
今回はこのような割当の中で、重みの合計が最小となるような割当を求める問題を整数計画問題として定式化してみたいと思います。
整数計画問題として定式化する
「変数・パラメータ」、「目的関数」、「制約条件」の順番で説明したいと思います。
変数・パラメータの設定
パラメータとして時間帯の集合\(T\)、従業員の集合\(E\)、仕事の集合\(J_1,J_2,J_3\)、辺\((i,j)\)の重み\(w_{ij}\)を設定します。(朝を1、昼を2、夕を3とします。)
オーソドックスな割当問題と違って今回は時間帯という概念を追加するので、仕事の集合も朝、昼、夕の3つに分けます。
また0-1変数として\(x_{ijt}\)を設定します。この変数\(x_{ijt}\)は時間帯\(t\)に従業員\(i\)に仕事\(j\)が割り当てられれば1、そうでなければ0を取ります。
・パラメータ
\(T = \{1,2,3\}\):時間帯の集合
\(E = \{1,2,3\}\) : 従業員の集合
\(J_1 = \{1,2,3\}\) : 朝の仕事の集合
\(J_2 = \{4,5,6\}\) : 昼の仕事の集合
\(J_3 = \{7,8,9\}\) : 夕の仕事の集合
\(w_{ij}\) : 辺\((i,j)\)の重み
・変数
\(x_{ijt} \in \{0,1\} \;\; (\forall t \in T, \forall i \in E, \forall j \in J_t)\)
目的関数の設定
目的関数は以下のように設定できます。
\(\sum\limits_{t \in T}\sum\limits_{i \in E}\sum\limits_{j \in J_t} w_{ij}x_{ijt}\)
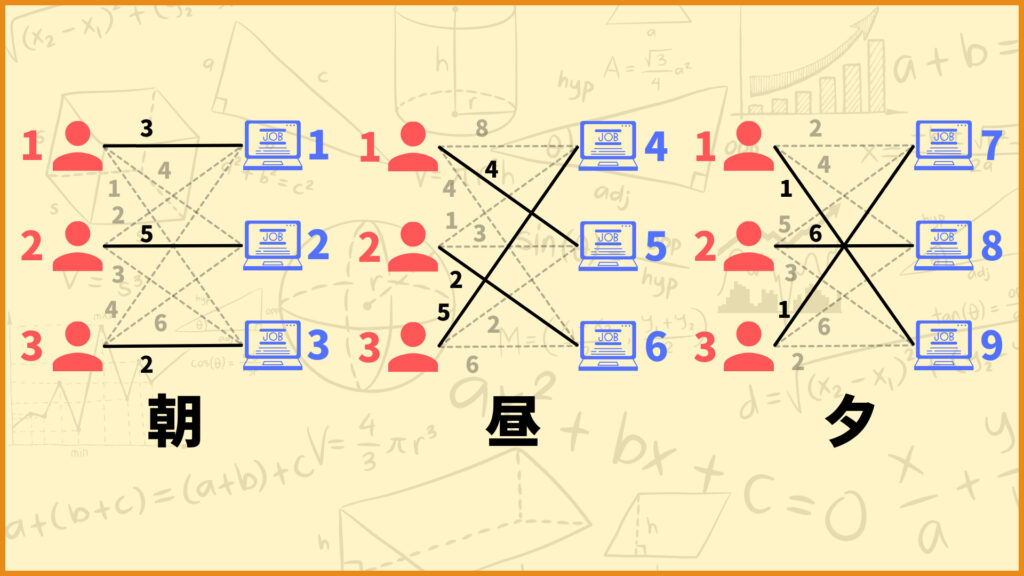
例えば上図の左側の例だと、朝\((t=1)\)は\(x_{131},x_{221},x_{331}\)が1、昼\((t=2)\)は\(x_{152},x_{262},x_{342}\)が1、夕\((t=3)\)は\(x_{193},x_{283},x_{373}\)が1でそれ以外が0となります。
したがって\(\sum\limits_{t \in T}\sum\limits_{i \in E}\sum\limits_{j \in J_t} w_{ij}x_{ijt}\)の値は
\(\sum\limits_{t \in T}\sum\limits_{i \in E}\sum\limits_{j \in J_t} w_{ij}x_{ijt}\)
\( = w_{11}x_{111} + w_{12}x_{121} + w_{13}x_{131}\)
\( + w_{21}x_{211} + w_{22}x_{221} + w_{23}x_{231}\)
\( + w_{31}x_{311} + w_{32}x_{321} + w_{33}x_{331}\)
\( + w_{14}x_{142} + w_{15}x_{152} + w_{16}x_{162}\)
\( + w_{24}x_{242} + w_{25}x_{252} + w_{26}x_{262}\)
\( + w_{34}x_{342} + w_{35}x_{352} + w_{36}x_{362}\)
\( + w_{17}x_{173} + w_{18}x_{183} + w_{19}x_{193}\)
\( + w_{27}x_{273} + w_{28}x_{283} + w_{29}x_{293}\)
\( + w_{37}x_{373} + w_{38}x_{383} + w_{39}x_{393}\)
\(= (3 \times 1) + (4 \times 0) + (1 \times 0)\)
\(+ (2 \times 0) + (5 \times 1) + (3 \times 0)\)
\(+ (4 \times 0) + (6 \times 0) + (2 \times 1)\)
\(+ (8 \times 0) + (4 \times 1) + (4 \times 0)\)
\(+ (1 \times 0) + (3 \times 0) + (2 \times 1)\)
\(+ (5 \times 1) + (2 \times 0) + (6 \times 0)\)
\(+ (2 \times 0) + (4 \times 0) + (1 \times 1)\)
\(+ (5 \times 0) + (6 \times 1) + (3 \times 0)\)
\(+ (1 \times 1) + (6 \times 0) + (2 \times 0)\)
\(= 3 + 5 + 2 + 4 + 2 + 5 + 1 + 6 + 1 = 29\)
となります。
制約条件の設定
最後に制約条件について設定したいと思います。従業員側の制約条件と仕事側の制約条件に分けて説明したいと思います。
従業員側の制約条件
従業員側の制約条件は以下のように設定できます。
\( \sum\limits_{j \in J_t} x_{ijt} = 1 \;\;\; (\forall t \in T, \forall i \in E)\)
例えば朝\((t=1)\)の従業員1について考えてみましょう。従業員1は仕事1~3のどれかを必ず1つ担当します。
これを制約条件で言い換えましょう。
\(x_{111} = 1\)となるパターン
\(x_{121} = 1\)となるパターン
\(x_{131} = 1\)となるパターン
の3パターンだったらOKっていう制約条件を作ります。これは
\(x_{111} + x_{121} + x_{131} = 1\)
という制約式で表現することができます。\(\sum\)を使ってこの式表すと
\(\sum\limits_{j \in J_1} x_{1j} = 1 \)
となります。この制約式を\(t = 2,3, i = 2,3\)に対しても作れば全ての時間帯の全ての従業員に対して制約条件を作ることができます。
仕事側の制約条件
仕事側の制約条件は以下のように設定できます。
\( \sum\limits_{i \in E} x_{ijt} = 1 \;\;\; (\forall t \in T, \forall j \in J_t)\)
例えば朝\((t=1)\)の仕事1について考えてみましょう。仕事1は従業員1~3のうちだれか1人に割り当てられます。
これを制約条件で言い換えると
\(x_{111} = 1\)のパターン
\(x_{211} = 1\)のパターン
\(x_{311} = 1\)のパターン
の3つだったらOKっていう制約条件を作ります。これは
\(x_{111} + x_{211} + x_{311} = 1\)
という制約式で表現することができます。\(\sum\)を使ってこの式表すと
\(\sum\limits_{i \in E} x_{i11} = 1 \)
となります。この制約式を\(j = 2,3,…,9\)に対しても作れば全ての仕事に対して制約条件を作ることができます。
\(t=1\)とすれば\(J_t = \{1,2,3\}\)となり、仕事1,2,3を指定できます。
\(t=2\)とすれば\(J_t = \{4,5,6\}\)となり、仕事4,5,6を指定できます。
\(t=3\)とすれば\(J_t = \{7,8,9\}\)となり、仕事7,8,9を指定できます。
このように時間帯\(t\)を動かすと仕事の集合\(J_t\)が自動的に決まり、その結果仕事1,2,…,9を指定することができます。
整数計画問題としてまとめる
最後にこれらをまとめて整数計画問題として定式化しましょう。
定式化:
\(\min \;\;\; \sum\limits_{t \in T}\sum\limits_{i \in E}\sum\limits_{j \in J_t} w_{ij}x_{ijt}\)
\(\;\text{s.t.}\;\;\;\sum\limits_{j \in J_t} x_{ijt} = 1 \;\;\;\; (\forall t \in T, \forall i \in E)\)
\(\;\;\;\;\;\;\;\;\;\;\sum\limits_{i \in E} x_{ijt}=1 \;\;\;\; (\forall t \in T, \forall j \in J_t)\)
\(\;\;\;\;\;\;\;\;\; x_{ijt} \in \{0,1\} \;\;(\forall t \in T, \forall i \in E, \forall j \in J_t)\)
次回の記事では今回定式化した整数計画問題をpythonで表現して実際に問題を解いてみたいと思います!
次回の記事はこちらから!
現在制作中
おわりに
いかがでしたか。
今回の記事では割当問題について解説していきました。
今後もこのような数理最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。







