こんにちは!しゅんです!
この記事では具体例を使って線形緩和した最小頂点被覆問題の双対問題を求めます。
前回の記事で最小頂点被覆問題を整数計画問題として定式化する方法を解説しました。
前回の記事はこちらから!
それではやっていきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
最大頂点被覆問題を整数計画問題として定式化して線形緩和する
それではまず最小頂点被覆問題を整数計画問題として定式化して線形緩和してみましょう。
整数計画問題として定式化する
パラメータ:
\(V\) : 頂点集合
\(E\) : 辺集合
\(c_{i}\) : 頂点\(i\)のコスト
変数:
\(x_{i} \in \{0,1\}\) : 頂点\(i\)を選ぶなら1、選ばないなら0を取る0-1変数
定式化:
\( \min \;\;\; \sum\limits_{i \in V}c_{i}x_{i}\)
\(\;\text{s.t.}\;\;\;x_{i} + x_{j} \geq 1 \;\;\; (\forall (i,j) \in E)\)
\(\;\;\;\;\;\;\;\;\; x_{i} \in \{0,1\} \;\;\; (\forall i \in V)\)
最小頂点被覆問題を整数計画問題として定式化しました。定式化の方法は前回の記事で説明しているのでここでは飛ばします。
今回は各頂点のコストを全て1とします。つまり任意の頂点\(i\)に対して\(c_i = 1\)の場合を考えていきます。
パラメータ:
\(V\) : 頂点集合
\(E\) : 辺集合
\(c_{i}\) : 頂点\(i\)のコスト
変数:
\(x_{i} \in \{0,1\}\) : 頂点\(i\)を選ぶなら1、選ばないなら0を取る0-1変数
定式化:
\( \min \;\;\; \sum\limits_{i \in V}x_{i}\)
\(\;\text{s.t.}\;\;\;x_{i} + x_{j} \geq 1 \;\;\; (\forall (i,j) \in E)\)
\(\;\;\;\;\;\;\;\;\; x_{i} \in \{0,1\} \;\;\; (\forall i \in V)\)
線形緩和する
パラメータ:
\(V\) : 頂点集合
\(E\) : 辺集合
\(c_{i}\) : 頂点\(i\)のコスト
変数:
\(x_{i} \in \{0,1\}\) : 頂点\(i\)を選ぶなら1、選ばないなら0を取る0-1変数
定式化:
\( \min \;\;\; \sum\limits_{i \in V}x_{i}\)
\(\;\text{s.t.}\;\;\;x_{i} + x_{j} \geq 1 \;\;\; (\forall (i,j) \in E)\)
\(\;\;\;\;\;\;\;\;\; x_{i} \geq 0 \;\;\; (\forall i \in V)\)
さっきの整数計画問題を線形緩和しました。線形緩和とは0-1変数を0以上1以下にすることです。今回の例だと
\(x_i \in \{0,1\} \rightarrow 0 \leq x_i \leq 1\)
とします。ただ\(x_i \leq 1\)という部分は必要ないです。なぜなら仮にある実行可能解の中に\(x_i >1\)となる変数\(x_i\)があった場合、その変数を\(x_i = 1\)とすれば目的関数値がより小さい実行可能解が得られるためです。
そのため今回の場合線形緩和したときの変数に関する制約は
\(x_i \in \{0,1\} \rightarrow x_i \geq 0\)
と表すことができます。以降「最小頂点被覆問題を線形計画問題として定式化する」と言ったら上記の定式化をすると考えてください。
一般に上記の線形計画問題の最適解は整数解であるとは限りません。一方でグラフが2部グラフの場合、線形緩和した問題の最適解で整数解のものが存在します。
詳しい話はこちらの記事で解説しています!
現在制作中
具体例を使って双対問題を考えてみる
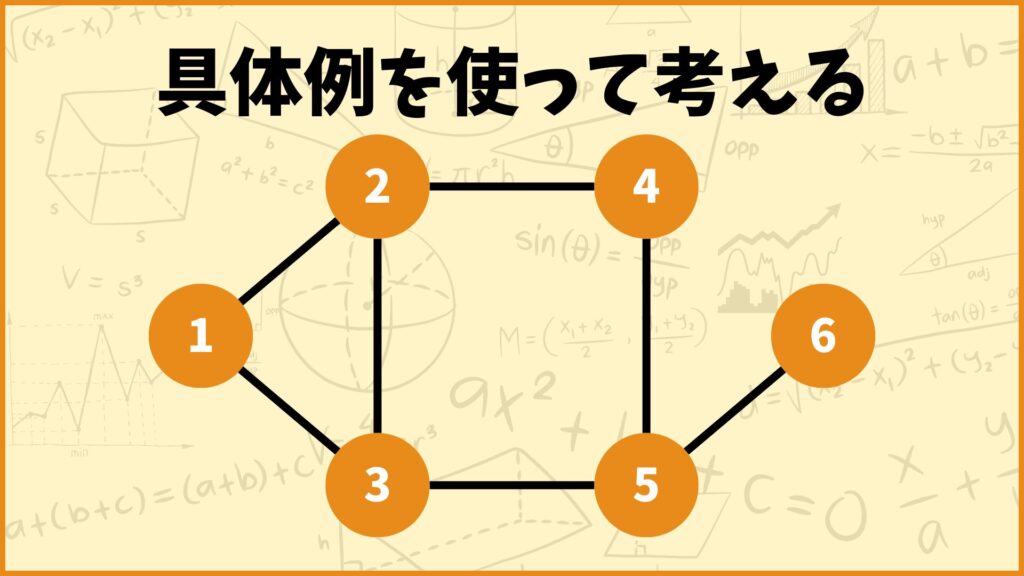
上のグラフを使って双対問題を考えていきたいと思います。
線形計画問題として定式化
まず最初に上記のグラフにおける最小頂点被覆問題を線形計画問題として定式化しましょう。分かりやすくするために\(\sum\)を使わずに記述してみます。
頂点集合\(V\)と辺集合\(E\)は以下のようになります。
\(V = \{1,2,3,4,5,6\}\)
\(E = \{(1,2),(1,3),(2,3),(2,4),(3,5),(4,5),(5,6)\}\)
目的関数は以下のように表せます。
\(x_{1} + x_{2} + x_{3} + x_{4}+ x_{5} + x_{6}\)
制約条件は以下のように表せます。
\(x_{1}+x_{2} \geq 1\) ・・・ 辺\((1,2)\)に関する制約
\(x_{1}+x_{3} \geq 1\) ・・・ 辺\((1,3)\)に関する制約
\(x_{2}+x_{3} \geq 1\) ・・・ 辺\((2,3)\)に関する制約
\(x_{2}+x_{4} \geq 1\) ・・・ 辺\((2,4)\)に関する制約
\(x_{3}+x_{5} \geq 1\) ・・・ 辺\((3,5)\)に関する制約
\(x_{4}+x_{5} \geq 1\) ・・・ 辺\((4,5)\)に関する制約
\(x_{5}+x_{6} \geq 1\) ・・・ 辺\((5,6)\)に関する制約
後は変数の非負制約が存在するので、まとめると上の具体例における最小頂点被覆問題を線形計画問題として定式化すると以下のようになります。
目的関数(最小化):
\(x_{1} + x_{2} + x_{3} + x_{4}+ x_{5} + x_{6}\)
制約条件:
\(x_{1}+x_{2} \geq 1\)
\(x_{1}+x_{3} \geq 1\)
\(x_{2}+x_{3} \geq 1\)
\(x_{2}+x_{4} \geq 1\)
\(x_{3}+x_{5} \geq 1\)
\(x_{4}+x_{5} \geq 1\)
\(x_{5}+x_{6} \geq 1\)
\(x_1,x_2,x_3,x_4,x_5,x_6 \geq 0\)
行列・ベクトルを使って表記する
主問題:
\(\min \;\;\; c^\top x\)
\(\;\text{s.t.}\;\;\;Ax \leq b \)
\(\;\;\;\;\;\;\;\;\; x \geq 0\)
双対問題:
\(\max \;\;\; b^\top y\)
\(\;\text{s.t.}\;\;\;A^\top y \geq c \)
\(\;\;\;\;\;\;\;\;\; y\geq 0\)
上の主問題とその双対問題は上記のような関係です。行列、ベクトルを使って表されているので今回の目的関数、制約条件も行列、ベクトルを使って表しましょう。
まず目的関数は以下のように表せます。
\(\begin{pmatrix}1&1&1&1&1&1\end{pmatrix} \begin{pmatrix}x_{1}\\x_{2}\\x_{3}\\x_{4}\\x_{5}\\x_{5}\end{pmatrix}\)
よって\(c,x\)を下のようにすれば上の主問題の形と合わせられます。
\(c=\begin{pmatrix}1\\1\\1\\1\\1\\1\end{pmatrix}, x=\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\\x_{4}\\x_{5}\\x_{6}\end{pmatrix}\)
次に制約条件を行列、ベクトルを使って表すと以下のようになります。
\(\begin{pmatrix}1&1&0&0&0&0\\1&0&1&0&0&0\\0&1&1&0&0&0\\0&1&0&1&0&0\\0&0&1&0&1&0\\0&0&0&1&1&0\\0&0&0&0&1&1\end{pmatrix}\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\\x_{4}\\x_{5}\\x_{6}\end{pmatrix} = \begin{pmatrix}1\\1\\1\\1\\1\\1\\1\end{pmatrix}\)
よって\(A,b\)を下のようにすれば上の主問題の形と合わせられます。
\(A = \begin{pmatrix}1&1&0&0&0&0\\1&0&1&0&0&0\\0&1&1&0&0&0\\0&1&0&1&0&0\\0&0&1&0&1&0\\0&0&0&1&1&0\\0&0&0&0&1&1\end{pmatrix} , b= \begin{pmatrix}1\\1\\1\\1\\1\\1\\1\end{pmatrix}\)
よく見ると\(A\)がグラフの接続行列の転置行列になっていることが分かります。
接続行列はこちらの記事で詳しく解説しています!
双対問題を作る
それでは公式に従って双対問題を作ってみましょう。
主問題:
\(\min \;\;\; c^\top x\)
\(\;\text{s.t.}\;\;\;Ax \leq b \)
\(\;\;\;\;\;\;\;\;\; x \geq 0\)
双対問題:
\(\max \;\;\; b^\top y\)
\(\;\text{s.t.}\;\;\;A^\top y \geq c \)
\(\;\;\;\;\;\;\;\;\; y\geq 0\)
\(c=\begin{pmatrix}1\\1\\1\\1\\1\\1\end{pmatrix}, x=\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\\x_{4}\\x_{5}\\x_{6}\end{pmatrix}\)
\(A = \begin{pmatrix}1&1&0&0&0&0\\1&0&1&0&0&0\\0&1&1&0&0&0\\0&1&0&1&0&0\\0&0&1&0&1&0\\0&0&0&1&1&0\\0&0&0&0&1&1\end{pmatrix} , b= \begin{pmatrix}1\\1\\1\\1\\1\\1\\1\end{pmatrix}\)
双対問題で使う変数\(y\)を以下のように定義します。
\(y = \begin{pmatrix}y_{12}\\y_{13}\\y_{23}\\y_{24}\\y_{35}\\y_{45}\\y_{56}\end{pmatrix}\)
まず目的関数は\(b^\top y\)なので以下のようになります。
\(b^\top y = \begin{pmatrix}1&1&1&1&1&1&1\end{pmatrix}\begin{pmatrix}y_{12}\\y_{13}\\y_{23}\\y_{24}\\y_{35}\\y_{45}\\y_{56}\end{pmatrix}\)
\(\;\;\;\;\;\;\;\;\;\;\;\;\;=y_{12}+y_{13}+y_{23}+y_{24}+y_{35}+y_{45}+y_{56}\)
制約条件は以下のように表せます。
\(\begin{pmatrix}1&1&0&0&0&0&0\\1&0&1&1&0&0&0\\0&1&1&0&1&0&0\\0&0&0&1&0&1&0\\0&0&0&0&1&1&1\\0&0&0&0&0&0&1\end{pmatrix} \begin{pmatrix}y_{12}\\y_{13}\\y_{23}\\y_{24}\\y_{35}\\y_{45}\\y_{56}\end{pmatrix}=\begin{pmatrix}y_{12}+y_{13}\\y_{12}+y_{23}+y_{24}\\y_{13}+y_{23}+y_{35}\\y_{24}+y_{45}\\y_{35}+y_{45}+y_{56}\\y_{56}\end{pmatrix} \leq \begin{pmatrix}1\\1\\1\\1\\1\\1\end{pmatrix}\)
これに変数\(y\)の非負制約も加えてまとめると、この最小頂点被覆問題の双対問題は以下のようになります。
目的関数(最大化):
\(y_{12} + y_{13} + y_{23} + y_{24}+ y_{35} + y_{45} + y_{56}\)
制約条件:
\(y_{12}+y_{13} \leq 1\)
\(y_{12}+y_{23}+y_{24} \leq 1\)
\(y_{13}+y_{23}+y_{35} \leq 1\)
\(y_{24}+y_{45} \leq 1\)
\(y_{35}+y_{45}+y_{56} \leq 1\)
\(y_{56} \leq 1\)
\(y_{12},y_{13},y_{23},y_{24},y_{35},y_{45},y_{56} \geq 0\)
双対問題から分かること
双対問題をより一般的に表す
双対問題:
\(\max \;\;\; \sum\limits_{e \in E}y_e\)
\(\;\;\; \text{s.t} \;\;\; \sum\limits_{e \in \delta(i)}y_e \leq 1 \;\;\; (\forall i \in V)\)
\(\;\;\;\;\;\;\;\;\; y_e \geq 0 \;\;\; (\forall e \in E)\)
\(V\):頂点集合
\(E\):辺集合
\(\delta(i)\):頂点\(i\)に接続する辺集合
ここまでは具体例を使って最小頂点被覆問題(を線形緩和した問題)の双対問題を求めましたが、より一般的に双対問題を表すと上記のようになります。
制約条件の係数行列\(A\)がグラフの接続行列の転置行列であることを考えたら理解しやすいと思います。
双対問題が最大マッチング問題になっている
この双対問題をよく見ると、最大マッチング問題を線形緩和した問題と一致していることが分かります。
最大マッチング問題はこちらの記事で詳しく解説しています!
最大マッチング問題:
\(\max \;\;\; \sum\limits_{e \in E}x_e\)
\(\;\;\; \text{s.t} \;\;\; \sum\limits_{e \in \delta(i)}x_e \leq 1 \;\;\; (\forall i \in V)\)
\(\;\;\;\;\;\;\;\;\; x_e \geq 0 \;\;\; (\forall e \in E)\)
\(V\):頂点集合
\(E\):辺集合
\(\delta(i)\):頂点\(i\)に接続する辺集合
最大マッチング問題は上記のような整数計画問題として定式化できますが、変数\(x_e\)を線形緩和することでさっきの双対問題と同じ問題になります。
上の整数計画問題を線形緩和したら\(0 \leq x_e \leq 1\)となりますが、\(x_e \leq 1\)は必要のない制約です。というのも\(\sum\limits_{e \in \delta(i)}x_e \leq 1\)が成り立てば\(x_e \leq 1\)は成り立つからです。
最大マッチングと最小頂点被覆の関係
\(\textbf{(最大マッチングの要素数)}\leq \textbf{(最小頂点被覆の要素数)}\)
実はこれまでの話から上記のことが成り立ちます。

例えば上図の左側のグラフの場合、最大マッチングの要素数と最小頂点被覆の要素数がともに3なので
\(\textbf{(最大マッチングの要素数)}= \textbf{(最小頂点被覆の要素数)}\)
となっています。一方右側のグラフの場合、最大マッチングの要素数が3、最小頂点被覆の要素数が4なので
\(\textbf{(最大マッチングの要素数)}< \textbf{(最小頂点被覆の要素数)}\)
となっています。これ実は全てのグラフで成立するんです。これは先ほどまで考えてた最小頂点被覆問題と最大マッチング問題の双対性から分かります。
これは各頂点のコストが1の最小頂点被覆問題のときの話です。
詳しい話はこちらの記事で解説しています!
現在制作中
おわりに
いかがでしたか。
今回の記事では最小頂点被覆問題について解説していきました。
今後もこのような数理最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。