～離散型確率分布と連続型確率分布ってなに？～統計検定2級を勉強してみよう！【経営工学を専門にしている大学生の日記】

はじめに

こんにちは！しゅんです！

今回は離散型確率分布と連続型確率分布について解説していきます！

これらは確率・統計で登場する数学用語です。この記事では離散型確率分布と連続型確率分布について図を使って分かりやすく解説していきます。

それでは解説していきましょう！

統計検定2級に関する他の記事はこちらから見れます！
ぜひ他の記事も読んでみてください！

もっとみる

このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。

このブログについて

このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます！

ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。

そもそも経営工学とは何なのでしょうか。Wikipediaによると

経営工学（けいえいこうがく、英: engineering management）は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。

引用元 : 経営工学 – Wikipedia

長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。

確率分布ってなに？

確率分布を簡単に説明すると、どのような現象がどのような確率で発生するかをまとめたものです。例えばサイコロの例を考えてみましょう。

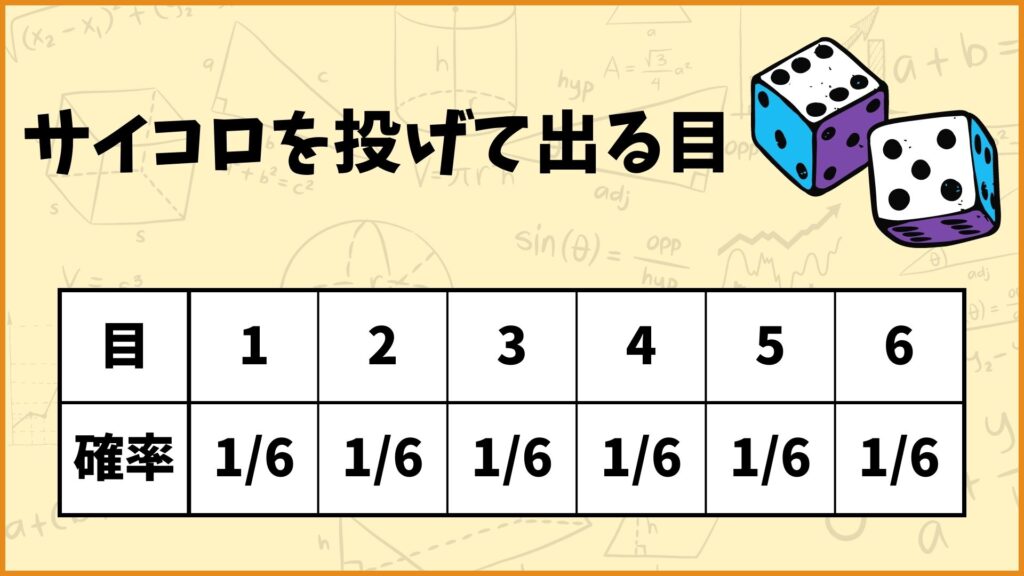
この図にある表はサイコロを投げたときにどの目がどれくらいの確率で出るかをまとめています。当然どの目も出る確率は一緒なので、確率は全て\(\frac{1}{6}\)になります。

このようにとある結果になる確率がいくつになるかというのをまとめたものを確率分布と言います。確率分布はよく関数やグラフを使って表されます。例えばサイコロの例で言うと関数とグラフは下のようになります。

確率関数

\(f(x) = \frac{1}{6}\)　　　\((x=1,2,3,4,5,6)\)

どちらも出る目が1,2,3,4,5,6のいずれにおいても確率が\(\frac{1}{6}\)だよってことを表しています。

確率分布は2種類ある

確率分布には大きく分けて離散型確率分布と連続型確率分布の2種類があります。これらの違いは考えている現象が取りうる値がとびとびかそうじゃないかです。

離散型確率分布：取りうる値がとびとび
連続型確率分布：取りうるあたいがとびとびじゃない

言葉だけじゃ少し難しいので具体例を使って説明したいと思います。

サイコロは離散型確率分布

確率分布の説明で話したように確率分布とはとある現象がどのような確率で起こるかをまとめたものです。サイコロの例でいう現象は出た目の数です。

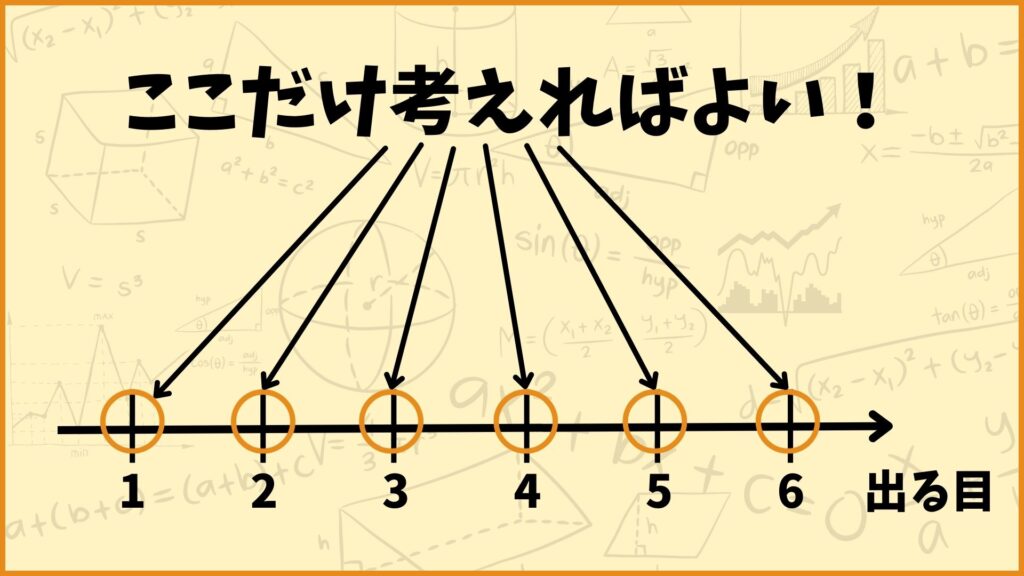
つまりサイコロを振った時にどの目が出るかを考えるときは1,2,3,4,5,6の6パターンについてだけ考えれば良いです。このことを考えている現象が取りうる値がとびとびであると表現しています。

例えばサイコロを投げたときに出た目が4.5だったなんてことは起こりません。

他にも例えばコイントスは離散型確率分布です。コイントスで起こりうる現象はおもて(1)が出るかうら(0)が出るかの2パターンしかありません。

身長は連続型確率分布

連続型確率分布は考えている現象の取りうる値がとびとびじゃないものです。例えば身長について考えてみましょう。

サイコロの場合は例えば4.5を取る可能性は0だったわけですが、身長の場合は例えば170.2cmを取る可能性もあります。サイコロと違って身長は全ての実数を考える必要があります。

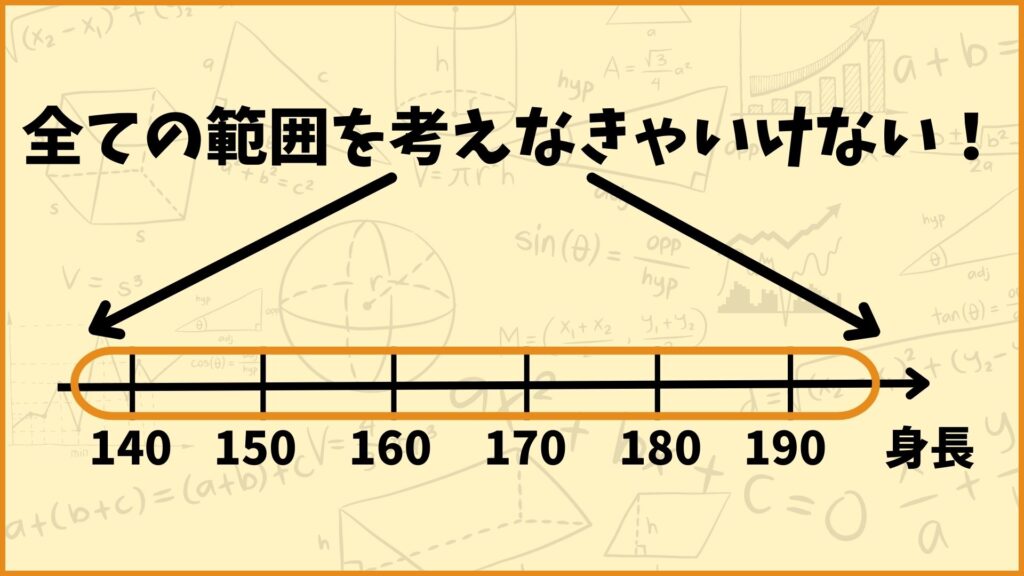
このことを考えている現象が取りうる値がとびとびじゃないと表現しています。

他にも例えば体重は連続型確率分布です。体重もすべての実数を取りうるので無限のパターンが考えられます。

ということでここまで離散型確率分布と連続型確率分布の違いを図を使って解説しましたが、次の章からはより数学的な違いについて説明したいと思います。

離散型確率分布と連続型確率分布のグラフの見方

離散型確率分布と連続型確率分布の大きな違いの一つに、グラフの見方があります。この章ではそれぞれどういう風にグラフを解釈すれば良いのかについて解説したいと思います。

離散型確率分布

離散型確率分布の例としてコイントスを5回行ったときに何回おもてが出たかを考えましょう。

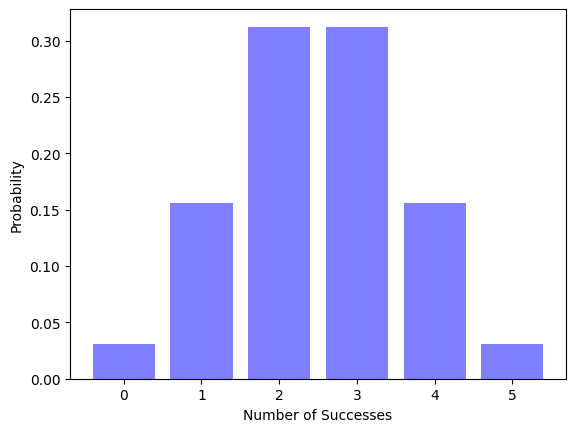
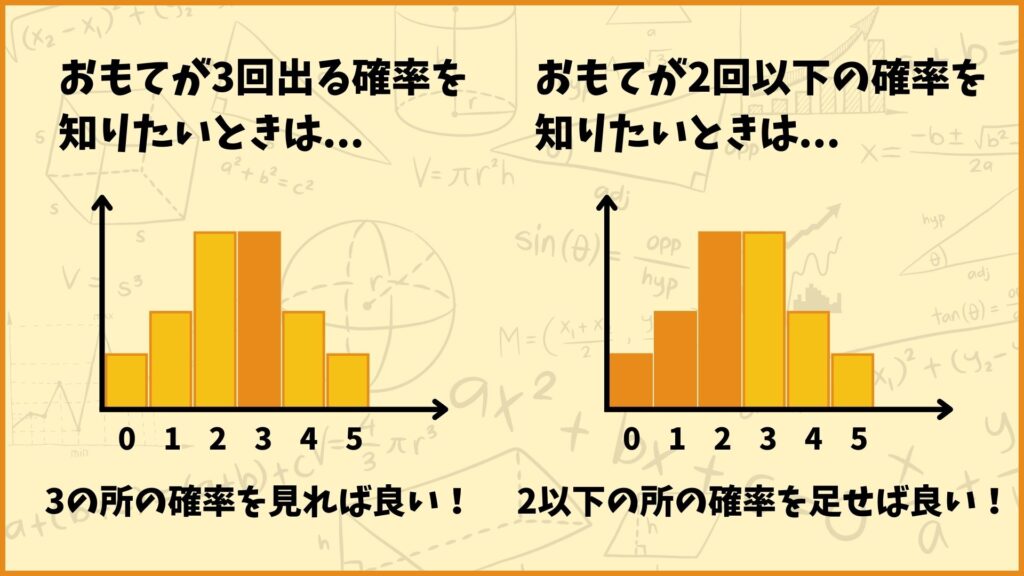
このグラフは横軸をおもてが出た回数、縦軸をその回数になる確率を取っています。このグラフから、例えばおもてが3回出る確率を調べたいときは横軸が3の所の確率を見れば良い訳です。（このグラフだと0.3をちょっと超えているくらいですね。）

他にも例えばおもてが出る回数が2回以下になるような確率を調べたいときは、横軸が0,1,2の所の確率を全て足せば求めることができます。

連続型確率分布

連続型確率分布の例として標準正規分布のグラフを見てみましょう。

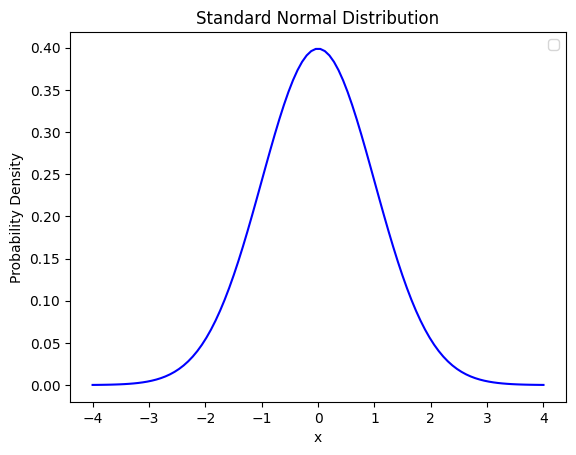
離散型確率分布のときとは違ってグラフが棒グラフではありませんね。連続型確率分布をグラフで表すときに棒グラフは使いません。

なぜかというと連続型確率分布は全ての実数に対して確率が与えられるはずなので、一個一個棒グラフを書いていこうと思ったら棒グラフが無限に必要になってしまいます。

またこのグラフの読み取り方も離散型確率分布とは異なります。例えばこのグラフにおいて\(x=0\)となる確率はいくつになるでしょうか。

ぱっと見0.40くらいかな～って思うかもしれませんが、結論\(x=0\)となる確率は0です。ここすごい重要で、連続型確率分布の場合は\(x=…\)のようにとある1点における確率は0になってしまいます。

例えば身長が170cmである確率を考えてみましょう。周りの友達を見ると身長が170cmの人はけっこういると思います。しかしその人たちは本当は身長が170.1cmかもしれないし、169.998cmかもしれないし、170.000000001cmかもしれないですよね。このような場合厳密には身長170cmではありません。そう考えたら身長が170cmである確率って0じゃないですかね。

これが連続型確率分布と離散型確率分布の大きな違いの1つです。では連続型確率分布はどのように扱えばよいのでしょうか。

ポイントは面積です。離散型確率分布の大きな特徴は確率を面積で考えるということです。下の図を見てください。

さきほどの連続型確率分布においてxが-1から1の間になる確率を求めることを考えます。このグラフと横軸で囲まれた範囲の面積が実は求めたい確率になるんです。この図で言ったらオレンジの斜線部の面積がxが-1から1の間になる確率です。

連続型確率分布のグラフは言ってしまえば確率がどれくらい詰まっているかを表しています。そのためこのグラフのことを確率密度関数って言います。

離散型確率分布

確率（質量）関数