- 焼きなまし法ってなに?
- 割当問題ってなに?
- 焼きなまし法で割当問題の解を求めたい…
こんにちは!しゅんです!
今回は焼きなまし法で割当問題を解く方法について解説していきます!
割当問題は組合せ最適化の代表的な問題で、焼きなまし法は最適化問題を解く方法の1つです。
それではやっていきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
焼きなまし法ってなに?
最適化問題の中でも最小化問題を例に、焼きなまし法の説明を行いたいと思います。
簡単な説明
焼きなまし法を簡単に説明すると
焼きなまし法:
初期解から解を少しずつ変えていって目的関数がより小さくなる解に移動する。このとき、とある確率で目的関数が大きくなる解にも移動する。
です。最初の「目的関数がより小さくなる解に移動する」というのは納得できますが、後半の
とある確率で目的関数が大きくなる解にも移動する
という部分がよく分からないですね。

上図を見てみましょう。上のグラフは目的関数を表していると考えてください。いま橙〇にいると仮定します。ここで赤〇に移動するかどうかを考えます。目的関数値の大小関係を考えたら
橙:目的関数値 小
赤:目的関数値 大
となるので赤〇には移動しないはずです。ところが焼きなまし法ではある数式で計算される確率に従って、赤〇に移動することがあります。
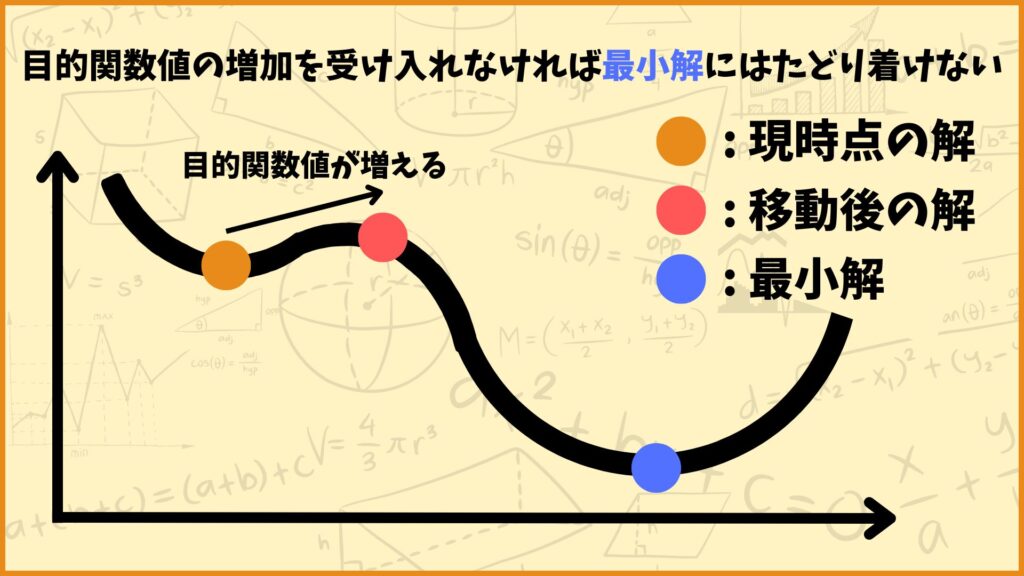
この目的関数の形を見ると、橙〇の周りの解は全て橙〇よりも目的関数値が大きくなるので、目的関数値の増加を受け入れなければ橙〇から動くことができず、最小解の青〇まで行くことができません。
しかし目的関数値の増加を受け入れ、赤〇に移動する可能性があればそこから最小解の青〇に移動することもできます。
このように焼きなまし法では局所最適解にとどまってしまうのを防ぐために、とある確率で目的関数が大きくなる解にも移動するようなアルゴリズムになっているんです。
数式を使った説明
焼きなまし法ではまず
初期解:\(S_0\)
初期温度:\(T_0\)
を用意します。初期温度については後で説明します。
初期解と初期温度を設定したら、以下の操作を反復して行います。なお、説明で近傍解という言葉を使っていますが、これは今の解にちょっとだけ変更を加えた解というイメージを持ってください。
STEP 1:
現在の解 \(S\) からその近傍解 \(S’\) を用意する。
STEP 2:
2つの解における目的関数値の差を計算する。すなわち
\(\Delta E = E(S’)-E(S)\)
を計算する。(但し \(E(S)\) は解 \(S\) における目的関数値を表す。)
STEP 3:
\(\Delta E < 0\) の場合、現在の解を \(S’\) に更新する。
\(\Delta E \geq 0\) の場合、確率 \(P = \exp(-\frac{\Delta E}{T})\) で現在の解を \(S’\) に更新する。
STEP 4:
温度を低くする。(例えば冷却率 \(\alpha\) を用いて温度を \(T \to \alpha T\) に更新する。)
この操作を繰り返し行い、温度が十分低くなるか、自分で決める最大反復回数に達したら解の更新を終了します。
STEP 1とSTEP 2については特に解説するところが無いので、STEP 3とSTEP 4について説明します。
STEP 3の説明
STEP 2で現在の解とその近傍解の目的関数値の差を計算しました。例えば
\(E(S) = 12\)
\(E(S’)= 10\)
だったとします。このとき
\(\Delta E = E(S’)-E(S)=10-12=-2<0\)
となり、解を \(S\) から \(S’\) に更新すると目的関数値が小さくなります。従って現在の解を\(S\) から \(S’\) に更新します。
目的関数値が最小となる解を見つけるのが目的なので、この操作に違和感はないと思います。
では次に
\(E(S) = 7\)
\(E(S’)= 9\)
だった場合を考えます。このとき
\(\Delta E=E(S’)-E(S)= 9-7=2>0\)
となります。直観的に考えると、現在の解 \(S\) よりも近傍解 \(S’\) の方が目的関数値が大きいので解の更新は行わないのが自然です。ですが焼きなまし法では下の式で計算される確率で解を更新します。
\(P = \exp(-\frac{\Delta E}{T})\)
例えば現在の温度が \(T=10\) の場合
\(P =\exp(-\frac{\Delta E}{T})=\exp(-\frac{2}{10})≒0.82\)
と計算できます。すなわち82%の確率で現在の解を \(S\) から \(S’\) に更新します。
STEP 4の説明
STEP 4では温度を低くします。この記事では
冷却率 \(\alpha\) を用いて、温度を \(T \to \alpha T\) に更新する
という方法で温度をどんどん低くしていきます。例えば初期温度 \(T_0 = 100\)、冷却率 \(\alpha = 0.95\) とすると各反復ごとに温度は
0回目:100
1回目:95
2回目:90.25
3回目:85.7375
4回目:81.4506…
5回目:77.3781…
という感じで低くなっていきます。STEP 3で説明した確率 \(P\) は温度 \(T\) が低くなるほど小さくなるので、
反復回数が大きくなるにつれ、目的関数が悪化する解に移動する確率は低くなる
ということを表しています。
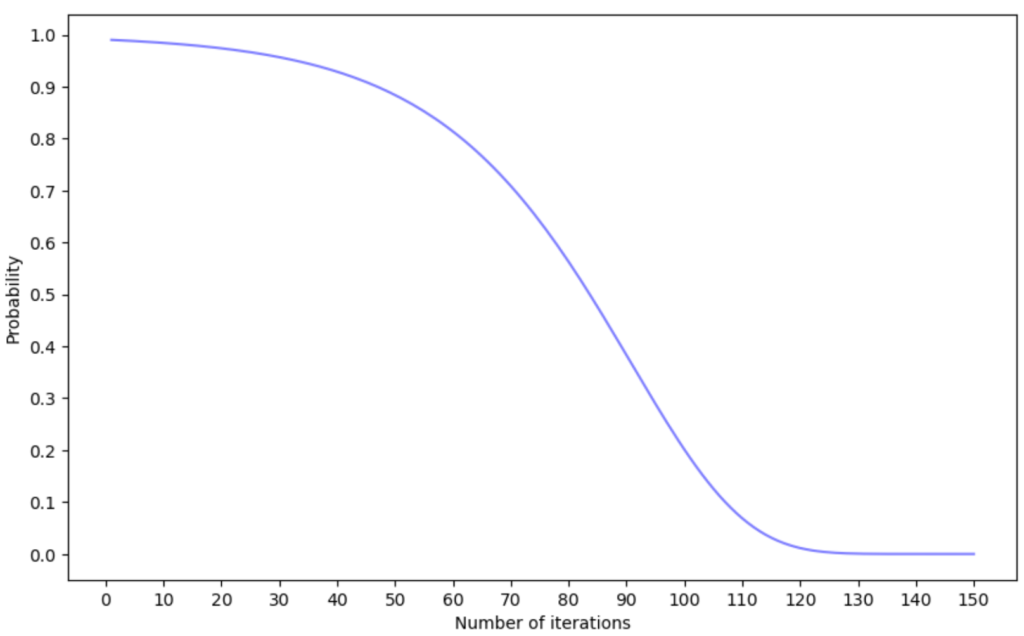
上図は \(\Delta E = 1, T_0 = 100, \alpha = 0.95\) のとき、横軸を反復回数、縦軸を確率にしたときのグラフを表しています。
これを見ると、最初のうちは確率が高いですが、段々確率が小さくなり、120回を超えたあたりから確率がほぼ0になっていることが分かります。
焼きなまし法はヒューリスティック解法の1つ
焼きなまし法はヒューリスティック解法の1つです。ヒューリスティック解法を簡単に説明すると
ヒューリスティック解法:
最適解を求めるのが難しい問題に対して、ある程度のレベルで最適解に近い解を効率的に求める解法
です。焼きなまし法では最大反復回数を設定したり、温度の閾値を設定したりして計算を途中で終了してその時点での解を出力しまが、その解が最適解であるとは限りません。
ヒューリスティック解法は解くのが難しい問題(NP困難)に対して使われる手法なのですが、この記事で扱う割当問題は、既に多項式時間で最適解を得られるアルゴリズム(ハンガリー法)が考案されています。
そのため本当はヒューリスティック解法を使う必要がないのですが、今回は勉強のために割当問題を例に焼きなまし法を実装したいと思います。
割当問題ってなに?
過去の記事で割当問題について詳しく説明しているので、ここでは簡単に説明したいと思います。
具体例を使って説明する
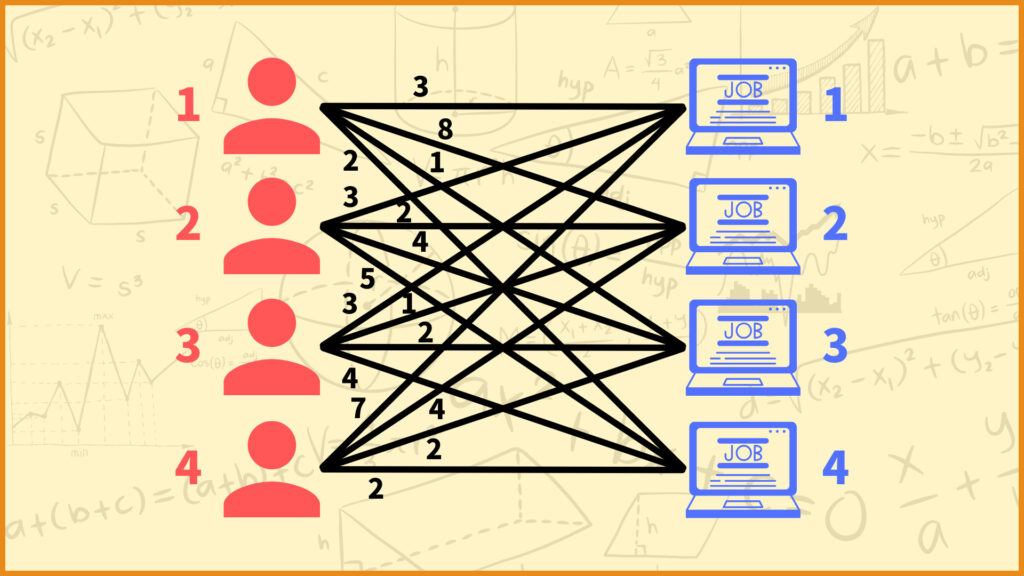
例えば4人の従業員と4個の仕事があり、各従業員に1つの仕事を割り当てるときに、どのように割り当てたら最も効率的になるかを考える問題が割当問題です。よくある問題例だと制約条件として
制約条件:
・各従業員は1つの仕事を担当する。
・各仕事は1人の従業員に割り当てられる。
というものです。また目的関数としてよくあるのは
目的関数(最小化):
従業員を仕事に割り当てるときにかかるコストの合計
というものです。すなわちコストの合計が最小となるような割り当て方を求める割当問題です。
整数計画問題として定式化する
整数計画問題として定式化すると下のようになります。
パラメータ
\(V\):従業員の集合
\(W\):仕事の集合
\(c_{ij}\):従業員 \(i\) を仕事 \(j\) に割り当てるときのコスト
変数
\(x_{ij}\in\{0,1\}\):従業員 \(i\) を仕事 \(j\) に割り当てるなら1、そうでないなら0を取る0-1変数
整数計画問題として定式化:
\(\min \;\;\; \sum\limits_{i \in V} \sum\limits_{j \in W} c_{ij}x_{ij}\)
\(\;\text{s.t.}\;\;\;\sum\limits_{j \in W} x_{ij}=1 \;\;\;\; (\forall i \in V)\)
\(\;\;\;\;\;\;\;\;\;\sum\limits_{i \in V} x_{ij}=1 \;\;\;\; (\forall j \in W)\)
\(\;\;\;\;\;\;\;\;\; x_{ij} \in \{0,1\} \;\;(\forall i \in V \; \forall j \in W)\)
従業員と仕事の例を挙げて説明しましたが、それ以外にも例えば「警察官とパトロール地域」や「トラックのドライバーと配送ルート」など色々な例があります。
pythonを使って焼きなまし法で割当問題を解いてみた
それでは実際にpythonを使って焼きなまし法で割当問題を解いてみましょう。コードが少し長いので、結果だけ見たい方は「コードの解説」の部分は飛ばしてください。
また近傍解に作り方に関しては
近傍解の作り方:
現在の解からランダムに2つの要素を選んで入れ替える
とします。例えば現在の解が
従業員1 ー 仕事3
従業員2 ー 仕事1
従業員3 ー 仕事4
従業員4 ー 仕事2
のとき、ランダムに2つの仕事を選んで入れ替えます。例えば仕事3と仕事4を入れ替えて得られる近傍解は
従業員1 ー 仕事4
従業員2 ー 仕事1
従業員3 ー 仕事3
従業員4 ー 仕事2
となります。
コードの解説
## 必要なライブラリをインポート
import numpy as np
import random
import copy
import math
np.random.seed(42)
## コストの合計を計算する関数を定義
def calculate_total_cost(cost_matrix, assignment):
total_cost = 0
for i, j in enumerate(assignment):
total_cost += cost_matrix[i][j]
return total_cost
## 近傍解を生成する関数を定義
def generate_neighbor(assignment):
neighbor = copy.deepcopy(assignment)
i, j = random.sample(assignment, 2)
neighbor[i], neighbor[j] = neighbor[j], neighbor[i]
return neighbor
## 焼きなまし法を実装する関数を定義
def simulated_annealing(cost_matrix, initial_temp, cooling_rate, max_iter):
# 初期解の生成(ランダムな割り当て)
current_assignment = list(range(len(cost_matrix)))
random.shuffle(current_assignment)
current_cost = calculate_total_cost(cost_matrix, current_assignment)
# 最良解の初期化
best_assignment = copy.deepcopy(current_assignment)
best_cost = current_cost
# 温度の初期化
temperature = initial_temp
# 最大反復回数(max_iter)まで繰り返し操作を行う
print("------------------------計算開始")
for iteration in range(max_iter):
neighbor = generate_neighbor(current_assignment) # generate_neighbor関数を使って近傍解の生成
neighbor_cost = calculate_total_cost(cost_matrix, neighbor) # calculate_total_cost関数を使って近傍解の目的関数値を計算
# 目的関数値の差の計算
delta_E = neighbor_cost - current_cost
# 解の受け入れ判定
if delta_E < 0:
# 目的関数値が改善された場合は受け入れる
current_assignment = neighbor
current_cost = neighbor_cost
# その時点での最良解より目的関数値が小さかったら再良解を更新
if neighbor_cost < best_cost:
best_assignment = neighbor
best_cost = neighbor_cost
else:
# 目的関数値が悪化した場合は確率的に受け入れる
acceptance_prob = math.exp(-delta_E / temperature) # 受け入れる確率を計算
if random.random() < acceptance_prob: # 0以上1以下のランダムに生成した実数が確率値より小さかったら解を受け入れる
current_assignment = neighbor
current_cost = neighbor_cost
# 温度の更新
temperature *= cooling_rate
# 終了条件(温度が十分低くなった場合)
if temperature < 1e-20:
break
# デバッグ用: 進捗表示
if iteration % 1000 == 0:
print(f"反復回数 {iteration}: 目的関数値 = {best_cost}")
print("------------------------計算終了")
return best_assignment, best_cost
## 問題例を入力して結果を出力する
# コスト行列を設定
n = 10 # 割当問題のサイズ
cost_matrix = np.random.randint(1, 11, size=(n, n)) # コスト行列を計算
# パラメータの設定
initial_temperature = 1000
cooling_rate = 0.995
max_iterations = 10001
# 焼きなまし法の実行
best_assignment, best_cost = simulated_annealing(cost_matrix, initial_temperature, cooling_rate, max_iterations)
# 結果の表示
print("最良の割り当て:", best_assignment)
print("目的関数値:", best_cost)
長いので分けて説明します。
必要なライブラリをインポート
## 必要なライブラリをインポート
import numpy as np
import random
import copy
import math
np.random.seed(42)
ここでは必要なライブラリとして「numpy」、「random」、「copy」をインポートしています。
「numpy」は数値計算を効率的に行うために使います。
「random」はランダムな数字を生成するために使います。
「copy」は2次元リストをコピーするために使います。
「math」は指数の計算をする際に使います。
コストの合計を計算する関数を定義
## コストの合計を計算する関数を定義
def calculate_total_cost(cost_matrix, assignment):
total_cost = 0
for i, j in enumerate(assignment):
total_cost += cost_matrix[i][j]
return total_cost
ここでは入力された解のコストの合計(目的関数値)を求める関数を定義しています。
2行目では「calculate_total_cost」関数を定義しています。引数はそれぞれ「cost_matrix」がコスト行列、「assignment」が解を表しています。
「cost_matrix」は2次元行列で「cost_matrix[i][j]」が \(c_{ij}\) を表しています。
「assignment」は1次元リストで、例えば従業員0が仕事1、従業員1が仕事3、従業員2が仕事2、従業員4が仕事0を担当する場合「assignment = [1,3,2,0]」となります。
3行目ではコストの合計の初期値を設定しています。
4~5行目ではコストの合計を求めています。
6行目ではコストの合計を返しています。
近傍解を生成する関数を定義
## 近傍解を生成する関数を定義
def generate_neighbor(assignment):
neighbor = copy.deepcopy(assignment)
i, j = random.sample(assignment, 2)
neighbor[i], neighbor[j] = neighbor[j], neighbor[i]
return neighbor
ここでは入力された解の近傍解を生成する関数を定義しています。
2行目では「generate_neighbor」関数を定義しています。引数の「assignment」は解を表しています。
3行目では入力された解のコピーを取得しています。
4行目では「assignment」からランダムに2つ異なる要素を取得しています。
5行目では4行目で取得した2つの要素を入れ替えて近傍解を作成しています。
6行目では近傍解を返しています。
焼きなまし法を実装する関数を定義
## 焼きなまし法を実装する関数を定義
def simulated_annealing(cost_matrix, initial_temp, cooling_rate, max_iter):
# 初期解の生成(ランダムな割り当て)
current_assignment = list(range(len(cost_matrix)))
random.shuffle(current_assignment)
current_cost = calculate_total_cost(cost_matrix, current_assignment)
# 最良解の初期化
best_assignment = copy.deepcopy(current_assignment)
best_cost = current_cost
# 温度の初期化
temperature = initial_temp
# 最大反復回数(max_iter)まで繰り返し操作を行う
print("------------------------計算開始")
for iteration in range(max_iter):
neighbor = generate_neighbor(current_assignment) # generate_neighbor関数を使って近傍解の生成
neighbor_cost = calculate_total_cost(cost_matrix, neighbor) # calculate_total_cost関数を使って近傍解の目的関数値を計算
# 目的関数値の差の計算
delta_E = neighbor_cost - current_cost
# 解の受け入れ判定
if delta_E < 0:
# 目的関数値が改善された場合は受け入れる
current_assignment = neighbor
current_cost = neighbor_cost
# その時点での最良解より目的関数値が小さかったら再良解を更新
if neighbor_cost < best_cost:
best_assignment = neighbor
best_cost = neighbor_cost
else:
# 目的関数値が悪化した場合は確率的に受け入れる
acceptance_prob = math.exp(-delta_E / temperature) # 受け入れる確率を計算
if random.random() < acceptance_prob: # 0以上1以下のランダムに生成した実数が確率値より小さかったら解を受け入れる
current_assignment = neighbor
current_cost = neighbor_cost
# 温度の更新
temperature *= cooling_rate
# 終了条件(温度が十分低くなった場合)
if temperature < 1e-20:
break
# デバッグ用: 進捗表示
if iteration % 1000 == 0:
print(f"反復回数 {iteration}: 目的関数値 = {best_cost}")
print("------------------------計算終了")
return best_assignment, best_cost
ここでは焼きなまし法を実装しています。
2行目では「simulated_annealing」関数を定義しています。引数はそれぞれ「cost_matrix」がコスト行列、「initial_temp」が初期温度、「cooling_rate」が冷却率、「max_iter」が最大反復回数を表しています。
4~5行目では初期解を生成しています。初期解はランダムに設定しています。
6行目では初期解のコストの合計(目的関数値)を計算しています。
8~9行目で最良解の初期化をしています。8行目で初期解を最良解を、9行目で初期コストを最良コストに設定しています。
11行目で初期温度を設定しています。
14行目からは焼きなまし法の反復操作を実装しています。
15行目では「generate_neighbor」関数を使って現在の解の近傍解を生成しています。
16行目では「calculate_total_cost」関数を使って近傍解のコストの合計(目的関数値)を計算しています。
18行目では現在の解と近傍解の目的関数値の差を計算しています。
20~22行目では、\(\Delta E<0\) の場合に現在の解を近傍解に設定しています。それに伴い23行目では現在の解の目的関数値を近傍解の目的関数値に設定しています。
25~27行目では、近傍解の目的関数値がこれまでの最良解の目的関数値より小さかったら最良解を近傍解に更新しています。
28行目からは \(\Delta E \geq 0\)の場合の操作を実装しています。
30行目で解を受け入れる確率を求めています。
31行目では、「random.random()」によってランダムに生成された0以上1以下の実数が30行目で計算した確率の値より小さいかどうかを判定しています。
32行目では現在の解を近傍解に更新しています。
33行目では目的関数値を近傍解の目的関数値に更新しています。
35行目では現在の温度に冷却率 \(\alpha\) を掛けています。
37~38行目では温度が \(10^{-20}\)より小さくなったら反復を終了します。
40~41行目では、反復回数1000回ごとに進捗を表示しています。
43行目で焼きなまし法の実行結果として、最良解と最良解の目的関数値を出力しています。
問題例を入力して結果を出力する
## 問題例を入力して結果を出力する
# コスト行列を設定
n = 10 # 割当問題のサイズ
cost_matrix = np.random.randint(1, 11, size=(n, n)) # コスト行列を計算
# パラメータの設定
initial_temperature = 1000
cooling_rate = 0.995
max_iterations = 10001
# 焼きなまし法の実行
best_assignment, best_cost = simulated_annealing(cost_matrix, initial_temperature, cooling_rate, max_iterations)
# 結果の表示
print("最良の割り当て:", best_assignment)
print("目的関数値:", best_cost)
ここでは問題例を入力して焼きなまし法を実行して結果を出力しています。
3行目で問題のサイズを設定しています。今回は10人の従業員を10個の仕事に割り当てる問題を解きます。
4行目ではコスト行列をランダムに生成しています。コストは1以上10以下の整数です。
6行目では初期温度、7行目では冷却率、8行目では最大反復回数をそれぞれ設定しています。
10行目では焼きなまし法を実行して結果を取得しています。
12行目で最良解を表示しています。
13行目で最良解の目的関数値を表示しています。
結果を確認する

このコードを実行したら上の結果が得られました。これを見ると反復回数が2000の時点で目的関数値が20になっていて、それ以降の反復では目的関数値が変わっていないですね。
最良の割り当てを見ると
従業員0 ー 仕事6
従業員1 ー 仕事9
従業員2 ー 仕事5
従業員3 ー 仕事8
従業員4 ー 仕事1
従業員5 ー 仕事3
従業員6 ー 仕事4
従業員7 ー 仕事2
従業員8 ー 仕事7
従業員9 ー 仕事0
という解が出力されています。
目的関数値は20が出力されています。はたしてこの値は最適値なのでしょうか。
最適値とのギャップを調べる
ということで焼きなまし法で得られた目的関数値が本当に最適値なのかを確かめてみましょう。第3章の割当問題の説明の所で整数計画問題として定式化しましたが、それを使って最適値を求め、ギャップを求めたいと思います。
実は第3章で定式化した割当問題は0-1変数を線形緩和して、0以上の連続変数として解いても整数最適解が得られるという性質があるんです。線形計画問題を解く方が計算時間が短いので、この後登場するプログラムは線形緩和した問題を解いて最適値を求めます。
## 事前準備
import pulp # pulpをインポート
from pulp import LpMinimize, LpVariable, lpSum, LpStatus
def LP_solve(V,W,cost_matrix):
## 整数計画問題の設定
prob = pulp.LpProblem(sense = LpMinimize) # 問題をMinimizeに設定
x = LpVariable.dict("x",(V,W), cat = "Continuous") # 0-1変数の設定
prob += lpSum(x[i,j] * cost_matrix[i][j] for i in V for j in W) # 目的関数の設定
for i in V:
prob += lpSum(x[i,j] for j in W) == 1 # 従業員側の頂点に関する制約条件を設定
for j in W:
prob += lpSum(x[i,j] for i in V) == 1 # 仕事側の頂点に関する制約条件を設定
for i in V:
for j in W:
prob+= x[i,j] >= 0
result = prob.solve() # 問題を解く
return prob.objective.value()np.random.seed(42)
## 問題例を入力して結果を出力する
# パラメータの設定
initial_temperature = 1000
cooling_rate = 0.995
max_iterations = 10001
n_list = [n for n in range(5,201,5)]
best_value_list = []
opt_value_list = []
# コスト行列を設定
for n in n_list:
V = [i for i in range(n)]
W = [j for j in range(n)]
cost_matrix = np.random.randint(1, 11, size=(n, n)) # コスト行列を計算
# 焼きなまし法の実行
best_assignment, best_value = simulated_annealing(cost_matrix, initial_temperature, cooling_rate, max_iterations)
opt_value = LP_solve(V,W,cost_matrix)
best_value_list.append(best_value)
opt_value_list.append(opt_value)
print(f"n = {n}の計算が終わりました。")import matplotlib.pyplot as plt
import numpy as np
best_value_list = np.array(best_value_list)
opt_value_list = np.array(opt_value_list)
gap_list = 100*((best_value_list/opt_value_list)-1)
# 図と主な軸の作成
fig, ax1 = plt.subplots(figsize=(10, 6))
# 主なy軸(左側)にbest_value_listとopt_value_listをプロット
line1, = ax1.plot(n_list, best_value_list, color="deepskyblue", label="Best Value", marker = ".")
line2, = ax1.plot(n_list, opt_value_list, color="limegreen", label="Optimal Value", marker = ".")
ax1.set_xlabel("n")
ax1.set_ylabel("Objective Value", color="black")
ax1.tick_params(axis='y', labelcolor="black")
ax1.set_ylim(-5, 270)
# 補助y軸(右側)を作成
ax2 = ax1.twinx()
# 補助y軸にgap_listをプロット
line3, = ax2.plot(n_list, gap_list, color="deeppink", label="Gap (%)", alpha = 0.5, marker = ".")
ax2.set_ylabel("Gap (%)")
ax2.set_ylim(-1,54)
ax2.tick_params(axis='y')
# 凡例の作成
# 各軸からラインを取得し、結合して凡例を作成
lines = [line1, line2, line3]
labels = [line.get_label() for line in lines]
ax1.legend(lines, labels, loc='upper left')
# グリッドの追加(任意)
ax1.grid(True, which='both', linestyle='--', linewidth=0.5)
# タイトルの追加(任意)
plt.title("Objective Value and Gap vs n")
# 図の表示
plt.show()
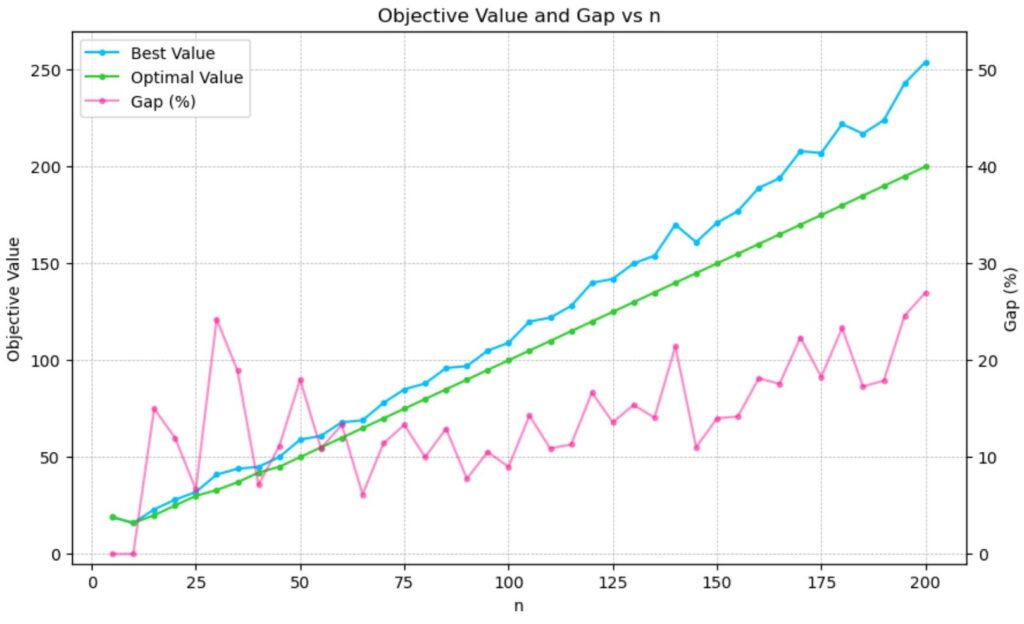
このグラフは横軸が問題のサイズ \(n\)、左側の縦軸が目的関数値、右側の縦軸がギャップをそれぞれ表しています。各グラフの意味はそれぞれ
青のグラフ:焼きなまし法で得られた解の目的関数値
緑のグラフ:最適値
赤のグラフ:緑のグラフと青のグラフのギャップ
を表しています。ギャップについて数式を使ってもう少し詳しく説明すると、
\(E_{best}\):焼きなまし法で得られた解の目的関数値
\(E_{opt}\):最適値
ギャップの計算式:\(100\times\frac{E_{best}-E_{opt}}{E_{opt}}\)
上の式で計算されます。これらのグラフを見ると結構ギャップがあることが分かりますね。もっと工夫をすればギャップの改善ができるかもしれません。
おわりに
いかがでしたか。
今回の記事では焼きなまし法と割当問題について解説しました。
今後もこのような組合せ最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。






