こんにちは!しゅんです!
今回は回帰と判別について解説していきたいと思います。
回帰と判別はデータ分析でまず勉強する大事な分析です。ぼくがデータ分析の勉強をしていたときに最初にでてきたので皆さんにもシェアしたいと思います!また今回は説明と一緒にpythonを使ってどんなものか確かめたいと思います。
それでは解説していきましょう!
普段はNBAのデータ分析をしたりしています。
ぜひこちらの記事も読んでみてください!
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
回帰ってなに?
回帰をザックリ説明すると与えられた情報から知りたい情報を求めることです。以下の例を見てみましょう。
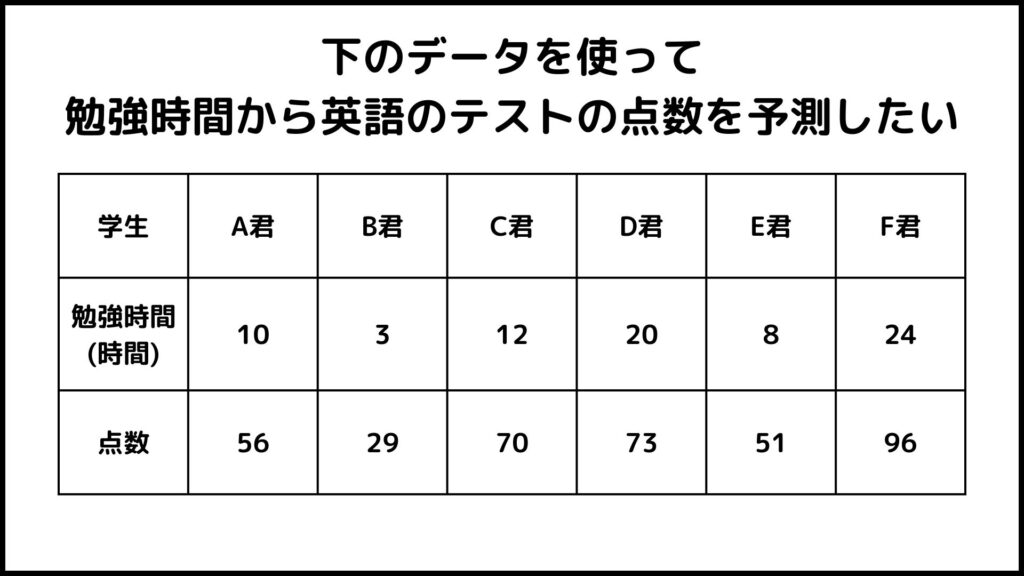
これはとある学校の学生の勉強時間とテストの点数データを集めたものです。このデータを使って勉強時間からテストの点数を予測することを考えます。
二つのデータの関係を見るのには散布図が便利です。
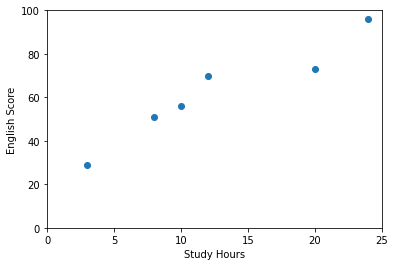
横軸が勉強時間で縦軸がテストの点数です。これを見ると勉強時間とテストの点数の間には正の相関関係がありそうですね。
回帰はこの関係を式で表して予測することです。例えば今回の例で言うとだいたい下のような直線が引けそうですね。
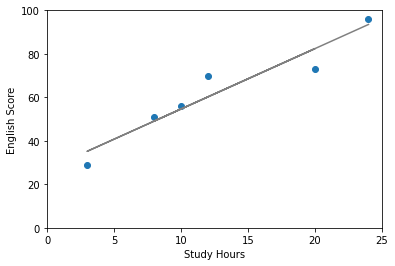
このグレーの直線は
点数 = 2.8 × 勉強時間 + 26.9
で表されます。もしこの式が分かれば、勉強時間からテストの点数が予測できます。
例えば勉強時間が15時間の生徒がテストで何点取れるのかを予測したい場合は
点数 = 2.8 × 15 + 26.9 = 68.9
となります。つまりだいたい69点くらい取れるということが予測できました。
以上のように回帰分析をすることで与えられている情報から知りたい情報を予測することが出来ます。
※与えられている情報を説明変数、知りたい情報を目的変数と呼びます。
回帰には様々な種類が存在し、データの項目数や分布によって使い分ける必要があります。
線形単回帰を解説した記事はこちらになります!
ぜひ見てみてください!
判別ってなに?
判別をざっくり説明すると、複数のグループに分けられているデータを使って未知のデータがどのグループに属すかを予測することです。下の例を見てみましょう。

これは性別、身長、体重のデータです。下に横軸が身長、縦軸が体重の散布図を載せておきます。

これを見ると右上に男性が固まって左下に女性が固まっていますね。つまりこのデータからは身長と体重が大きい人は男性で小さい人は女性であるという傾向が読み取れます。
ここで1つの疑問が生まれます。
身長と体重が分かったら性別を予測できるのかな?
結論できます。
これが判別分析です。男性と女性のように2つのグループのどちらに属すかを予測するのを二値分類と呼びます。一方男性、女性、犬のように3つ以上のグループのどれに属すかを予測するのを多値分類と呼びます。
二値分類について解説した記事はこちらになります!
ぜひこちらも見てみてください!
回帰と判別のちがい
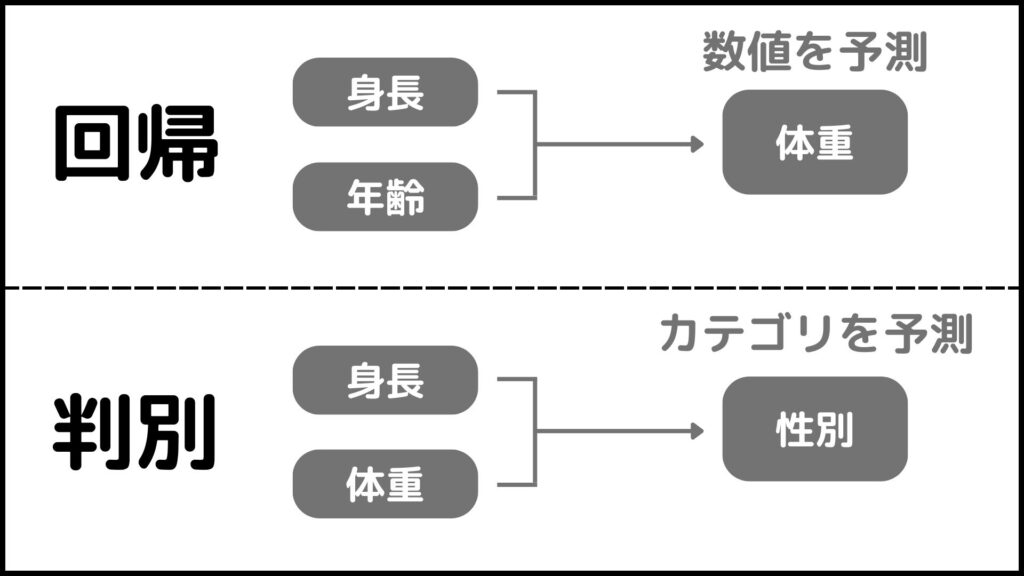
回帰と判別の違いは出力値です。
回帰の出力値は数値
先ほど説明したように、回帰分析では説明変数というデータを入力すると目的変数というデータが出力されるようにしたいのです。ここでの目的変数は数値になります。
例えば身長と年齢を入力すると体重が出力される分析をする場合、出力値の体重は数値です。よってこれは回帰分析になります。
判別の出力値はカテゴリ
こちらも先ほど説明したように、判別分析でも説明変数を入力すると目的変数というデータが出力されるようにしたいのですが、ここでの目的変数はカテゴリになります。
例えば身長と体重を入力すると性別が出力される分析をする場合、出力値の性別はカテゴリです。よってこれは判別分析になります。
カテゴリ ・・・グループのこと
まとめると下の図のようになります。
おわりに
いかがでしたでしょうか。
今回の記事では回帰と判別について説明していきました。
これからもこのようにデータ分析について解説したいと思います。ぼくが一番勉強になるので続けていきたいです!
最後までこの記事を読んでくれてありがとうございました。
この記事が役に立ったら幸いです。





