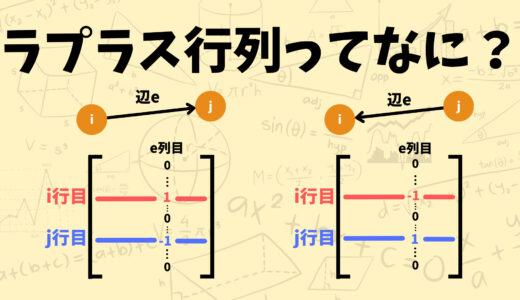
今日やること↓↓↓
割当問題を線形計画問題として定式化:
\(\min \;\;\; \sum\limits_{i \in E, j \in J} w_{ij}x_{ij}\)
\(\;\text{s.t.}\;\;\;\sum\limits_{j \in J} x_{ij}=1 \;\;\;\; (\forall i \in E)\)
\(\;\;\;\;\;\;\;\;\;\sum\limits_{i \in E} x_{ij}=1 \;\;\;\; (\forall j \in J)\)
\(\;\;\;\;\;\;\;\;\; x_{ij} \geq 0 \;\;(\forall i \in E \; \forall j \in J)\)
上の問題の双対問題:
\(\max \;\;\; \sum\limits_{i \in E}d(i) + \sum\limits_{j \in J} d(j)\)
\(\;\text{s.t.}\;\;\;d(i) + d(j) \leq w_{ij} \;\;\;\; (\forall i \in E, \; \forall j \in J)\)
こんにちは!しゅんです!
今回の記事では割当問題ついて解説していきます!
これまでは割当問題を整数計画問題として定式化する方法やハンガリー法などの解説をしましたが、この記事ではちょっと視点を変えて線形計画問題として定式化された割当問題の双対問題について話していきたいと思います!
割当問題が何なのかについてはこちらの記事で解説しています!
割当問題をハンガリー法で解く方法についてはこちらの記事で解説しています!
それではやっていきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
今回使う具体例
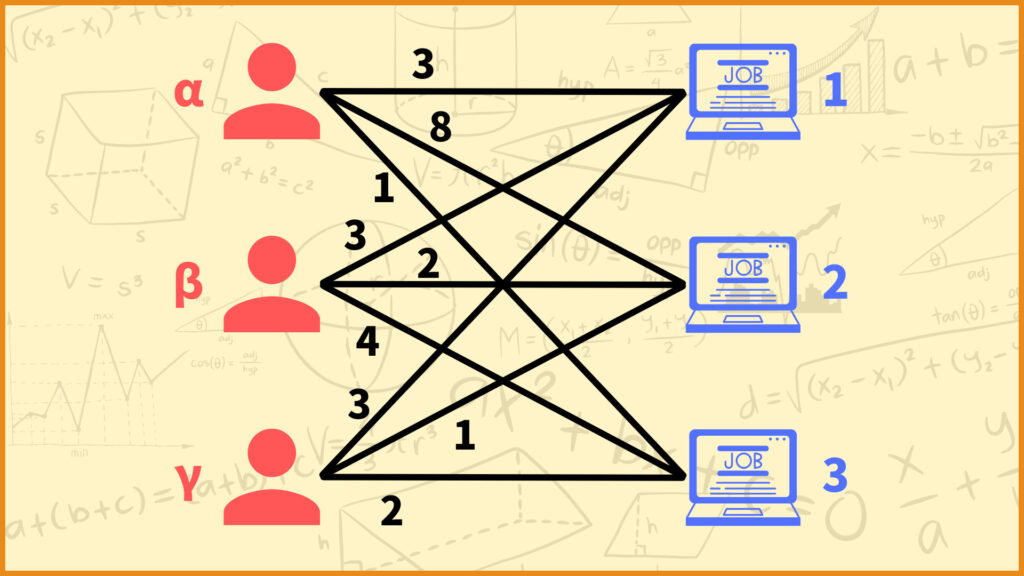
今回は3人の従業員\(\alpha,\beta,\gamma\)を3つの仕事\(1,2,3\)に割り当てる問題を考えていきます。1人の従業員が1つの仕事を担当し、どの仕事も1人の従業員によって行われると仮定します。従業員と仕事を結ぶ辺の上に書いてあるのが辺の重みです。
目的は重みの合計が最小となる割当を見つけることです。
割当問題を線形計画問題として定式化する
双対問題を考えるために、まず割当問題を線形計画問題として定式化しましょう。
パラメータ:
\(E = \{\alpha,\beta,\gamma\}\):従業員の集合
\(J = \{1,2,3\}\):仕事の集合
\(w_{ij}\):辺\((i,j)\)の重み
変数:
\(x_{ij}\):辺\((i,j)\)を採用するなら1、そうじゃないなら0
線形計画問題として定式化:
\(\min \;\;\; \sum\limits_{i \in E, j \in J} w_{ij}x_{ij}\)
\(\;\text{s.t.}\;\;\;\sum\limits_{j \in J} x_{ij}=1 \;\;\;\; (\forall i \in E)\)
\(\;\;\;\;\;\;\;\;\;\sum\limits_{i \in E} x_{ij}=1 \;\;\;\; (\forall j \in J)\)
\(\;\;\;\;\;\;\;\;\; x_{ij} \geq 0 \;\;(\forall i \in E \; \forall j \in J)\)
前回の記事では割当問題を整数計画問題として定式化したので、\(x_{ij} \in \{0,1\}\)でしたが、今回は線形計画問題として定式化したいので\(x_{ij} \geq 0\)になっています。
「0か1しか取れない」から「0以上の任意の実数を取れる」と言う風に条件を緩和することを線形緩和と言ったりします。一般に緩和問題の最適値と元の問題の最適値は異なります。
しかし今回考えている割当問題については、実は線形緩和しても元の問題と同じ答えが得られるんです。これは制約条件の係数行列が完全単模行列(totally unimodular matrix)だからです。
双対問題を導出する
それでは実際に双対問題を導出してみましょう。
導出したい双対問題:
\(\max \;\;\; \sum\limits_{i \in E}d(i) + \sum\limits_{j \in J} d(j)\)
\(\;\text{s.t.}\;\;\;d(i) + d(j) \leq w_{ij} \;\;\;\; (\forall i \in E, \; \forall j \in J)\)
標準形の線形計画問題の双対問題をおさらいする
まず最初に標準形の線形計画問題の双対問題をおさらいしましょう。なぜ標準形を考えるかと言うと、今回の割当問題が標準形の線形計画問題だからです。
標準形の線形計画問題:
\(\min \;\;\; c^\top x\)
\(\;\text{s.t.}\;\;\;Ax=b \)
\(\;\;\;\;\;\;\;\;\; x \geq 0\)
双対問題:
\(\max \;\;\; b^\top y\)
\(\;\text{s.t.}\;\;\;A^\top y \leq c \)
つまり\(A,b,c\)が分かってしまえば機械的に双対問題を作ることができるという訳です。
割当問題の線形計画問題を1つずつ書く
ということで割当問題の線形計画問題に関して\(A,b,c\)を求めてみましょう。とは言ってもこのままでは分かりにくいので、1つずつ書いて理解していこうと思います。
目的関数
割当問題の目的関数:
\(\sum\limits_{i \in E, j \in J} w_{ij}x_{ij}\)
\(\sum\)を使わずに書いてみましょう。
割当問題の目的関数(\(\sum\)を使わずに書く):
\(w_{\alpha 1}x_{\alpha 1} + w_{\alpha 2}x_{\alpha 2} + w_{\alpha 3}x_{\alpha 3}\)
\(+w_{\beta 1}x_{\beta 1} + w_{\beta 2}x_{\beta 2} +w_{\beta 3}x_{\beta 3}\)
\(+w_{\gamma 1}x_{\gamma 1}+w_{\gamma 2}x_{\gamma 2}+w_{\gamma 3}x_{\gamma 3}\)
これを見ると、
\(c = \begin{pmatrix} w_{\alpha 1} \\ w_{\alpha 2} \\ w_{\alpha 3} \\ w_{\beta 1} \\ w_{\beta 2} \\ w_{\beta 3} \\ w_{\gamma 1} \\ w_{\gamma 2} \\ w_{\gamma 3} \end{pmatrix}, \;\; x = \begin{pmatrix} x_{\alpha 1} \\ x_{\alpha 2} \\ x_{\alpha 3} \\ x_{\beta 1} \\ x_{\beta 2} \\ x_{\beta 3} \\ x_{\gamma 1} \\ x_{\gamma 2} \\ x_{\gamma 3} \end{pmatrix} \)
とすれば\(c^\top x\)で目的関数を表すことができますね。
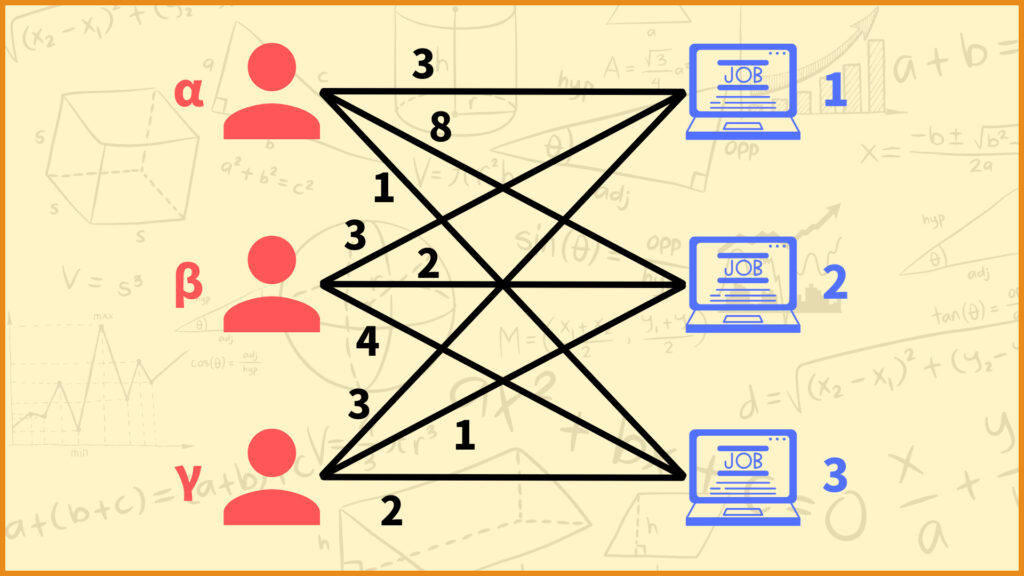
上の辺の重みの例で言うと
\(c = \begin{pmatrix} 3 \\ 8 \\ 1 \\ 3 \\ 2 \\ 4 \\ 3 \\ 1 \\ 2 \end{pmatrix}\)
となります。
制約条件
割当問題の制約条件:
\(\sum\limits_{j \in J} x_{ij}=1 \;\;\;\; (\forall i \in E)\)
\(\sum\limits_{i \in E} x_{ij}=1 \;\;\;\; (\forall j \in J)\)
\(\sum\)を使わずに書いてみましょう。
割当問題の目的関数(\(\sum\)を使わずに書く):
\(x_{\alpha 1} + x_{\alpha 2} + x_{\alpha 3} = 1\)
\(x_{\beta 1} + x_{\beta 2} + x_{\beta 3} = 1\)
\(x_{\gamma 1} + x_{\gamma 2} + x_{\gamma 3} = 1\)
\(x_{\alpha 1} + x_{\beta 1} + x_{\gamma 1} = 1\)
\(x_{\alpha 2} + x_{\beta 2} + x_{\gamma 2} = 1\)
\(x_{\alpha 3} + x_{\beta 3} + x_{\gamma 3} = 1\)
この制約条件を\(Ax = b\)の形にすることを考えます。目的関数の所で
\(x = \begin{pmatrix} x_{\alpha 1} \\ x_{\alpha 2} \\ x_{\alpha 3} \\ x_{\beta 1} \\ x_{\beta 2} \\ x_{\beta 3} \\ x_{\gamma 1} \\ x_{\gamma 2} \\ x_{\gamma 3} \end{pmatrix} \)
としたので、これに合わせるように係数行列\(A\)を求めてみましょう。
\(A=\begin{pmatrix} 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 \\ 1 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 1 \end{pmatrix}, \;\; b = \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{pmatrix}\)
こうすることで制約条件を\(Ax = b\)の形で表すことができます。
\(A=\begin{pmatrix} 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 \\ 1 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 1 \end{pmatrix}, \;\; b = \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{pmatrix}, c = \begin{pmatrix} w_{\alpha 1} \\ w_{\alpha 2} \\ w_{\alpha 3} \\ w_{\beta 1} \\ w_{\beta 2} \\ w_{\beta 3} \\ w_{\gamma 1} \\ w_{\gamma 2} \\ w_{\gamma 3} \end{pmatrix}\)
\begin{pmatrix} 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 \\ 1 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 1 \end{pmatrix}
この係数行列\(A\)は接続行列と呼ばれます。接続行列の\((i,j)\)成分は頂点\(i\)と辺\(j\)が接続しているか(くっついているか)を表します。詳しいことは下の記事で解説しています!
双対問題を作ってみる
それではさっき求めた\(A,b,c\)を使って双対問題を作ってみましょう。これも目的関数、制約条件に分けてそれぞれ説明していきます。
目的関数
双対問題の目的関数:
\( b^\top y\)
\(b\)はさっき求めた
\(b = \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{pmatrix}\)
を使います。これに合わせるために\(y\)は6次元の列ベクトルにします。
ここでちょっと6次元の6と言う数字に着目してみましょう。
なぜ今回\(y\)が6次元になるかというと、頂点数が6個だからです。というのも列ベクトル\(y\)が6次元なのは、\(b\)が6次元の列ベクトルだからです。
さらに振り返ってみると、\(b\)が6次元の列ベクトルなのは制約条件が6本だからです。割当問題の制約条件は何を表しているのかを思い出すと、「各頂点に関して、その頂点に接続する辺から1本だけ選べる」というのが割当問題の制約条件でした。つまり頂点の数と制約条件の本数が一致します。
以上のことを踏まえると、変数ベクトル\(y\)は各頂点に関する何かしらの変数という風に考えることができます。
ということで変数ベクトル\(y\)の成分は\(d(i) \; (\forall i \in E)\) と \( d(j) \; (\forall j \in J)\) としてみましょう。
\(y = \begin{pmatrix} d(\alpha) \\ d(\beta) \\ d(\gamma) \\ d(1) \\ d(2) \\ d(3) \end{pmatrix}\)
これら\(b,y\)を使って目的関数を書いてみましょう。
双対問題の目的関数:
\( b^\top y = d(\alpha)+d(\beta)+d(\gamma)+d(1)+d(2)+d(3)\)
\(= \sum\limits_{i \in E} d(i) + \sum\limits_{j \in J} d(j)\)
制約条件
双対問題の制約条件:
\(A^\top y \leq c \)
先ほど求めた\(A\)の転置\(A^\top\)は以下のようになります。
\(A^\top=\begin{pmatrix} 1 & 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 1 \end{pmatrix}\)
次にこの\(A^\top\)と\(y\)の積を考えます。
\(A^\top y=\begin{pmatrix} 1 & 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} d(\alpha) \\ d(\beta) \\ d(\gamma) \\ d(1) \\ d(2) \\ d(3) \end{pmatrix} = \begin{pmatrix} d(\alpha) + d(1) \\ d(\alpha)+d(2) \\ d(\alpha)+d(3) \\ d(\beta) + d(1) \\ d(\beta) + d(2) \\ d(\beta) + d(3) \\ d(\gamma) + d(1) \\ d(\gamma) + d(2) \\ d(\gamma) + d(3) \end{pmatrix}\)
また、
\(c = \begin{pmatrix} w_{\alpha 1} \\ w_{\alpha 2} \\ w_{\alpha 3} \\ w_{\beta 1} \\ w_{\beta 2} \\ w_{\beta 3} \\ w_{\gamma 1} \\ w_{\gamma 2} \\ w_{\gamma 3} \end{pmatrix}\)
なので、\(A^\top y \leq c\)は
\(d(\alpha) + d(1) \leq w_{\alpha 1}\)
\(d(\alpha) + d(2) \leq w_{\alpha 2}\)
\(d(\alpha) + d(3) \leq w_{\alpha 3}\)
\(d(\beta) + d(1) \leq w_{\beta 1}\)
\(d(\beta) + d(2) \leq w_{\beta 2}\)
\(d(\beta) + d(3) \leq w_{\beta 3}\)
\(d(\gamma) + d(1) \leq w_{\gamma 1}\)
\(d(\gamma) + d(2) \leq w_{\gamma 2}\)
\(d(\gamma) + d(3) \leq w_{\gamma 3}\)
となります。なんかめっちゃ綺麗ですね。
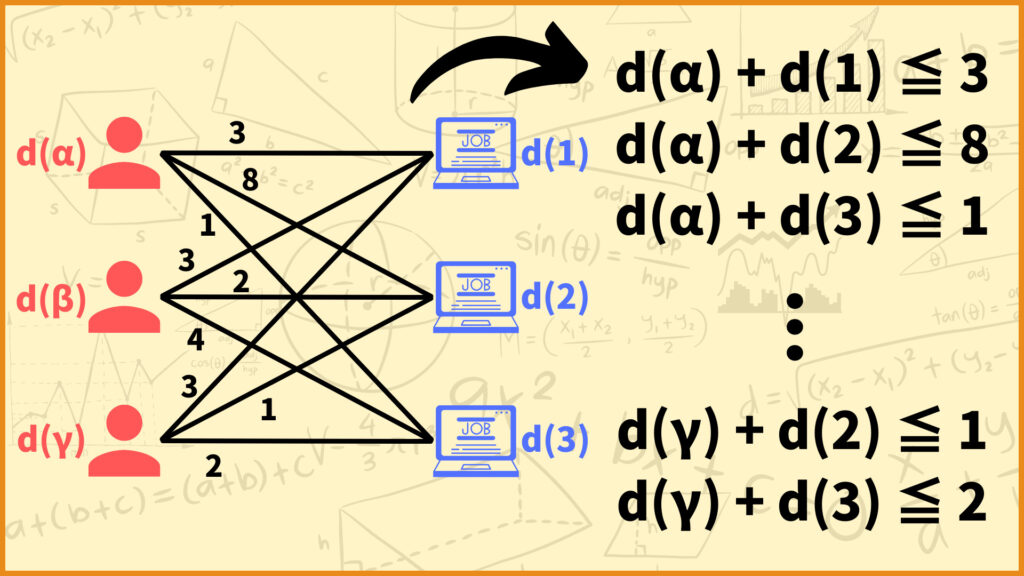
上の式を簡潔に表すと以下のようになります。
\(d(i)+d(j) \leq w_{ij} \;\; (\forall i \in E,\forall j \in J)\)
目的関数と制約条件を合わせる
ということで目的関数と制約条件を合わせて書くことで、導出したかった双対問題が得られます。
導出したかった双対問題:
\(\max \;\;\; \sum\limits_{i \in E}d(i) + \sum\limits_{j \in J} d(j)\)
\(\;\text{s.t.}\;\;\;d(i) + d(j) \leq w_{ij} \;\;\;\; (\forall i \in E, \; \forall j \in J)\)
おわりに
いかがでしたか。
今回の記事では割当問題と双対問題について解説していきました。
今後もこのような組合せ最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。